
上浒文通大 SHANGHAI JIAO TONG UNIVERSITY 积分变换 第七章 Fourier变换 1.Fourier积分 大 溷 2.Fourier?变换 Ww 奥 3.广义Fourier?变换 4.Fourier变换的性质 SHAN ERS
积分变换 第七章 Fourier 变换 1. Fourier积分 2. Fourier变换 3. 广义Fourier变换 4. Fourier变换的性质

上游充通大学 SHANGHAI JIAO TONG UNIVERSITY Fourier口▣ ● 176800口▣▣ ● 18070▣▣“000▣ 0▣000000口0 0口00 99 ● 1822☐▣▣“ 0000 66 00000000 99
Fourier生 平 • 1768年 生 于法国 • 1807年提出 “ 任何周期 信号都可用正弦函数的 级数表示 ” • 1822年发表 “ 热的分析 理论 ” ,首次提出 “ 任 何非周期信号都可用正 弦函数的积分表示

上海气通大粤 SHANGHAI JIAO TONG UNIVERSITY §1 Fourier积分 1.1 Fourier级数 具有性质f(什T=f(),其中T称作周期 t 最常用的一种周期函数是三角函数 f)=Asin(ot+),其中0F2dT Asin(wi+j)=asinwi+bcoswt. 3
3 具有性质fT(t+T)=fT(t), 其中T称作周期. 1.1 Fourier 级数 §1 Fourier积分 t 最常用的一种周期函数是三角函数 fT(t)=Asin(ωt+j), 其中ω=2π/T. Asin(wt+j)=asinwt+bcoswt
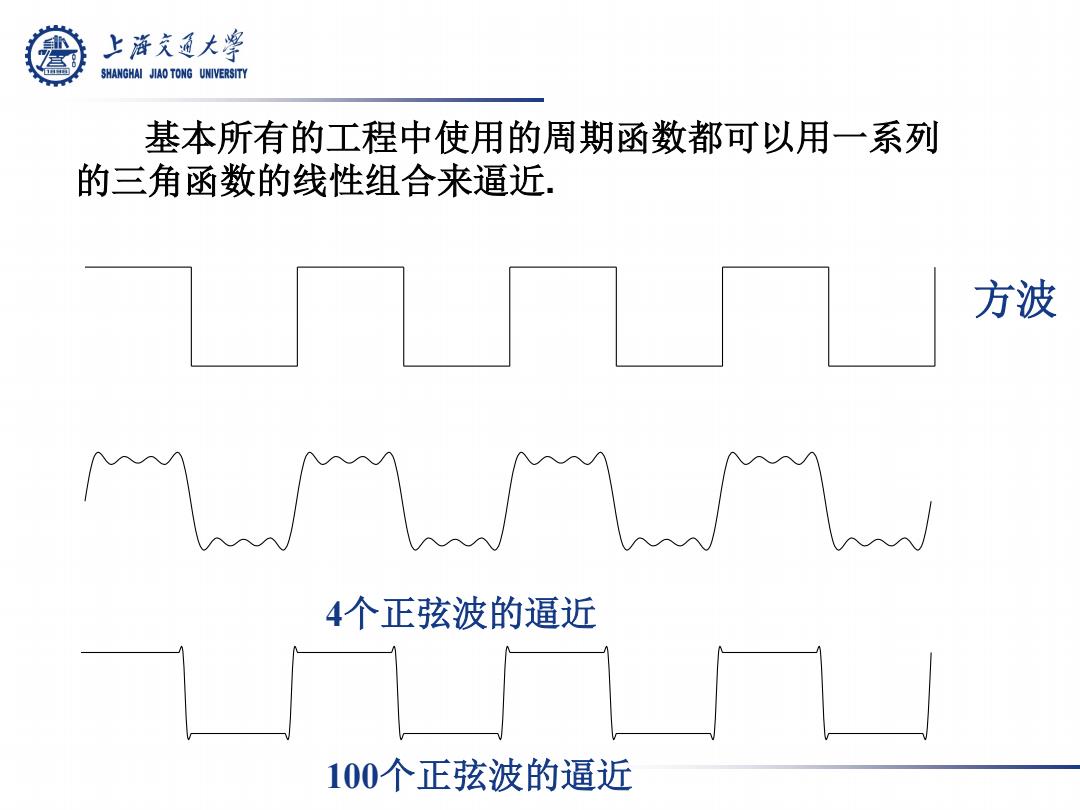
上降充通大 SHANGHAI JIAO TONG UNIVERSITY 基本所有的工程中使用的周期函数都可以用一系列 的三角函数的线性组合来逼近 方波 4个正弦波的逼近 100个正弦波的逼近
基本所有的工程中使用的周期函数都可以用一系列 的三角函数的线性组合来逼近. 方波 4个正弦波的逼近 100个正弦波的逼近

上游充通大学 SHANGHAI JIAO TONG UNIVERSKY 设)以T为周期,称在[-T12,T12]内满足 Dirichlet条件: (1)ft)连续或只有有限个第一类间断点; (2)()至多只有有限个极值点。 第一类间断点
(1)f(t)连续或只有有限个第一类间断点; (2)f(t)至多只有有限个极值点。 Dirichlet条件: 设f(t)以T为周期,称在[-T/2,T/2] 内满足 第一类间断点