
上游哀通大 SHANGHAI JIAO TONG UNIVERSITY 第二章分离变量法 §10.2一维热传导方程 漏 上海交通大学数学系 n 唐异垒 SHAN
第二章 分离变量法 上海交通大学数学系 唐异垒 §10.2 一维热传导方程

上游充大学 SHANGHAI JIAO TONG UNIVERSITY §10.2一维热传导方程 类齐次边界条件(两端温度恒定)的定解问题 8t a,1>0,0<r<L (1) u(0,t)=0,u(L,t)=0, u(x,0)=(x) u(x,t)=X(x)T(t)代入PDE和边界条件, XT-a2X"T=0; T'(t) X"(x) - X(O)T(t)=X(L)T(t)=0 a2T(t) X(x) X"+2X=0,(0<x<L) →固有问题 (2) X(0)=X(L)=0 T'+a2T=0,(3)
2 2 2 ( ) , 0, 0 I (1) (0, ) 0, ( , ) 0, ( ,0) ( ) u u a t xL t x u t uLt ux x φ ∂ ∂ = > << ∂ ∂ = = = 类齐次边界条件 两端温度恒定 的定解问题 (I) §10.2 一维热传导方程 u xt X xT t ( ,) ( ) () = 代入PDE和边界条件, 2 0; (0) ( ) ( ) ( ) 0 XT a X T X T t X LT t ′ ′′ − = = = 2 () ( ) () ( ) Tt X x aT t X x λ ′ ′′ ⇒ = =− 0, (0 ) 2 (0) ( ) 0 X X xL X XL ′′ + = << λ ⇒ = = 固有问题 ( ) 2 T aT ′ + = λ 0, (3)

上游充通大粤 SHANGHAI JIAO TONG UNIVERSITY 四>固有问题 X"+几X=0,(0<x<L) (2) X(0)=X(L)=0 k2π2 固有值 入== (k=1,23.…) (2≤0只有零解) 固有函数 kπ X(x)=Ck sin (k=1,2,L) T'+a2T=0,(3)→ 0=Rp21 (k=1,2,L)
(II) 固有问题 X ′′ + λX = 0, (0 < x < L) X (0) = X (L) = 0 固有值 固有函数 2 0, (3) TaT λk ′ +=⇒ 2 2 2 , ( 1 2,3...) k k k , L π λ λ = = = ( ) sin , ( 1, 2, ) k k k Xx C x k L π = = L 2 ( ) exp ( ) , ( 1, 2, ) k k k a Tt B t k L π =− = L ( 0 .) λ ≤ 只有零解 (2)

上游充通大 SHANGHAI JIAO TONG UNIVERSITY 特解的叠加 u(x,t)=∑Xx(x)Tk(t) k=1 =24e kπ sin X k=1 L 再由初始条件(x)=ux,0)=∑4,sn kπ k=1 4=20xsn经d血 kπ
(III) 特解的叠加 sin ( , ) ( ) ( ) 1 1 2 ∑ ∑ ∞ = − ∞ = = = k t L k a k k k k x L k A e u x t X x T t π π 1 ( ) ( ,0) sin k k k x ux A x L π φ ∞ = 再由初始条件 = = ∑ 0 2 ( )sin d . L k k A x xx L L π = φ ∫
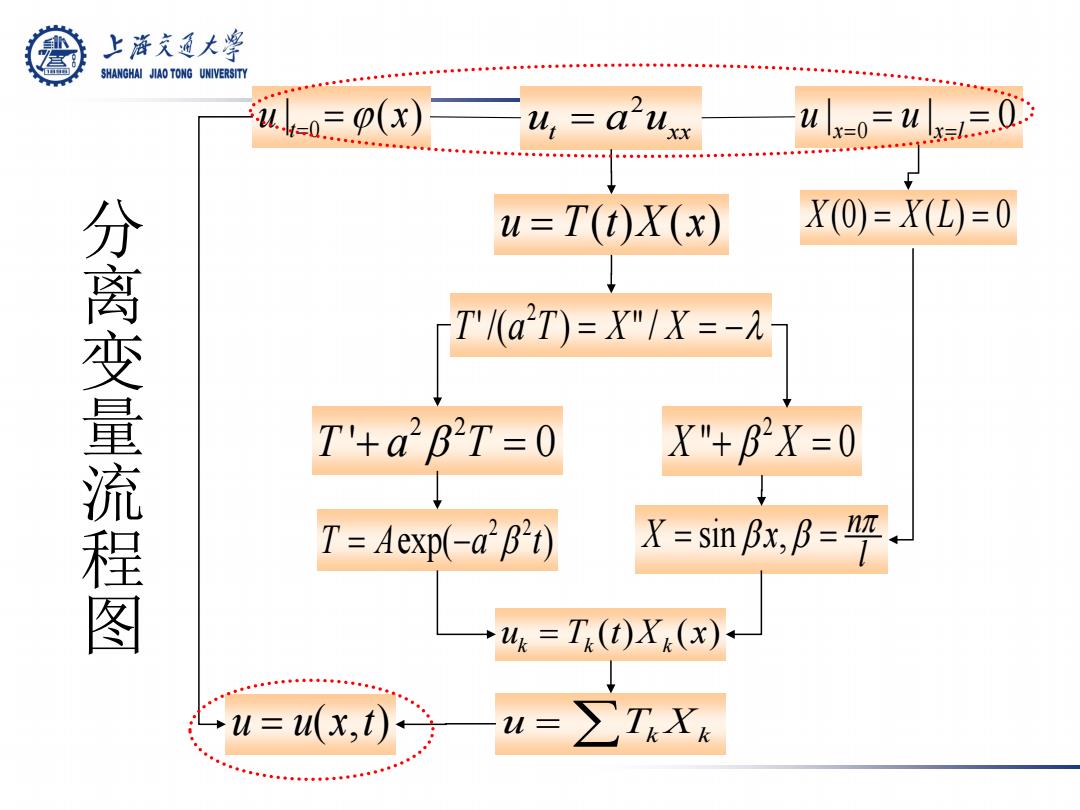
上游充通大 SHANGHAI JIAO TONG UNIVERSITY u三p(x) u,a'uxx ulx=o=u 0. u=T(t)X(x) X(0)=X(L)=0 分离变量流程图 T1a2T)=X"1X=-元 T'+a2B2T=0 X"+B2X=0 T=Aexp(-a"B"t) X=sin Bx,.B=℉ 4=T(0X(x u=u(x,t) u=∑TXx
ut a uxx 2 = 0 | |0 x xl u u u | t=0= ϕ(x) = = = = u = T(t)X (x) X (0) = X (L) = 0 T'/(a T ) = X" / X = −λ 2 2 2 Ta T ' 0 + = β 2 X X " 0 + = β 2 2 TA a t = − exp( ) β sin , n l X x π = = β β u T (t)X (x) k = k k ) u = ∑Tk Xk u = u(x,t 分离变量流程图