
第三节平面及其方程设一平面通过已知点M。(xo,Jo,zo)且垂直于非零向量 n=(A,B,C),求该平面IⅡ的方程ZMo.任取点 M(x,y,z)e II,则有1M.M In.故 M.M·n=0,+MoM = (x-xo,y-yo,z-zo)A(x-xo)+B(y-y)+C(z-z)=0上式称为平面Ⅱ的点法式方程,称n为平面的法向量返回MathGS公式上页下页线与面数学家
第三节 平面及其方程 x y z ( , , ) 0 0 0 0 设一平面通过已知点 M x y z 且垂直于非零向 ( ) ( ) ( ) 0 . A x − x0 + B y − y0 +C z − z0 = 上式称为平面 的点法式方程, 求该平面 的方程. M (x, y,z) Π , 称n为平面的法向量. 量 n = (A , B, C), . M0 M ⊥n 0 , M0 M n = 则有 故 任取点 M0 M n
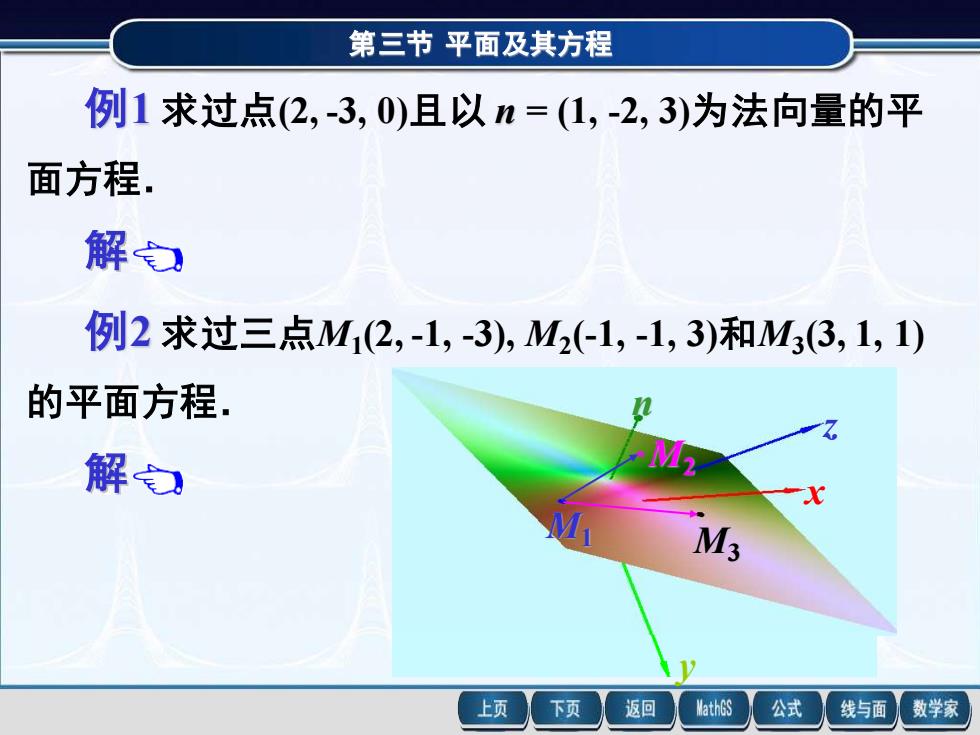
第三节平面及其方程例1 求过点(2,-3, 0)且以 n =(1,-2, 3)为法向量的平面方程,解包例2 求过三点M,(2,-1, -3), M2(-1, -1, 3)和M3(3, 1, 1)的平面方程,M2解包MIM3P返回MathGS公式上页下页线与面数学家
第三节 平面及其方程 M1 M2 M3 x y z n 例1 求过点(2, -3, 0)且以 n = (1, -2, 3)为法向量的平 面方程. 第三节 平面及其方程 x y z O n 例1 求过点(2, -3, 0)且以 n = (1, -2, 3)为法向量的平 面方程. 解 由点法式方程,得所求平面的方程为 1·(x – 2) –2(y + 3) + 3(z – 0) = 0, 即 x – 2y + 3z – 8 = 0. 例2 求过三点M1 (2, -1, -3), M2 (-1, -1, 3)和M3 (3, 1, 1) 的平面方程. 第三节 平面及其方程 M1 M2 M3 x y z n 解 先求平面的法向量n. 例2 求过三点M1 (2, -1, -3), M2 (-1, -1, 3)和M3 (3, 1, 1) 的平面方程. 由于 , , n ⊥ M1 M2 n ⊥ M1 M3 故可取 . n = M1 M2 M1 M3 而 ( 3 , 0 , 6) , (1, 2 , 4) , M1 M2 = − M1 M3 = 故 12 18 6 . 1 2 4 1 2 1 3 3 0 6 i j k i j k n = M M M M = − = − + −
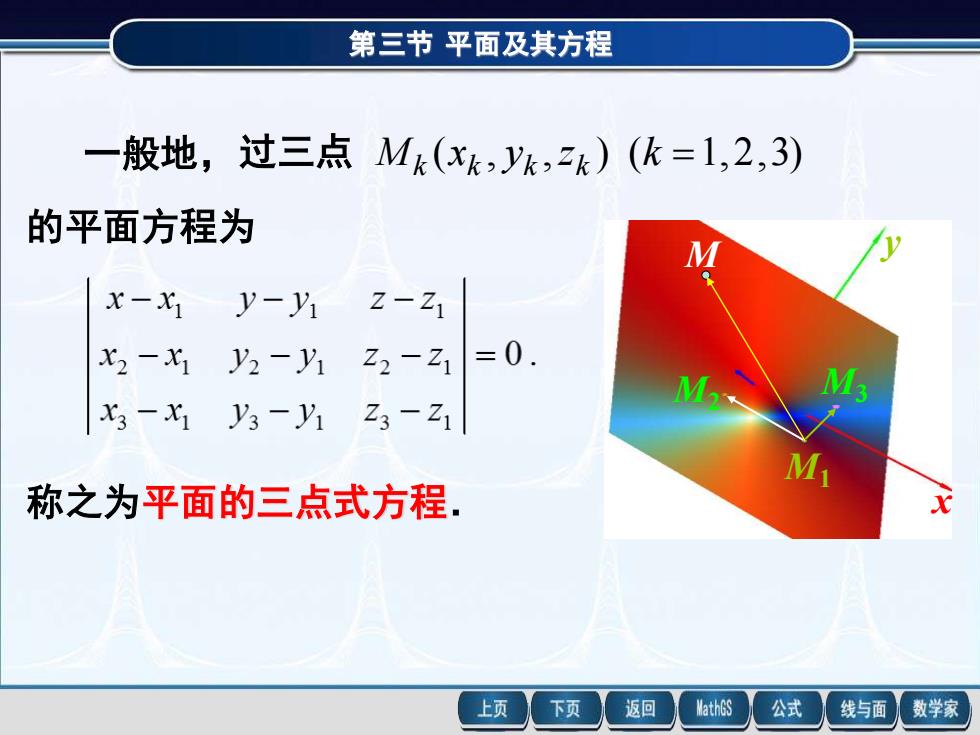
第三节 平面及其方程一般地,过三点 Mk(xk,k,z)(k=1,2,3)的平面方程为Mx-xi7y-yi=0.x2 -xiZ2 - Z1y2 -yiMM.X3 -XiZ3 - Z1V3-yiMx称之为平面的三点式方程返回MathGS公式上页下页线与面数学家
第三节 平面及其方程 一般地,过三点 M (x , y ,z ) (k =1,2,3) k k k k 的平面方程为 称之为平面的三点式方程. M1 M2 M3 M x y
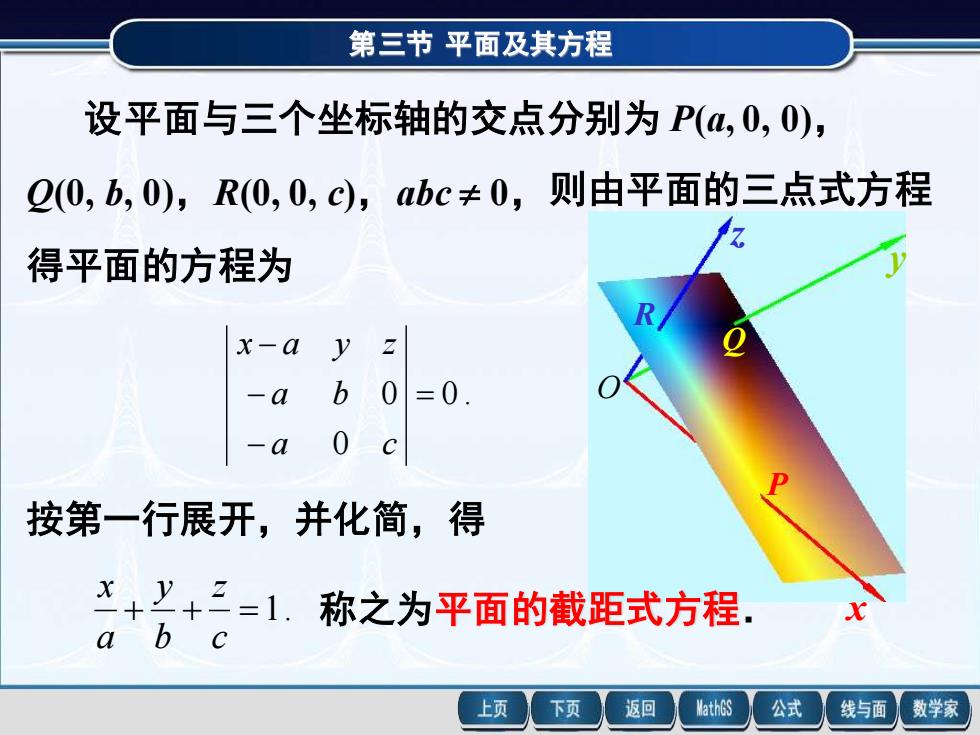
第三节平面及其方程设平面与三个坐标轴的交点分别为P(a,0,0)Q(0,b,0),R(0,0,c), abc≠0,则由平面的三点式方程得平面的方程为RQyLX一ab0=0a0Ca按第一行展开,并化简,得X+二+==1.称之为平面的截距式方程baC上页下页返回MathGS公式数学家线与面
第三节 平面及其方程 P Q R x y z O 设平面与三个坐标轴的交点分别为 P(a, 0, 0), Q(0, b, 0),R(0, 0, c),abc 0, 得平面的方程为 0 . 0 0 = − − − a c a b x a y z 按第一行展开,并化简,得 + + =1. c z b y a x 称之为平面的截距式方程. 则由平面的三点式方程