
定义2.f(x)在区间I上的原函数全体称为f(x)在I 上的不定积分,记作f(x)dx,其中 ∫一积分号;f()一被积函数; x一积分变量;f(x)d一被积表达式, 若F'(x)=f(x),则 「f(x)dr=F(x)+C(C为任意常数) 例如, 「e'dx=ex+C C称为积分常数 ∫x2dr=}x3+C 不可丢! sin xdx=-cos x+C
山东农业大学 高等数学 主讲人:苏本堂 定义 2. 在区间 I 上的原函数全体称为 上的不定积分, 其中 — 积分号; — 被积函数; — 积分变量; — 被积表达式. 若 则 ( C 为任意常数 ) C 称为积分常数 不可丢 ! 例如, = e x x d e C x + = x dx 2 x +C 3 3 1 = sin xdx − cos x +C 记作
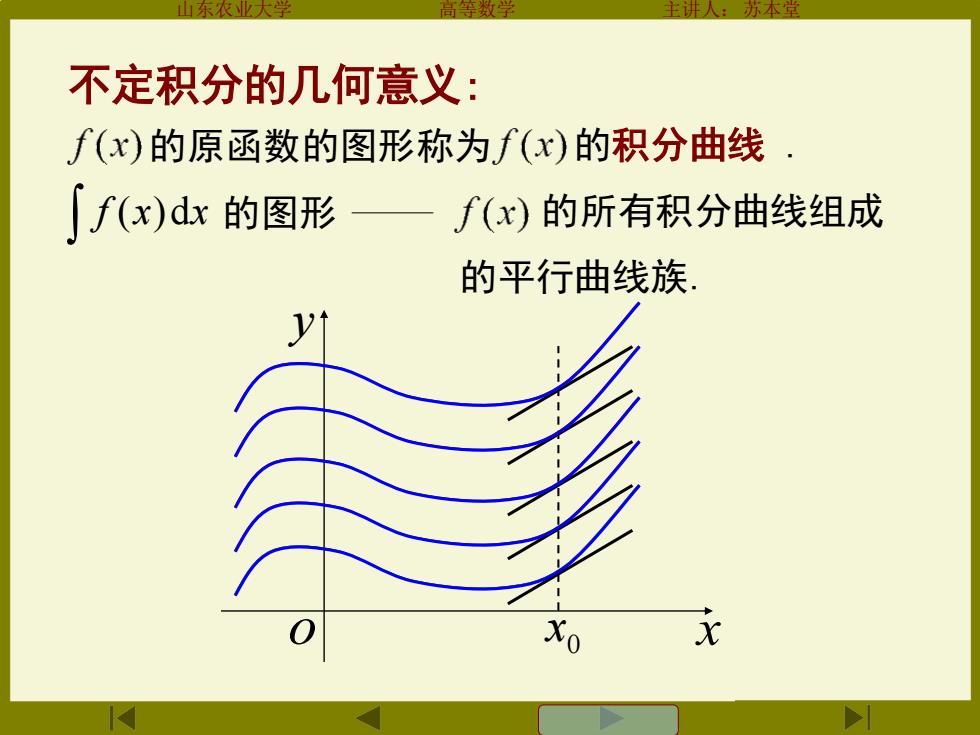
不定积分的几何意义: ∫(x)的原函数的图形称为f(x)的积分曲线· ∫f(x)dx的图形 f(x)的所有积分曲线组成 的平行曲线族 Xo
山东农业大学 高等数学 主讲人:苏本堂 不定积分的几何意义: 的原函数的图形称为 f (x)dx 的图形 的所有积分曲线组成 的平行曲线族. y o x0 x 的积分曲线