《高等数学》课程教学资源（课件讲稿）第十二章 级数_1202常数项级数的审敛法

nD的收敛性。例 2判别正项级数+1n=in7n"-，而收敛，则2收敛解：un+1n=ln例3 判别下列级数的收敛性：(1) ZZ(2)?5h.2nn(n2X11而之收敛.则收敛，(1)un解3n(n2 +1)n(n2 + 1)1=11n=12，而之收(2)u. = n.2"则之收敛，贝收敛一n.2=1oo8个个个高等数学教学部不不不

高等数学教学部 6 1 3   n n  un 3 n n  , 1 2 n  ( 1) 1 (1) 2   n n un , 1 2 3 n  n n n u 2 1 (2)   , 2 1 n 

定理3（比较审敛法的极限形式）设u,和v,是两个正项级数，-1n=1un=l. (1) 当0 <l < +o0时,Zv,和u,收敛性相同;(2) 当I-0时,且lim1->001n=1n=1若v,收敛，则u,收敛；(3）当l=+时，若,发散，则u,发散n=1n=1nsn=un=l, 则对于&=证 (1)因lim存在正整数 N，当n> N时2n>001un.n.cu.nunn-l<8,有即Vn若Z,收敛，而u,,w,，则≥u,收敛，n=1n=*2、,发数。而小,儿,发胶之和,收微性相间若n=1n=I=0008个个高等教学教学部不个

高等数学教学部 7

?"=0,则对于ε=1,存在正整数 N，当n>N时,因lim(2)n->00Vn有|",-1k1, 则"n<1, u, <vr.若v,收敛，而u,<v,，则u,收敛.n=1n=lun = +o0,则lim n =0,因lim(3)n>01n-0un8080Z推收敛，u,收敛可推由(2)知,n=1n=180Zi则当，发散时，可推u,必发散n=1n=18008个个个高等数学教学部不不不

高等数学教学部 8

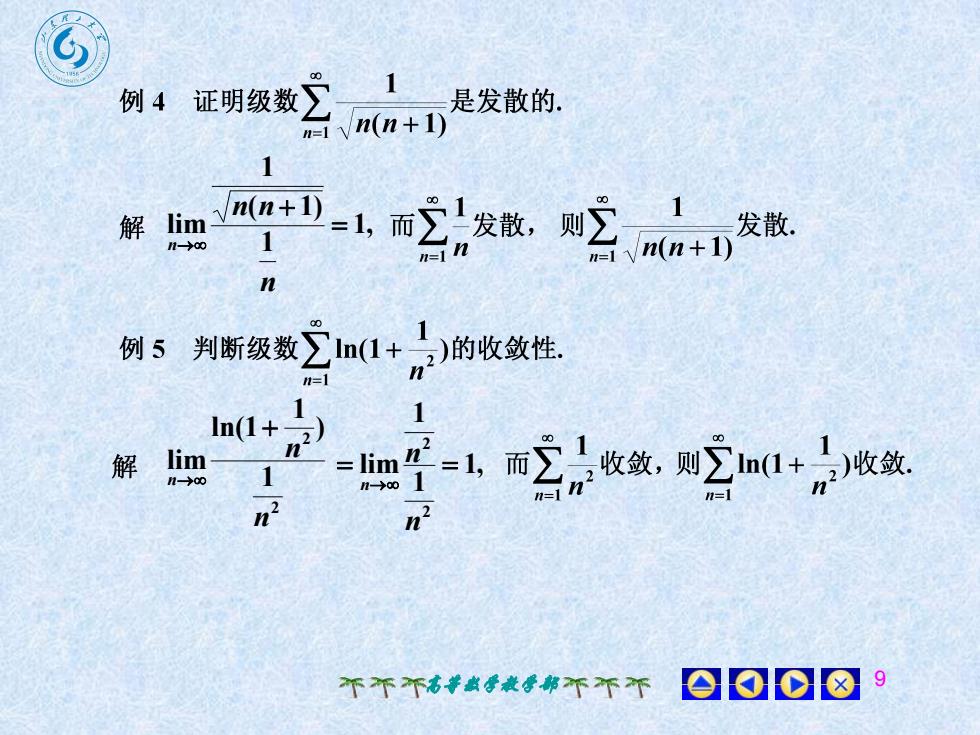
:是发散的例 4 证明级数n(n+ 1)n=1 Vn(n+1)=1,而 发散，则lim发散解11-00(n(n+1)=in11n00in(1+例 5判断级数，)的收敛性nn=111In(1 +80n2Zlim收敛，则In(1+)收敛而= lim解=1,11n-00n-00nn=11=nn00108个个个高等数学教学部个不个

高等数学教学部 9 1, 1 ( 1) 1 lim    n n n n 2 2 1 ) 1 ln(1 lim n n n   1, 1 1 lim 2 2    n n n

Z(1-cos );(2) Z3例6判断下列级数的收敛性：（1）13"_2nn=1111-cos2n?n= lim而之早(1)lim解收敛,则之(1-cos-)收敛.12,11-00n->00nnn=1n=1n?180.3" -2"NZ收敛lim收敛，则而=(2) lim12n3″n-00n=13"n->00n=13n00810个个个高等数学教学部不不个

高等数学教学部 10 2 1 1 1 cos (1)lim n n n   , 2 1 1 2 1 lim 2 2    n n n n n n n 3 1 3 2 1 (2)lim   n n ) 3 2 1 ( 1 lim     1