
第四节 区间估计 一、区间估计的基本概念 二、典型例题 三、小结
第四节 区间估计 一、区间估计的基本概念 二、典型例题 三、小结

、 区间估计的基本概念 1.置信区间的定义 设总体X的分布函数F(x9)含有一个未知参 数g,对于给定值a(0<a<1),若由样本X1,X2,L, X,确定的两个统计量 q=q(X1,X2,L,Xm)和4=q(X1,X2,L,Xm)满足 P{q(X1,X2,L,Xm)<9<q(X1,X2,L,Xn)}=1-M, 则称随机区间(g,9)是q的置信度为1-a的置信区 间,q和q分别称为置信度为1-a的双侧置信区间 的置信下限和置信上限,1-a为置信度
一、区间估计的基本概念 1. 置信区间的定义

关于定义的说明 被估计的参数g虽然未知,但它是一个常数, 没有随机性,而区间(g,4)是随机的. 因此定义中下表达式 Pig(X,X2,L,X)<q<q(X,X2L,X)=1-a 的本质是: 随机区间g,q)以1-a的概率包含着参数q的真值, 而不能说参数g以1-a的概率落入随机区间g,9)
关于定义的说明
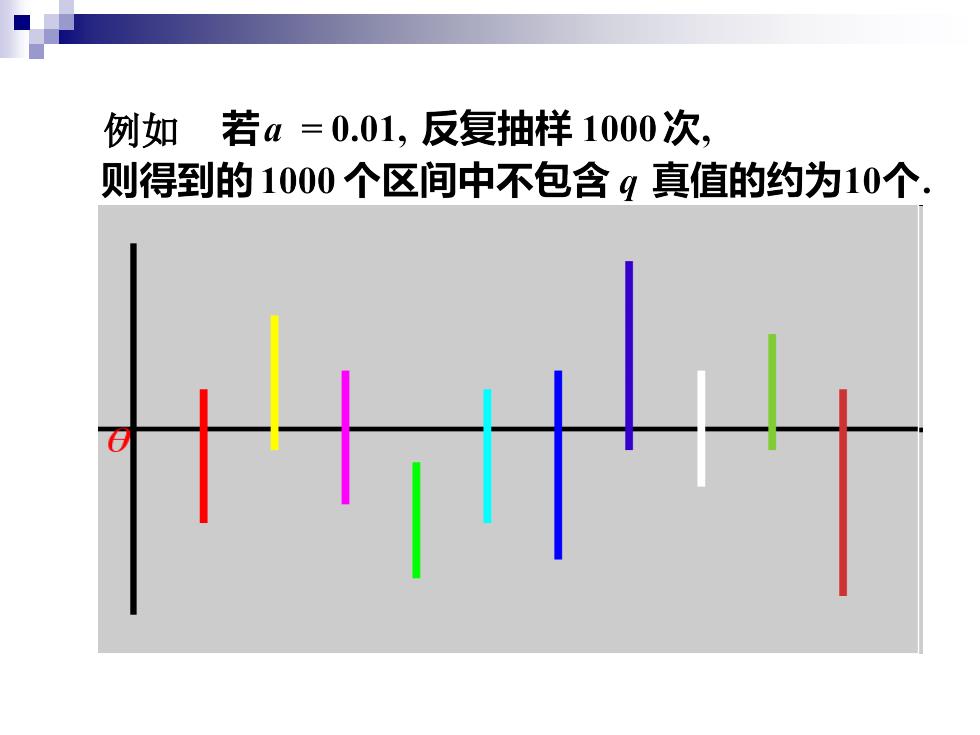
例如 若a=0.01,反复抽样1000次, 则得到的1000个区间中不包含g真值的约为10个
例如

2.求置信区间的一般步骤(共3步) (1)寻求一个样本X,X,L,X,的函数: Z=Z(X,X2L ,Xq) 其中仅包含待估参数g,并且Z的分布已知 且不依赖于任何未知参数(包括q). (2)对于给定的置信度1-a,定出两个常数,b, Pfa<Z(X,X2,L,Xiq)<b=1-a
2. 求置信区间的一般步骤(共3步)