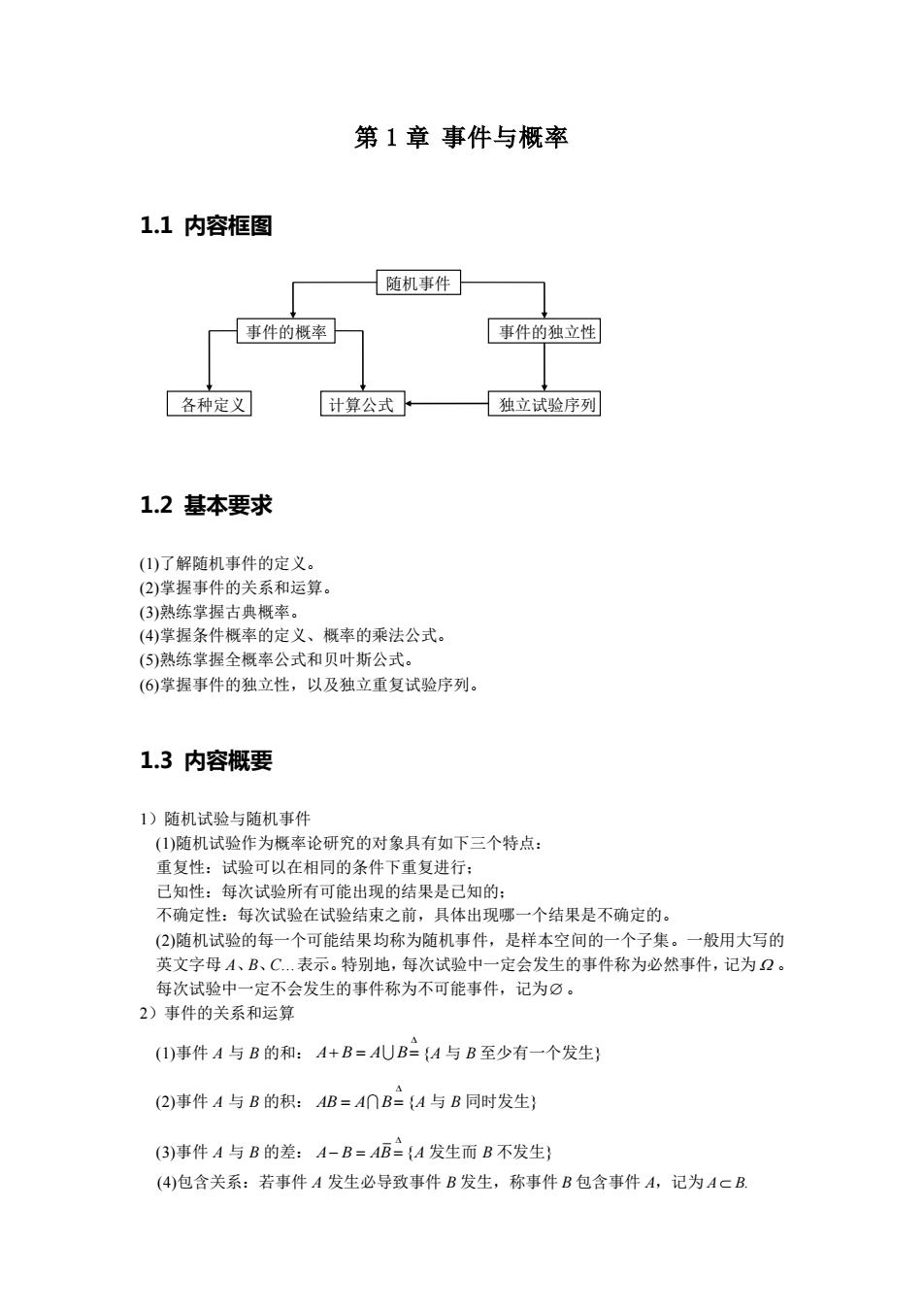
第1章事件与概率 1.1内容框图 随机事件 事件的概率 事件的独立性 各种定义 计算公式 独立试验序列 1.2基本要求 (1)了解随机事件的定义。 (2)掌握事件的关系和运算。 (3)熟练掌握古典概率。 (4)掌握条件概率的定义、概率的乘法公式。 (⑤)熟练掌握全概率公式和贝叶斯公式。 (6)掌握事件的独立性,以及独立重复试验序列。 1.3内容概要 1)随机试验与随机事件 (1)随机试验作为概率论研究的对象具有如下三个特点: 重复性:试验可以在相同的条件下重复进行: 己知性:每次试验所有可能出现的结果是己知的: 不确定性:每次试验在试验结束之前,具体出现哪一个结果是不确定的。 (2)随机试验的每一个可能结果均称为随机事件,是样本空间的一个子集。一般用大写的 英文字母A、B、C.表示。特别地,每次试验中一定会发生的事件称为必然事件,记为2。 每次试验中一定不会发生的事件称为不可能事件,记为⑦。 2)事件的关系和运算 (I)事件A与B的和:A+B=AUB={A与B至少有一个发生} (2)事件A与B的积:AB=A∩B={A与B同时发生} (3)事件A与B的差:A-B=AB={A发生而B不发生} (4)包含关系:若事件A发生必导致事件B发生,称事件B包含事件A,记为AcB
第 1 章 事件与概率 1.1 内容框图 随机事件 事件的概率 事件的独立性 各种定义 计算公式 独立试验序列 1.2 基本要求 (1)了解随机事件的定义。 (2)掌握事件的关系和运算。 (3)熟练掌握古典概率。 (4)掌握条件概率的定义、概率的乘法公式。 (5)熟练掌握全概率公式和贝叶斯公式。 (6)掌握事件的独立性,以及独立重复试验序列。 1.3 内容概要 1)随机试验与随机事件 (1)随机试验作为概率论研究的对象具有如下三个特点: 重复性:试验可以在相同的条件下重复进行; 已知性:每次试验所有可能出现的结果是已知的; 不确定性:每次试验在试验结束之前,具体出现哪一个结果是不确定的。 (2)随机试验的每一个可能结果均称为随机事件,是样本空间的一个子集。一般用大写的 英文字母 A、B、C…表示。特别地,每次试验中一定会发生的事件称为必然事件,记为 。 每次试验中一定不会发生的事件称为不可能事件,记为 。 2)事件的关系和运算 (1)事件 A 与 B 的和: A B A B + = = {A 与 B 至少有一个发生} (2)事件 A 与 B 的积: AB A B = = {A 与 B 同时发生} (3)事件 A 与 B 的差: A B AB − = = {A 发生而 B 不发生} (4)包含关系:若事件 A 发生必导致事件 B 发生,称事件 B 包含事件 A,记为 A B

(5)相等关系:若ACB且BCA,则称A与B相等,记为A=B. (⑥互不相容(互斥):若事件A与B不可能同时发生,即AB=⑦,则称A与B互不相容。 ()互相对立(互逆):若A与B同时满足:A+B=2,AB=O,则称A与B互相对立,B 为A的对立事件,记为B=A。 3)古典概率与几何概率 (1)古典概型具有两个特征: 有限性:样本点的个数为有限个: 等可能性:每个样本点发生的可能性相等。 在古典概型中,事件A的概率为 A包含的样本点数 P(A)= 样本点总数 (2)几何概型具有两个特征: ①试验的结果是无限且不可列的: ②每个结果发生的可能性是均匀的。 在几何概型中,事件A的概率为 P(A)=M. Mo 其中M与M。分别为事件A与样本空间2的几何度量。 4)概率的性质与运算公式 (1)0≤P(4)≤1,P(2)=1,P(O)=0。 (2)有限可加性:若A,A,…,An互不相容,则 (3)P(A)=1-P(4). (4)P(A-B)=P(AB)=P(A)-P(AB) 特别地,当BcA时,有P(A-B)=P(A)-P(B) (5)加法公式:对任意事件A、B、C,有 P(A+B)=P(A)+P(B)-P(AB) P(A+B+C)=P(A)+P(B)+P(C)-P(AB)-P(BC)-P(AC)+P(ABC) (6条件概率:当P(B)>0时,P(4B)=P4 P(B) (7)乘法公式:对任意两个事件A、B,当P(4)>0,P(B)>0时有 P(AB)=P(A)P(BIA)=P(B)P(AB) (⑧)全概率公式:设事件组B,B,,B,互不相容,且PB)>0,事件AcB,则有 P()=P(B)P(AIB) i= (9)贝叶斯公式:设事件组B,A,B,互不相容,且P(B)>0,事件AcB,则有
2 (5)相等关系:若 A B 且 B A ,则称 A 与 B 相等,记为 A B = . (6)互不相容(互斥):若事件 A 与 B 不可能同时发生,即 AB = ,则称 A 与 B 互不相容。 (7)互相对立(互逆):若 A 与 B 同时满足: A B AB + = = , ,则称 A 与 B 互相对立,B 为 A 的对立事件,记为 B A = 。 3)古典概率与几何概率 (1)古典概型具有两个特征: 有限性:样本点的个数为有限个; 等可能性:每个样本点发生的可能性相等。 在古典概型中,事件 A 的概率为 (2)几何概型具有两个特征: ①试验的结果是无限且不可列的; ②每个结果发生的可能性是均匀的。 在几何概型中,事件 A 的概率为 ( ) = MA P A M 其中 M M A与 分别为事件 A 与样本空间 的几何度量。 4)概率的性质与运算公式 (1) 0 ( ) 1, ( ) 1, ( ) 0 = = P A P P 。 (2)有限可加性:若 1 2 , , , A A A n 互不相容,则 1 1 ( ) = = = n n i i i i P A P A (3) P A P A ( ) 1 ( ) = − 。 (4) P A B P AB P A P AB ( ) ( ) ( ) ( ) − = = − 特别地,当 B A 时,有 P A B P A P B ( ) ( ) ( ) − = − (5)加法公式: 对任意事件 A、B、C,有 P A B P A P B P AB ( ) ( ) ( ) ( ) + = + − P A B C P A P B P C P AB P BC P AC P ABC ( ) ( ) ( ) ( ) ( ) ( ) ( ) ( ) + + = + + − − − + (6)条件概率:当 P B( ) 0 时, ( ) ( | ) ( ) = P AB P A B P B (7)乘法公式:对任意两个事件 A、B,当 P A P B ( ) 0, ( ) 0 时有 P AB P A P B A P B P A B ( ) ( ) ( | ) ( ) ( | ) = = (8)全概率公式:设事件组 1 2 , , , B B B n 互不相容,且 P B( ) 0 i ,事件 1 = = i n i i A B ,则有 1 ( ) ( ) ( | ) = = n i i i P A P B P A B (9)贝叶斯公式:设事件组 1 2 , , , B B B n 互不相容,且 P B( ) 0 i ,事件 1 = = i n i i A B ,则有 A包含的样本点数 样本点总数 P A( ) =

P(B)= P(B)P(AIB) (k=1,2,… P(B)P(AI B,) 5)事件的独立性 (I)定义:①对事件A与B,若P(AB)=P(A)P(B),则称A与B相互独立。 ②对n个事件A,4,…,An,如果其中任意m(2≤m≤m)个事件A,4,…,4都 有P4,A,,4)=P4)P4)…P4)则称4,4,,An相互独立。 (2)性质: ①当P(A)>0时,事件A与B相互独立一P(B)=P(B|A)。 特别地,必然事件2及不可能事件⑦与任一事件A都是相互独立的。 ②若事件A与B相互独立,则A与B,A与B,A与B也相互独立。 ③若事件A,4,,An相互独立,则其中任意m(2≤m≤)个事件仍相互独立。 6)独立试验序列(n重贝努利试验) (1)独立试验序列(n重贝努利试验)满足三个条件: ①每次试验只有两个结果:A与A: ②各次试验中,概率P(4)=pO<p<1)保持不变: ③各次试验的结果相互独立。 (2)性质:若在n重贝努利试验中,事件A发生的概率为p0<p<),则在n次试验中事 件A恰好发生k次的概率为 Pn(k)=Cp*q"-(其中k=0,1,2,…,mq=1-p) 1.4自测题一 一、判断题(对用“+”,错用“-”) 1.设A,B是两个事件,则事件A与B都不发生可表示成AB。 () 2.设A,B是两个事件,则事件A发生而事件B不发生可表示为A-AB。() 3.从编号为1到10的十张卡片中任取一张,若以A表示卡片编号是奇数,B表示卡片编号 小于5,则UB表示取到的卡片编号是6,8或10 () 4.设A,B是两个事件,若BcA,则AUB=⑦。 () 5.设A,B是两个事件,则A-BsA+B。 ( ) 6.设A,B是两个事件,则AB+BA=A+B-AB。 ) 7.如果事件A与B是对立事件,则A与B必互不相容。 ) 8.概率为零的事件必为不可能事件。 9.设A,B是任意两个事件,则必有P(A-B)=P(A)-P(B)。 ( 10.如果事件A与B互不相容,且P()>0,则P(B1A)=0。 11.如果事件A与B相互独立,则A与B必互不相容
3 1 ( ) ( | ) ( ) ( 1,2, ) ( ) ( | ) = = = k k k n i i i P B P A B P B k P B P A B 5)事件的独立性 (1)定义:①对事件 A 与 B,若 P AB P A P B ( ) ( ) ( ) = ,则称 A 与 B 相互独立。 ②对 n 个事件 1 2 , , , A A A n ,如果其中任意 m m n (2 ) 个事件 1 2 , , , i i im A A A 都 有 1 2 1 2 ( , , , ) ( ) ( ) ( ) = i i i i i i m m P A A A P A P A P A ,则称 1 2 , , , A A A n 相互独立。 (2)性质: ①当 P A( ) 0 时,事件 A 与 B 相互独立 = P B P B A ( ) ( | ) 。 特别地,必然事件 及不可能事件 与任一事件 A 都是相互独立的。 ②若事件 A 与 B 相互独立,则 A 与 B , A 与 B , A 与 B 也相互独立。 ③若事件 1 2 , , , A A A n 相互独立,则其中任意 m m n (2 ) 个事件仍相互独立。 6)独立试验序列(n 重贝努利试验) (1)独立试验序列(n 重贝努利试验)满足三个条件: ①每次试验只有两个结果:A 与 A ; ②各次试验中,概率 P A p p ( ) (0 1) = 保持不变; ③各次试验的结果相互独立。 (2)性质:若在 n 重贝努利试验中,事件 A 发生的概率为 p p (0 1) ,则在 n 次试验中事 件 A 恰好发生 k 次的概率为 ( ) ( 0,1,2, , ; 1 ) − = = = − k k n k P k C p q k n q p n n 其中 1.4 自测题一 一、判断题(对用“+”,错用“ − ”) 1.设 A,B 是两个事件,则事件 A 与 B 都不发生可表示成 AB 。 ( ) 2.设 A,B 是两个事件,则事件 A 发生而事件 B 不发生可表示为 A AB − 。( ) 3.从编号为 1 到 10 的十张卡片中任取一张,若以 A 表示卡片编号是奇数,B 表示卡片编号 小于 5,则 A B 表示取到的卡片编号是 6,8 或 10. ( ) 4.设 A,B 是两个事件,若 B A ,则 A B = 。 ( ) 5.设 A,B 是两个事件,则 A B A B − + 。 ( ) 6.设 A,B 是两个事件,则 AB BA A B AB + = + − 。 ( ) 7. 如果事件 A 与 B 是对立事件,则 A 与 B 必互不相容。 ( ) 8.概率为零的事件必为不可能事件。 9. 设 A,B 是任意两个事件,则必有 P A B P A P B ( ) ( ) ( ) − = − 。 ( ) 10. 如果事件 A 与 B 互不相容,且 P A( ) 0 ,则 P B A ( | ) 0 = 。 ( ) 11. 如果事件 A 与 B 相互独立,则 A 与 B 必互不相容。 ( )

12.如果事件A与B互不相容,则A与B也互不相容。 13.如果事件A与B相互独立,则A与B也相互独立。 14.袋中有大小相同的2个白球和4个黑球,现随机地将球从袋中逐一摸出,则第1次摸出 白球的概率必大于第3次摸出白球的概率。 () 15.两个箱子,第一个箱子中有4个黑球,2个白球,第二个箱子中有3个黑球,3个白球。 现随机取一个箱子,再从这个箱子中取一个球,若己知取出的是白球,则此球是从第二个箱 子中取出的可能性大。 () 二、填空题: 1.从10位同学中随机抽取3人担任不同职务,问共有种取法,从10位同 学中随机派3人参加会议,共有种取法。 2.某射手向目标射击3次,记4=“第i次命中目标”(i=1,2,3),则“前两次至少有 一次未命中目标”可表示为 3.概率的统计定义为 古典概率公式P(A)= 4.袋中有4个黑球,3个白球,大小、形状相同:一次随机摸出4个球,其中恰有3个白 球的概率为。 5.从一副52张的扑克牌中,随机地抽取5张,则其中至少有一张A的概率为_ 6.设A,B都是随机事件,若BcA,且P(A)=0.8,P(B)=04,则P(B|A)= 7.将P(A),P(A+B),P(AB),P(A)+P(B)按从小到大排列成为 8.已知P(A)=0.5,P(B=0.6,P(B|A)=0.8则P(4什B)= 9.设A、B为随机事件,P()=0.7,P(A-B)=0.3,则P(A+B)=。 10.已知P(A)=0.4,P(A+B)=0.7,那么,当A、B互不相容时,P(B)=;当A、B 互相独立时,P(B)= 11.甲、乙两厂生产的电池放在一起,己知其中有75%是甲厂生产,有25%是乙厂 生产的。甲厂电池的次品率为0.02,乙厂电池的次品率为0.04。现从中任意取出 的一个电池,则它是次品的概率为 12.设盒子中有10个木质球,6个玻璃球,玻璃球有2个为红色,4个为蓝色:木 质球有3个为红色,7个为蓝色。现从盒中任取一球,用A表示“取到蓝色球”, B表示“取到玻璃球”,则P(B|A)= 13.独立掷10枚均匀硬币,恰好出现一次正面的概率为 14.甲、乙两人独立地对同一目标各射击一次,其命中率分别为0.7和0.5。现己 知目标被命中,则它是乙射中的概率为
4 12. 如果事件 A 与 B 互不相容,则 A 与 B 也互不相容。 ( ) 13. 如果事件 A 与 B 相互独立,则 A 与 B 也相互独立。 ( ) 14. 袋中有大小相同的 2 个白球和 4 个黑球,现随机地将球从袋中逐一摸出,则第 1 次摸出 白球的概率必大于第 3 次摸出白球的概率。 ( ) 15.两个箱子,第一个箱子中有 4 个黑球,2 个白球,第二个箱子中有 3 个黑球,3 个白球。 现随机取一个箱子,再从这个箱子中取一个球,若已知取出的是白球,则此球是从第二个箱 子中取出的可能性大。 ( ) 二、填空题: 1.从 10 位同学中随机抽取 3 人担任不同职务,问共有______种取法,从 10 位同 学中随机派 3 人 参加会议,共有______种取法。 2. 某射手向目标射击3次,记 Ai =“第 i 次命中目标”( i = 1,2,3),则“前两次至少有 一次未命中目标”可表示为_________。 3. 概率的统计定义为_________________, 古典概率公式 P(A)= ____________。 4. 袋中有 4 个黑球,3 个白球,大小、形状相同;一次随机摸出 4 个球,其中恰有 3 个白 球的概率为______。 5.从一副 52 张的扑克牌中,随机地抽取 5 张,则其中至少有一张 A 的概率为___. 6. 设 A,B 都是随机事件,若 B A ,且 P A( ) 0.8 = , P B( ) 0.4 = ,则 P B A ( | ) = ________。 7. 将 P A P A B P AB P A P B ( ), ( ), ( ), ( ) ( ) + + 按从小到大排列成为_________________. 8. 已知 P(A)=0.5, P(B)=0.6, P(B| A) =0.8 则 P(A+B) =________。 9.设 A、B 为随机事件, P A P A B ( ) 0.7, ( ) 0.3, = − = 则 P A B ( ) ___ + = 。 10. 已知 P(A)=0.4, P(A+B)=0.7, 那么, 当 A、B 互不相容时,P(B)= ____;当 A、B 互相独立时,P(B)= _______。 11.甲、乙两厂生产的电池放在一起,已知其中有 75%是甲厂生产,有 25%是乙厂 生产的。甲厂电池的次品率为 0.02,乙厂电池的次品率为 0.04。现从中任意取出 的一个电池,则它是次品的概率为_______。 12.设盒子中有 10 个木质球,6 个玻璃球,玻璃球有 2 个为红色,4 个为蓝色;木 质球有 3 个为红色,7 个为蓝色。现从盒中任取一球,用 A 表示“取到蓝色球”, B 表示“取到玻璃球”,则 P B A ( | ) = ________。 13. 独立掷 10 枚均匀硬币,恰好出现一次正面的概率为______。 14.甲、乙两人独立地对同一目标各射击一次,其命中率分别为 0.7 和 0.5。现已 知目标被命中,则它是乙射中的概率为________

15.如图线路中元件A、B、C能正常工作的概率均为)且各元件独立工作,则 线路能正常工作的概率为 三、选择题: 1.在含有正品和次品的甲,乙产品中各抽取一件产品检验,记事件A={抽到甲产品是正品 且乙产品是次品},则事件A的对立事件A表示()。 (A){抽到甲产品是次品且乙产品是正品}:(B){抽到甲,乙产品都是次品}: (C){抽到甲产品是次品或乙产品是正品};(D){抽到甲,乙产品都是正品} 2.打靶3发,事件4表示“击中i发”(1=01,2,3),则事件A+4,+4表示()。 (A)全部击中:(B)至少击中一发:(C)击中3发:(D)至多击中3发 3.对任意二事件A,B,与A+B=B不等价的是()。 (A)ACB; (B)BCA; (C)AB=(D)AB= 4.将6本不同的外文书,4本不同的中文书,任意放入书架,则4本中文书放在一起的概 率为()。 (A) 4171 101 (B)7: 10 (C) 4161 (D) 101 10 5.向单位圆x2+y2<1内随机地投下3点,则这3点恰有2点落在第一象限内的概率为()。 w6 (B)3 64 (c)9 (D) 64 4 6.n张奖券中有m张是有奖的,现有k个人购买,每人一张,其中至少有一个人中奖的概 率为()。 容;m总01会;0器 Ck 7.设A、B是两个事件,则下列等式中()是不正确的。 (A)当A与B独立时,P(AB)=P(A)P(B): (B)当A与B互斥时,P(AB)=P(A)P(B)方 (C)当A与B互斥时,P(AB)=0; (D)P(AB)=P(A)P(BA). 8.设P(4)=0.8,P(B)=0.7,P(AB)=0.8,则下列结论正确的是()。 (A)事件A与B互不相容: (B)ACB: (C)事件A与B互相独立: (D)P(A+B)=P(A)+P(B). 9.每次试验成功的概率为p0<p<),则在3次独立重复试验中至少失败一次的概率为 ()。 (A)1-p)3;(B)1-p3;(C)31-p);(D)1-(1-p)3
5 15.如图线路中元件 A、B、C 能正常工作的概率均为 1 2 ,且各元件独立工作,则 线路能正常工作的概率为___________. 三、选择题: 1. 在含有正品和次品的甲,乙产品中各抽取一件产品检验,记事件 A ={抽到甲产品是正品 且乙产品是次品},则事件 A 的对立事件 A 表示( )。 (A) {抽到甲产品是次品且乙产品是正品}; (B){抽到甲,乙产品都是次品}; (C) {抽到甲产品是次品或乙产品是正品}; (D){抽到甲,乙产品都是正品}. 2.打靶 3 发,事件 Ai 表示“击中 i 发”( i = 0,1,2,3 ),则事件 A A A 1 2 3 + + 表示( )。 (A)全部击中;(B)至少击中一发;(C)击中 3 发;(D)至多击中 3 发. 3.对任意二事件 AB, ,与 A B B + = 不等价的是( )。 (A) ; (B) ; (C) ; (D) . A B B A AB AB = = 4.将 6 本不同的外文书,4 本不同的中文书,任意放入书架,则 4 本中文书放在一起的概 率为( )。 (A) 4!7! 10! ; (B) 7 10 ; (C) 4!6! 10! ; (D) 4 10 . 5. 向单位圆 2 2 x y + 1 内随机地投下3点,则这3点恰有2点落在第一象限内的概率为( )。 (A) 16 1 ; (B) 64 3 ; (C) 64 9 ; (D) 4 1 . 6. n 张奖券中有 m 张是有奖的,现有 k 个人购买,每人一张,其中至少有一个人中奖的概 率为( )。 (A) 1 1 k m n m k n C C C − − ; (B) k n m C ; (C) 1 k n m k n C C − − ; (D) 1 k r m k r n C = C . 7. 设 A、B 是两个事件,则下列等式中( )是不正确的。 (A) 当 A 与 B 独立时 ,P(AB)=P(A)P(B); (B) 当 A 与 B 互斥时,P(AB)=P(A)P(B); (C) 当 A 与 B 互斥时,P(AB) =0; (D) P(AB)=P(A)P(B|A). 8. 设 P A P B P A B ( ) 0.8, ( ) 0.7, ( | ) 0.8 = = = ,则下列结论正确的是( )。 (A)事件 A 与 B 互不相容; (B) A B ; (C)事件 A 与 B 互相独立; (D) P A B P A P B ( ) ( ) ( ) + = + . 9.每次试验成功的概率为 p p (0 1) ,则在 3 次独立重复试验中至少失败一次的概率为 ( )。 (A) 3 (1 ) − p ; (B) 3 1− p ; (C) 3(1 ) − p ; (D) 3 1 (1 ) − − p . A B C