第6章数理统计的基本概念 6.1内容框图 总体与样本 统计量 点估计 矩阵估计 点估计的评价 极大似然估计 常用统计量定义 统计量的分布 三大抽样分布 正态总体统计量的分布 6.2基本要求 (1)理解总体、样本及统计量的概念,并熟练掌握常用统计量的公式 (2)掌握矩法估计和极大似然估计的求法,以及估计无偏性、有效性的判断 (3)掌握三大抽样分布定义,并记住其概率密度的形状 (4)理解并掌握有关正态总体统计量分布的几个结论,如定理6.4~6.9及定理6.11 6.3内容概要 1)总体与样本 在数理统计中,我们把作为统计研究对象的随机变量称为总体,记为,门,…。对 总体进行n次试验后所得到的结果,称为样本,记为(X1,X2,…,Xn), (Y,Y2,…,Yn),…,其中,试验次数n称为样本容量。样本(X,X2,…,Xn)中的 每一个X,都是随机变量。样本所取的一组具体的数值,称为样本观测值,记为 93
93 第6章 数理统计的基本概念 6.1 内容框图 6.2 基本要求 (1) 理解总体、样本及统计量的概念,并熟练掌握常用统计量的公式. (2) 掌握矩法估计和极大似然估计的求法,以及估计无偏性、有效性的判断. (3) 掌握三大抽样分布定义,并记住其概率密度的形状. (4) 理解并掌握有关正态总体统计量分布的几个结论,如定理 6.4~6.9 及定理 6.11. 6.3 内容概要 1) 总体与样本 在数理统计中,我们把作为统计研究对象的随机变量称为总体,记为 , ,… 。对 总 体 进 行 n 次 试 验 后 所 得 到 的 结 果 , 称 为 样 本 , 记 为 ( X X Xn , , , 1 2 ), ( Y Y Yn , , , 1 2 ),……,其中,试验次数 n 称为样本容量。样本( X X Xn , , , 1 2 )中的 每一个 X i 都是随机变量。样本所取的一组具体的数值,称为样本观测值,记为 总体与样本 统计量 点估计 矩阵估计 常用统计量定义 布 统计量的分布 正态总体统计量的分布 点估计的评价 极大似然估计 三大抽样分布

(X1,X2,…,Xn)。 具有性质: (1)独立性,即X1,X2,…,X,相互独立。 (2)同分布性,即每一个X,都与总体5服从相同的分布。 称为简单随机样本。 如果总体5是离散型随机变量,概率分布为P{5=k},那么样本(X1,X2,…,Xn) 的联合概率分布为PX=,X:=,X。=x}=广PX,=}=1P传=x: 如果总体5是连续型随机变量,概率密度为p(x),那么样本(X1,X2,…,Xn)的 联合概率密度为*(3,x2,,x,)=门xG,)=·(x)。 如果总体5的分布函数为F(x),那么样本(X,X2,…,Xn)的联合分布函数为 F*(a,)=Fxc,)=IF)· 2)用样本估计总体的分布 数理统计的一个主要任务,就是要用样本估计总体的分布。 参数估计又可以分为两种,一种是点估计,另一种是区间估计。 3)矩法估计 求矩法估计的步骤为: (1)计算总体分布的矩E(5)=f(0,02,…,0m),k=1,2,…,m,计算到m阶矩 为止(m是总体分布中未知参数的个数)。 (2)列方程 f(⑧,2,…,6n)=Eξ-元 f(6,62,…,6n)=E(52)=X2 fn(d,82,…,6n)=E5m)=Xm 从方程中解出日1,02,…,0,m,它们就是未知参数日1,02,…,0m的矩法估计。 g
94 ( n x , x , , x 1 2 ) 。 具有性质: (1)独立性,即 X X Xn , , , 1 2 相互独立。 (2)同分布性,即每一个 X i 都与总体 服从相同的分布。 称为简单随机样本 。 如果总体 是离散型随机变量,概率分布为 P{ = k} ,那么样本( X X Xn , , , 1 2 ) 的联合概率分布为 = = = = = = = = = n i i n i n n i i P X x X x X x P X x P x 1 1 1 1 2 2 { , ,, } { } { }。 如果总体 是连续型随机变量,概率密度为 (x) ,那么样本( X X Xn , , , 1 2 )的 联合概率密度为 = = = = n i i n i n X i x x x x x i 1 1 1 2 *( , ,, ) ( ) ( ) 。 如果总体 的分布函数为 F(x) ,那么样本( X X Xn , , , 1 2 )的联合分布函数为 = = = = n i i n i n X i F x x x F x F x i 1 1 1 2 *( , ,, ) ( ) ( ) 。 2)用样本估计总体的分布 数理统计的一个主要任务,就是要用样本估计总体的分布。 参数估计又可以分为两种,一种是点估计,另一种是区间估计。 3) 矩法估计 求矩法估计的步骤为: (1)计算总体分布的矩 ( ) ( , , , ) k 1 2 m k E = f ,k = 1,2, ,m ,计算到 m 阶矩 为止( m 是总体分布中未知参数的个数)。 (2)列方程 = = = = = = m m m m m m f E X f E X f E X ) ( ) ˆ , , ˆ , ˆ ( ) ( ) ˆ , , ˆ , ˆ ( ) ˆ , , ˆ , ˆ ( 1 2 2 2 2 1 2 1 1 2 从方程中解出 m ˆ , , ˆ , ˆ 1 2 ,它们就是未知参数 m , , , 1 2 的矩法估计

4)极大似然估计 求极大似然估计的步骤为: (1)写出似然函数L的表达式。 如果总体5是离散型随机变量,概率分布为P5=k:,那么L=门P5=}: 如果总体5是连续型随机变量,概率密度为(x),那么L= Io(x). (2)在日,92,…,日的取值范围⊙内,求出使得似然函数L达到最大的参数估计值 日,,…,日。,它们就是未知参数的极大似然估计。 通常的做法是,先取对数nL(因为当nL达到最大时,L也达到最大)。 然后令hL关于0,02,…,日m的偏导数等于0,得到方程组 ain L=0 a0 。年果果。3 am L=0 a0 由此可见,如果上面这个方程组在日内有唯一解日,日2,…,日m,所以,按照极大 似然估计的定义,6,02,…,0就是未知参数日,02,…,0n的极大似然估计。 5) 衡量点估计好坏的标准 定理 设总体5的数学期望E5和方差D5都存在,(X1,X2,,Xn)是5的 样本,X是样本均值,S2是样本方差,则有 (1)EX=E5; 2)Dr=D5,(3)ES)="-lD5. n n 衡量点估计的好坏标准: (1)无偏性 定义6.1设0是参数0的估计,如果有E0=0,则称0是0的无偏估计。 (2)有效性 定义6.2设8,,日,都是参数0的无偏估计,如果有D(0)≤D(02),则称日,比 5
95 4) 极大似然估计 求极大似然估计的步骤为: (1)写出似然函数 L 的表达式。 如果总体 是离散型随机变量,概率分布为 P{ = k} ,那么 = = = n i i L P x 1 { } ; 如果总体 是连续型随机变量,概率密度为 (x) ,那么 = = n i i L x 1 ( ) 。 (2)在 m , , , 1 2 的取值范围 内,求出使得似然函数 L 达到最大的参数估计值 m ˆ , , ˆ , ˆ 1 2 ,它们就是未知参数的极大似然估计。 通常的做法是,先取对数 ln L (因为当 ln L 达到最大时, L 也达到最大)。 然后令 ln L 关于 m , , , 1 2 的偏导数等于 0,得到方程组 = = 0 ln 0 ln 1 m L L 由此可见,如果上面这个方程组在 内有唯一解 m ˆ , , ˆ , ˆ 1 2 ,所以,按照极大 似然估计的定义, m ˆ , , ˆ , ˆ 1 2 就是未知参数 m , , , 1 2 的极大似然估计。 5) 衡量点估计好坏的标准 定理 设总体 的数学期望 E 和方差 D 都存在,( X X Xn , ,..., 1 2 )是 的 样本, X 是样本均值, 2 S 是样本方差,则有 (1) EX = E ; (2) n D DX = ; (3) D n n E S 1 ( ) 2 − = 。 衡量点估计的好坏标准: (1) 无偏性 定义 6.1 设 ˆ 是参数 的估计,如果有 = E ˆ ,则称 ˆ 是 的无偏估计。 (2) 有效性 定义 6.2 设 1 ˆ , 2 ˆ 都是参数 的无偏估计,如果有 ) ˆ ) ( ˆ ( D 1 D 2 ,则称 1 ˆ 比

62有效。 (3)相合性(一致性) 定义6.3设0是参数0的估计,n是样本容量,如果任何6>0,都有 mP6-0<e}=1, 则称0是0的相合估计(一致估计)。 可以证明,矩法估计都是相合估计。除了极个别的例外,极大似然估计也都是相合估计。 6)数理统计中几个常用的分布 X2分布 定义6.4若有X1,X2,,Xn相互独立,X,~N(0,1),i=1,2,…,n,则称 X: 所服从的分布为自由度是n的x2分布,记为x(n)。 x2分布的概率密度为 e x>0 p(x)= 2r9 0 x≤0 X2分布的图象见图6-2。 y p(x) 0 x=2-2 图6-2 定理如果有5~X2(m),n~x2(nm),相互独立,则5+7~x2(m+n)。即x2 分布具有可加性。 96
96 2 ˆ 有效。 (3)相合性(一致性) 定义 6.3 设 ˆ 是参数 的估计, n 是样本容量,如果任何 0 ,都有 } 1 ˆ lim { − = → P n , 则称 ˆ 是 的相合估计(一致估计)。 可以证明,矩法估计都是相合估计。除了极个别的例外,极大似然估计也都是相合估计。 6) 数理统计中几个常用的分布 2 分布 定义 6.4 若有 X X Xn , ,..., 1 2 相互独立, X i ~ N(0, 1),i = 1, 2, , n ,则称 = n i Xi 1 2 所服从的分布为自由度是 n 的 2 分布,记为 ( ) 2 n 。 2 分布的概率密度为 = − − 0 0 0 ) 2 2 ( 1 ( ) 2 1 2 2 x x e x n x n x n 2 分布的图象见图 6-2 。 定理 如果有 ~ ( ) 2 m , ~ ( ) 2 n ,相互独立,则 + ~ ( ) 2 m + n 。即 2 分布具有可加性。 图 6-2 2 布的概率密度
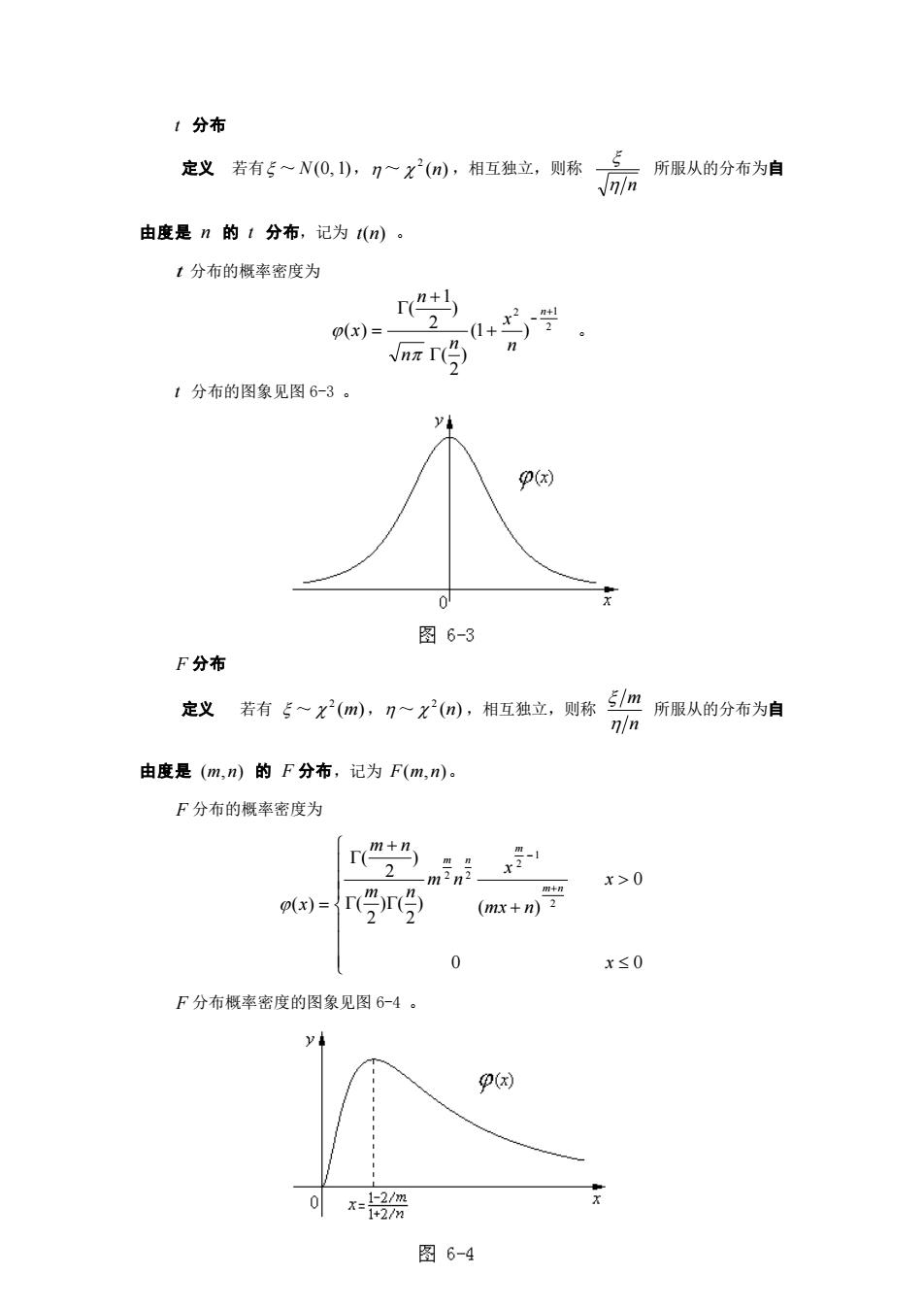
1分布 定义若有5~N(0,1),7~x2(n),相互独立,则称 5 所服从的分布为自 n/n 由度是n的t分布,记为t(n)。 1分布的概率密度为 p(x)= 2 n 1分布的图象见图6-3。 y p(x) 0 图6-3 F分布 定义若有5~x(m),7~x2(n),相互独立,则称 5/m 所服从的分布为自 n/n 由度是(m,n)的F分布,记为F(m,n)。 F分布的概率密度为 m+n 2 m n r学r m2n2 x>0 p(x)= 2 r+列 0 x≤0 F分布概率密度的图象见图6-4。 P) 0 x=12m 1+2/2 图6-4
97 t 分布 定义 若有 ~ N(0, 1), ~ ( ) 2 n ,相互独立,则称 n 所服从的分布为自 由度是 n 的 t 分布,记为 t(n) 。 t 分布的概率密度为 2 2 1 (1 ) ) 2 ( ) 2 1 ( ( ) + − + + = n n x n n n x 。 t 分布的图象见图 6-3 。 F 分布 定义 若有 ~ ( ) 2 m , ~ ( ) 2 n ,相互独立,则称 n m 所服从的分布为自 由度是 (m, n) 的 F 分布,记为 F(m, n)。 F 分布的概率密度为 + + = + − 0 0 0 ( ) ) 2 ) ( 2 ( ) 2 ( ( ) 2 1 2 2 2 x x mx n x m n m n m n x m n m m n F 分布概率密度的图象见图 6-4