
《抽象代数》教学大纲 一、课程基本信息 课程编码:061112B 中文名称:抽象代数 英文名称:Abstract Algebra 课程类别:专业基础课程 总学时:48(理论40,实践8) 总学分:3 适用专业:数学与应用数学 先修课程:高等代数 二、课程的性质、目标和任务 抽象代数(或近世代数)是数学与应用数学专业学生的一门专业课,是高等代数的继续和提 高,本课程主要研究各种代数系统-一群、环、域等的结构。通过本课程的学习,使学生获得一定的 抽象代数基础知识,受到代数方法的初步训练,提高辩证思维和逻辑推理能力,并为进一步学习专 业知识打下基础。 三、课程教学基本要求 1、授课:以课堂讲授为主,采取板书配以多媒体的方式。 2、习题课:进行典型问题分析,方法总结,难题讲解,与学生黑板演题相结合,训练学生的 逻辑思维能力,解题能力和思维严密性。 3、作业:每次课后配以一定量的书面作业,按学院统一要求每周批改一次。 4、辅导:每周进行答疑辅导。 四、课程教学内容及要求 第一章基本概念(6学时) 【教学目标与要求】 1、理解代数运算,同态与同构等概念。 2、掌握等价关系,集合的分类等概念。 【教学重点与难点】 -1-
-1- 《抽象代数》教学大纲 一、课程基本信息 课程编码:061112B 中文名称:抽象代数 英文名称:Abstract Algebra 课程类别:专业基础课程 总 学 时:48(理论 40,实践 8) 总 学 分:3 适用专业:数学与应用数学 先修课程:高等代数 二、课程的性质、目标和任务 抽象代数(或近世代数)是数学与应用数学专业学生的一门专业课,是高等代数的继续和提 高,本课程主要研究各种代数系统---群、环、域等的结构。通过本课程的学习,使学生获得一定的 抽象代数基础知识,受到代数方法的初步训练,提高辩证思维和逻辑推理能力,并为进一步学习专 业知识打下基础。 三、课程教学基本要求 1、授课:以课堂讲授为主,采取板书配以多媒体的方式。 2、习题课:进行典型问题分析,方法总结,难题讲解,与学生黑板演题相结合,训练学生的 逻辑思维能力,解题能力和思维严密性。 3、作业:每次课后配以一定量的书面作业,按学院统一要求每周批改一次。 4、辅导:每周进行答疑辅导。 四、课程教学内容及要求 第一章 基本概念(6 学时) 【教学目标与要求】 1、理解代数运算,同态与同构等概念。 2、掌握等价关系,集合的分类等概念。 【教学重点与难点】

1、教学重点:代数运算、同态与同构。 2、教学难点:等价关系与集合分类的内在联系。 【教学内容】 1.1集合 1.2映射与变换 1.3代数运算 1.4运算律 1.5同态与同构 1.6等价关系与集合的分类 第二章群(16学时) 【教学目标与要求】 1、掌握群和半群的定义,熟知群和半群的一些典型实例:理解元素阶的定义和性质。 2、理解并掌握循环群的概念和表示。 3、了解变换群,理解置换群。 4、理解陪集、指数的概念和lagrange定理。 【教学重点与难点】 1、教学重点:群的概念,子群、循环群、置换群、陪集的概念和基本性质。 2、教学难点:变换群。 【教学内容】 2.1群的定义和初步性质 2.2群中元素的阶 2.3子群 2.4循环群 2.5变换群 2.6置换群 2.7陪集、指数和Lagrange定理 第三章正规子群和群的同态与同构(14学时) -2一
-2- 1、教学重点:代数运算、同态与同构。 2、教学难点:等价关系与集合分类的内在联系。 【教学内容】 1.1 集合 1.2 映射与变换 1.3 代数运算 1.4 运算律 1.5 同态与同构 1.6 等价关系与集合的分类 第二章 群(16 学时) 【教学目标与要求】 1、掌握群和半群的定义,熟知群和半群的一些典型实例;理解元素阶的定义和性质。 2、理解并掌握循环群的概念和表示。 3、了解变换群,理解置换群。 4、理解陪集、指数的概念和 lagrange 定理。 【教学重点与难点】 1、教学重点:群的概念,子群、循环群、置换群、陪集的概念和基本性质。 2、教学难点:变换群。 【教学内容】 2.1 群的定义和初步性质 2.2 群中元素的阶 2.3 子群 2.4 循环群 2.5 变换群 2.6 置换群 2.7 陪集、指数和 Lagrange 定理 第三章 正规子群和群的同态与同构(14 学时)

【教学目标与要求】 1、掌握正规子群和商群的定义和性质。 2、掌握同态与同构映射下群的基本性质。 3、理解群的同态基本定理。 4、了解群的同构定理。 5、了解群的自同构群。 【教学重点与难点】 1、教学重点:正规子群、商群、群的同态基本定理。 2、教学难点:群的自同构群。 【教学内容】 3.1群同态与同构的简单性质 3.2正规子群和商群 3.3群同态基本定理 3.4群的同构定理 3.5群的自同构群 第四章环与域(12学时) 【教学目标与要求】 1、掌握环的定义与一些例子。 2、掌握整环、除环和域的概念。 3、掌握理想、商环和环的同态等概念和性质。 4、掌握模n剩余类环。 5、了解多项式环。 6、了解素理想,极大理想,主理想。 【教学重点与难点】 1、教学重点:环的定义、理想、模n剩余类环。 2、教学难点:环的构造。 【教学内容】 -3一
-3- 【教学目标与要求】 1、掌握正规子群和商群的定义和性质。 2、掌握同态与同构映射下群的基本性质。 3、理解群的同态基本定理。 4、了解群的同构定理。 5、了解群的自同构群。 【教学重点与难点】 1、教学重点:正规子群、商群、群的同态基本定理。 2、教学难点:群的自同构群。 【教学内容】 3.1 群同态与同构的简单性质 3.2 正规子群和商群 3.3 群同态基本定理 3.4 群的同构定理 3.5 群的自同构群 第四章 环与域(12 学时) 【教学目标与要求】 1、掌握环的定义与一些例子。 2、掌握整环、除环和域的概念。 3、掌握理想、商环和环的同态等概念和性质。 4、掌握模 n 剩余类环。 5、了解多项式环。 6、了解素理想,极大理想,主理想。 【教学重点与难点】 1、教学重点:环的定义、理想、模 n 剩余类环。 2、教学难点:环的构造。 【教学内容】
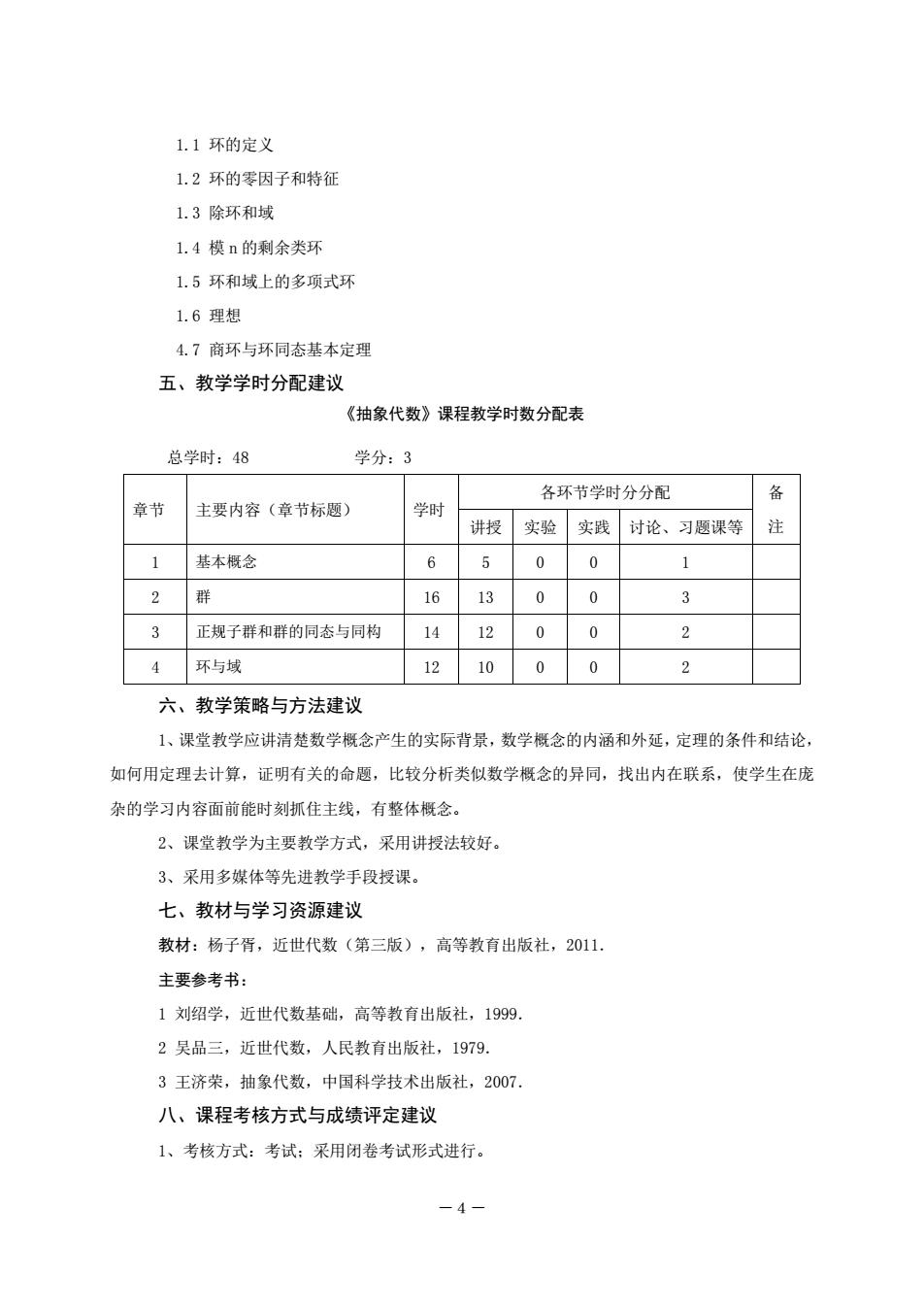
1.1环的定义 1.2环的零因子和特征 1.3除环和域 1.4模n的剩余类环 1.5环和域上的多项式环 1.6理想 4.7商环与环同态基本定理 五、教学学时分配建议 《抽象代数》课程教学时数分配表 总学时:48 学分:3 各环节学时分分配 备 章节 主要内容(章节标题) 学时 讲授 实验 实践 讨论、习题课等 注 1 基本概念 5 0 0 2 群 16 13 0 0 3 3 正规子群和群的同态与同构 14 12 0 0 2 4 环与域 12 10 0 0 2 六、教学策略与方法建议 1、课堂教学应讲清楚数学概念产生的实际背景,数学概念的内涵和外延,定理的条件和结论, 如何用定理去计算,证明有关的命题,比较分析类似数学概念的异同,找出内在联系,使学生在庞 杂的学习内容面前能时刻抓住主线,有整体概念。 2、课堂教学为主要教学方式,采用讲授法较好。 3、采用多媒体等先进教学手段授课。 七、教材与学习资源建议 教材:杨子胥,近世代数(第三版),高等教育出版社,2011. 主要参考书: 1刘绍学,近世代数基础,高等教育出版社,1999. 2吴品三,近世代数,人民教育出版社,1979 3王济荣,抽象代数,中国科学技术出版社,2007 八、课程考核方式与成绩评定建议 1、考核方式:考试:采用闭卷考试形式进行。 一4-
-4- 1.1 环的定义 1.2 环的零因子和特征 1.3 除环和域 1.4 模 n 的剩余类环 1.5 环和域上的多项式环 1.6 理想 4.7 商环与环同态基本定理 五、教学学时分配建议 《抽象代数》课程教学时数分配表 总学时:48 学分:3 章节 主要内容(章节标题) 学时 各环节学时分分配 备 讲授 实验 实践 讨论、习题课等 注 1 基本概念 6 5 0 0 1 2 群 16 13 0 0 3 3 正规子群和群的同态与同构 14 12 0 0 2 4 环与域 12 10 0 0 2 六、教学策略与方法建议 1、课堂教学应讲清楚数学概念产生的实际背景,数学概念的内涵和外延,定理的条件和结论, 如何用定理去计算,证明有关的命题,比较分析类似数学概念的异同,找出内在联系,使学生在庞 杂的学习内容面前能时刻抓住主线,有整体概念。 2、课堂教学为主要教学方式,采用讲授法较好。 3、采用多媒体等先进教学手段授课。 七、教材与学习资源建议 教材:杨子胥,近世代数(第三版),高等教育出版社,2011. 主要参考书: 1 刘绍学,近世代数基础,高等教育出版社,1999. 2 吴品三,近世代数,人民教育出版社,1979. 3 王济荣,抽象代数,中国科学技术出版社,2007. 八、课程考核方式与成绩评定建议 1、考核方式:考试;采用闭卷考试形式进行

2、考核可以采用结构成绩,如平时占50%,期末占50%。 九、其他需要说明的问题 根据2017年修订的《数学与应用数学专业培养方案》的要求,以及运城学院教学型、地方性 和应用型的特色,并参考了其它国内同类高校相同专业该课程的大纲,制定了此教学大纲。 制订:数学与信息技术学院 教研室:数学与应用数学教研室 执笔人:刘汉武 审订人:王琦 -5-
-5- 2、考核可以采用结构成绩,如平时占 50%,期末占 50%。 九、其他需要说明的问题 根据 2017 年修订的《数学与应用数学专业培养方案》的要求,以及运城学院教学型、地方性 和应用型的特色,并参考了其它国内同类高校相同专业该课程的大纲,制定了此教学大纲。 制 订:数学与信息技术学院 教研室:数学与应用数学教研室 执笔人:刘汉武 审订人:王琦