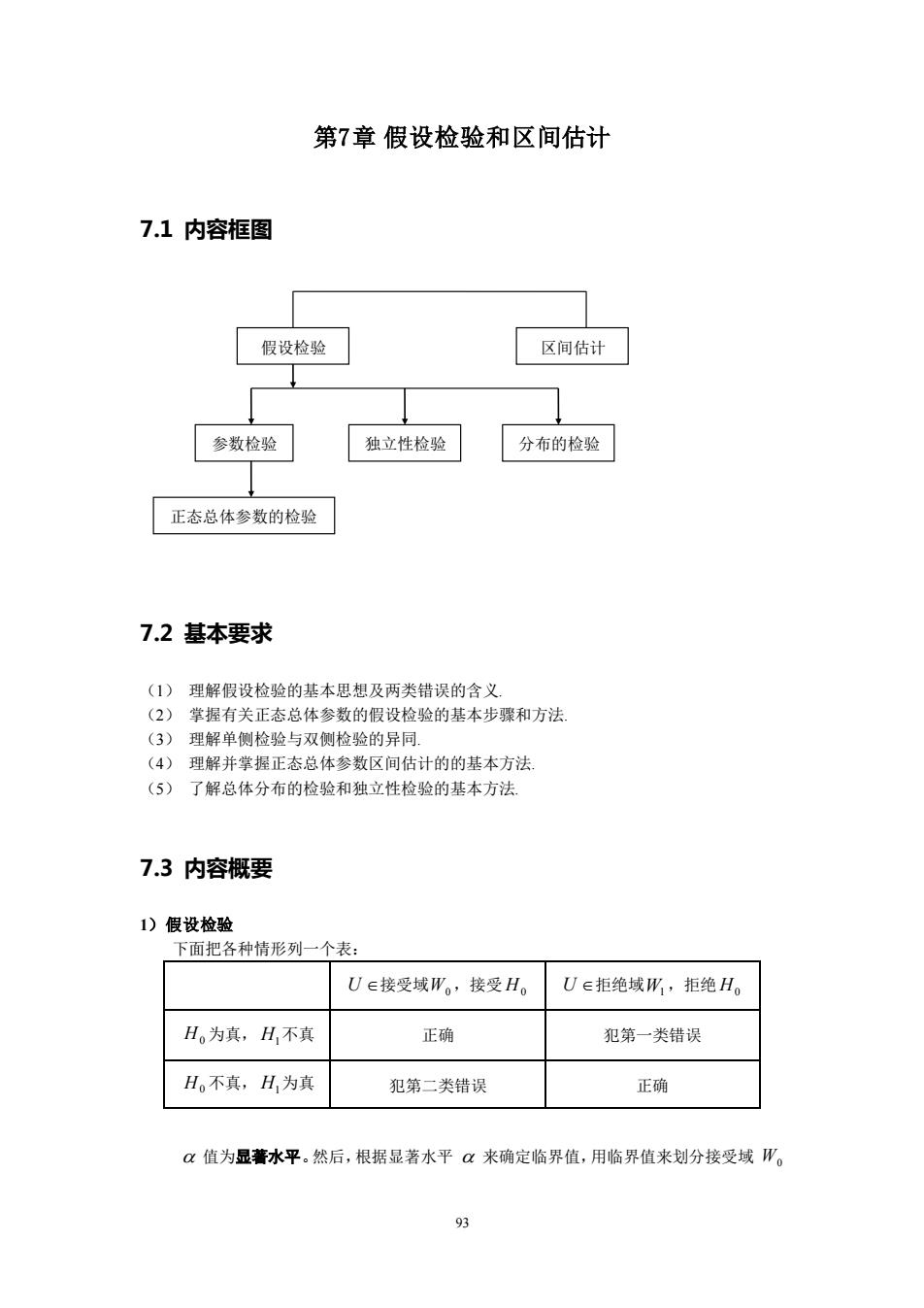
第7章假设检验和区间估计 7.1内容框图 假设检验 区间估计 参数检验 独立性检验 分布的检验 正态总体参数的检验 7.2基本要求 (1) 理解假设检验的基本思想及两类错误的含义 (2)掌握有关正态总体参数的假设检验的基本步骤和方法 (3)理解单侧检验与双侧检验的异同 (4)理解并掌握正态总体参数区间估计的的基本方法 (5)了解总体分布的检验和独立性检验的基本方法 7.3内容概要 1)假设检验 下面把各种情形列一个表: U∈接受域W。,接受H。 U∈拒绝域W,拒绝H。 H。为真,H不真 正确 犯第一类错误 Ho不真,H为真 犯第二类错误 正确 α值为显著水平。然后,根据显著水平α来确定临界值,用临界值来划分接受域W。 93
93 第7章 假设检验和区间估计 7.1 内容框图 7.2 基本要求 (1) 理解假设检验的基本思想及两类错误的含义. (2) 掌握有关正态总体参数的假设检验的基本步骤和方法. (3) 理解单侧检验与双侧检验的异同. (4) 理解并掌握正态总体参数区间估计的的基本方法. (5) 了解总体分布的检验和独立性检验的基本方法. 7.3 内容概要 1)假设检验 下面把各种情形列一个表: U 接受域 W0 ,接受 H0 U 拒绝域 W1 ,拒绝 H0 H0 为真, H1 不真 正确 犯第一类错误 H0 不真, H1 为真 犯第二类错误 正确 值为显著水平。然后,根据显著水平 来确定临界值,用临界值来划分接受域 W0 假设检验 区间估计 参数检验 分布的检验 正态总体参数的检验 独立性检验

和拒绝域W。这样的检验,称为显著性检验。 假设检验的一般步骤是: (1)提出原假设H。: (2)选取合适的检验统计量U,从样本求出U的值: (3)对于给定的显著水平《,查U的分布表,求出临界值,用它划分接受域W。 和拒绝域W,使得当H。为真时,有P{U∈W}=a: (4)若U的值落在拒绝域W,中,就拒绝H。,若U的值落在接受域W。中, 就接受H。。 假设检验的理论依据是所谓的小概率事件原理,即一个概率很小的事件在一次试验中几 乎是不可能发生的要检验一个根据实际问题提出的原假设H。是否成立,如果已知在H。成 立时,某个事件发生的可能性很小,而试验的结果却是这个事件发生了,那么根据小概率事 件原理,我们就可以认为所提出的这个假设H。是不成立的,即拒绝H。;反之,则接受H。 这里的原假设H。可以根据实际问题提出,事件是否发生可根据试验观测值判断,因此假设 检验的关键问题就是要确定在H。成立时,发生可能性很小的某个事件我们知道,正态分布 有个3σ原则,即三若服从正态分布,那么5的取值会大多集中在其均值附近,落入两侧的 可能性很小.事实上,当5服从t分布,x分布,F分布时,其取值落入两侧的可能性也都 相对很小.因此,我们要确定H。成立时一个发生可能性很小的事件,只需根据样本构造出服 从正态分布,t分布,x分布或F分布的随机变量(统计量)就可以了. 根据上述分析,正态总体参数的假设检验可概括为如下步骤。 (1)提出假设: 假设一般是根据实际问题提出的,只是为了检验的方便,要求原假设H。必须含有等号 (2)构造统计量: 即根据样本构造服从正态分布,t分布,x分布或F分布的不含未知参数的随机变量, 常用到6.7节的结论 例如,总体5~N4,o)其中σ已知,要检验Ho:=,己知的 U=X-n~N0,)
94 和拒绝域 W1 。这样的检验,称为显著性检验。 假设检验的一般步骤是: (1)提出原假设 H0 ; (2)选取合适的检验统计量 U ,从样本求出 U 的值; (3)对于给定的显著水平 ,查 U 的分布表,求出临界值,用它划分接受域 W0 和拒绝域 W1 ,使得当 H0 为真时,有 P{U W1 } = ; (4)若 U 的值落在拒绝域 W1 中,就拒绝 H0 ,若 U 的值落在接受域 W0 中, 就接受 H0 。 假设检验的理论依据是所谓的小概率事件原理,即一个概率很小的事件在一次试验中几 乎是不可能发生的.要检验一个根据实际问题提出的原假设 H0 是否成立,如果已知在 H0 成 立时,某个事件发生的可能性很小,而试验的结果却是这个事件发生了,那么根据小概率事 件原理,我们就可以认为所提出的这个假设 H0 是不成立的,即拒绝 H0 ;反之,则接受 H0 . 这里的原假设 H0 可以根据实际问题提出,事件是否发生可根据试验观测值判断,因此假设 检验的关键问题就是要确定在 H0 成立时,发生可能性很小的某个事件.我们知道,正态分布 有个 3 原则,即 若服从正态分布,那么 的取值会大多集中在其均值附近,落入两侧的 可能性很小.事实上,当 服从 t 分布, 2 x 分布,F 分布时,其取值落入两侧的可能性也都 相对很小.因此,我们要确定 H0 成立时一个发生可能性很小的事件,只需根据样本构造出服 从正态分布,t 分布, 2 x 分布或 F 分布的随机变量(统计量)就可以了. 根据上述分析,正态总体参数的假设检验可概括为如下步骤。 (1)提出假设: 假设一般是根据实际问题提出的,只是为了检验的方便,要求原假设 H0 必须含有等号. (2)构造统计量: 即根据样本构造服从正态分布,t 分布, 2 x 分布或 F 分布的不含未知参数的随机变量, 常用到 6.7 节的结论. 例如,总体 ( ) 2 0 ~ N , 其中 2 0 已知,要检验 H0 : = 0 ,已知的 ~ (0,1) 0 0 n N x U − =

T=x-n~n-), xs+f-Ar 00 都可用作检验的统计量但是T忽略了σ。己知的信息肯定不如U好,而x2因其概率密度的 复杂性(这使得H。的最小接受域难以确定),它也不如U统计量好.其他统计量如 x2=2 rh- 因不含4。显然无法用于检验 一般地,关于期望的检验用U统计量或T统计量.关于单个正态总体方差的检验用x2统计量 关于两个正态总体方差的检验用F统计量: (3)确定拒绝域: 拒绝域就是在H。为真的情况下,所构造的统计量以很小的概率(显著性水平ā)落入的范 围,记为W,即P{统计量∈W}=ā.根据原假设形式上的不同,拒绝域可能为单侧或双侧 那么如何确定拒绝域究竟在左侧,右侧还是双侧呢?比如我们用U=X一山√n来检验 00 H。:4=4时,在H成立的情况下,U的取值应集中在其中心原点附近,取值偏大或 偏小都是可能的,但可能性会很小.因此,此时H。的拒绝域为双侧的但是如果要检验的H。 为μ≥4,此时有U=二凸Vn≥-么n、N0,),即在H。成立时,U的取值会偏 00 大,故此时H。的拒绝域在左侧.一个简单的判别准则是:单侧检验中拒绝域的不等号方向与 备选假设的不等号方向一致,即H,:4<4,则拒绝域为U<一山a (4)作出判断: 代入样本观测值,若统计量观测值落入拒绝域W则拒绝原假设:否则接受原假设 上述步骤也同样适用于非参数检验,如关于分布的检验和独立性检验只不过分布的检验和 独立性检验都是以x2分布为检验统计量并且都是单侧检验. 的
95 ~ ( 1) * 0 − − = n t n S x T , ( ) x (n) ns n x x 2 2 0 2 0 2 2 ~ + − = 都可用作检验的统计量.但是 T 忽略了 2 0 已知的信息肯定不如 U 好,而 2 x 因其概率密度的 复杂性(这使得 H0 的最小接受域难以确定),它也不如 U 统计量好.其他统计量如 ~ ( 1) 2 2 0 2 2 = x n − nS x , 因不含 0 显然无法用于检验. 一般地,关于期望的检验用 U 统计量或 T 统计量.关于单个正态总体方差的检验用 2 x 统计量. 关于两个正态总体方差的检验用 F 统计量. (3) 确定拒绝域: 拒绝域就是在 H0 为真的情况下,所构造的统计量以很小的概率(显著性水平α)落入的范 围,记为 W1 ,即 P{统计量∈ W1 }=α.根据原假设形式上的不同,拒绝域可能为单侧或双侧. 那么如何确定拒绝域究竟在左侧,右侧还是双侧呢?比如我们用 n x U 0 0 − = 来检验 H0 : = 0 时,在 H0 成立的情况下, U 的取值应集中在其中心原点附近,取值偏大或 偏小都是可能的,但可能性会很小.因此,此时 H0 的拒绝域为双侧的.但是如果要检验的 H0 为 0 ,此时有 ~ (0,1) 0 0 0 0 n N x n x U − − = ,即在 H0 成立时, U 的取值会偏 大,故此时 H0 的拒绝域在左侧.一个简单的判别准则是:单侧检验中拒绝域的不等号方向与 备选假设的不等号方向一致,即 1 0 H : ,则拒绝域为 U −u1−a . (4) 作出判断: 代入样本观测值,若统计量观测值落入拒绝域 W1 则拒绝原假设;否则接受原假设. 上述步骤也同样适用于非参数检验,如关于分布的检验和独立性检验.只不过分布的检验和 独立性检验都是以 2 x 分布为检验统计量并且都是单侧检验

最后需要说明的是,假设检验是根据小概率事件原理进行推断的但是一个发生可能性很小 的事件也并非是绝对不可能发生的,因此我们的检验也可能出现错误,即第一类错误一一 H。为真时却拒绝了H。,其概率为显著性水平α,或第二类错误一一H。为假时却接受了 H。,其概率为B 单个总体,方差已知时,均值的检验 问题设总体5~N(山,o2),己知其中O=O。,(X,X2,…,X,)是5的样本, 要检验H。:4=4o。 检验方法 X-上n一N0,),从样本可以算出U的值,定出一个值“%,称为临界值, 00 把U的取值范围分成两个区域:。={UU≤4%}和形={UW>“%。称 W。为接受域,称W,为拒绝域。从样本求出U的值,U的值落在W。中,就接受H。,U的 值落在W中,就拒绝H。。 单个总体,方差未知时,均值的检验 问题设总体5N(4,σ2),其中O>0未知,(X,X2,…,Xn)是5的样本,要 检验Ho:I=o· 检验方法 T-X-4n==4n~m-) S* S* 从样本求出T=-凸万的值。对于给定的显著水平口,自由度n-1,查1分 S* 布表可得1分布的临界值以n-),使得PT>4-%n-1}=a,当 |T>t以n-)时拒绝H,,否则接受H,。 怎样查表求1分布的临界值 在书后附录中,有一个1分布的临界值表,从中可以查到1分布的临界值。查表时, 在自由度k=n-1与p=1-a网2的相交处可以查到1以n-)。 96
96 最后需要说明的是,假设检验是根据小概率事件原理进行推断的.但是一个发生可能性很小 的事件也并非是绝对不可能发生的,因此我们的检验也可能出现错误,即第一类错误—— H0 为真时却拒绝了 H0 ,其概率为显著性水平α,或第二类错误—— H0 为假时却接受了 H0 ,其概率为 . 单个总体,方差已知时,均值的检验 问题 设总体 ~ ( , ) 2 N ,已知其中 = 0 ,( , , , ) X1 X2 Xn 是 的样本, 要检验 H0 : = 0 。 检验方法 n X 0 − ~ N(0, 1),从样本可以算出 U 的值,定出一个值 2 u 1− ,称为临界值, 把 U 的取值范围分成两个区域: { } 2 1 W0 = U U u − 和 { } 2 1 W1 = U U u − 。称 W0 为接受域,称 W1 为拒绝域。从样本求出 U 的值, U 的值落在 W0 中,就接受 H0 ,U 的 值落在 W1 中,就拒绝 H0 。 单个总体,方差未知时,均值的检验 问题 设总体 ~ ( , ) 2 N ,其中 0 未知, ( , , , ) X1 X2 Xn 是 的样本,要 检验 H0 : = 0 。 检验方法 n S X T * − 0 = = n S X * − ~t(n −1) 。 从样本求出 n S X T * − 0 = 的值。对于给定的显著水平 ,自由度 n −1 ,查 t 分 布表可得 t 分 布 的 临 界值 ( 1) 2 1 − − t n ,使得 − = − { ( 1)} 2 1 P T t n , 当 ( 1) 2 1 − − T t n 时拒绝 H0 ,否则接受 H0 。 怎样查表求 t 分布的临界值 在书后附录中,有一个 t 分布的临界值表,从中可以查到 t 分布的临界值。查表时, 在自由度 k = n −1 与 p =1− 2 的相交处可以查到 ( 1) 2 1 − − t n

单个总体,均值未知时,方差的检验 问题设总体5~N(山,o2),其中4未知,(X,X2,…,Xn)是5的样本,要检验 H。:o2=o(或o=o0)。 检验方法 因此可得到检验方法如下: 从样本求出X2=n ,的值。对于给定的显著水平,自由度n-1,查表可得x2 0 分布的临界值gn-)和公gm-),使得P叫X父2<n-》=号以及 P叫父产>z不以a-明=号,当2<以a-)或父>xgm-)时拒绝H。, 否则接受H。。 怎样查表求X2分布的临界值 在书后附录中,有x2分布的临界值表,从中可以查到x2分布的临界值。查表时, (1)在自由度k=n-1与p=2的相交处可以查到Xg(n-): (2)在自由度k=n-1与p=1-a2的相交处可以查到X以n-)。 两个总体,方差未知但相等时,均值是否相等的检验 问题设总体5~N(41,O),刀~N(山2,σ2),其中O1,O2都未知,但已知 O1=O2,(X1,X2,…,Xm),(Y,Y2,…,Yn)分别是5,7的样本,两个样本相互独 立,要检验H。:=42。 检验方法 检验方法如下: 从样本求出T= x-7 的值。对于给定的显著水平a,自由度m+n-2,查 11 S.\m n 表可求得1分布的临界值1-%m+n-2),使得PT>1-%m+n-2}=a,当 97
97 单个总体,均值未知时,方差的检验 问题 设总体 ~ ( , ) 2 N ,其中 未知, ( , , , ) X1 X2 Xn 是 的样本,要检验 H0 : 2 0 2 = (或 = 0 ) 。 检验方法 因此可得到检验方法如下: 从样本求出 2 0 2 2 nS = 的值。对于给定的显著水平 ,自由度 n −1 ,查表可得 2 分 布 的 临界 值 ( 1) 2 2 n − 和 ( 1) 2 2 1 − − n , 使得 2 { ( 1)} 2 2 2 P n − = 以 及 2 { ( 1)} 2 2 1 2 − = − P n ,当 ( 1) 2 2 2 n − 或 ( 1) 2 2 1 2 − − n 时拒绝 H0 , 否则接受 H0 。 怎样查表求 2 分布的临界值 在书后附录中,有 2 分布的临界值表,从中可以查到 2 分布的临界值。查表时, (1)在自由度 k = n −1 与 p = 2 的相交处可以查到 ( 1) 2 2 n − ; (2)在自由度 k = n −1 与 p =1− 2 的相交处可以查到 ( 1) 2 2 1 − − n 。 两个总体,方差未知但相等时,均值是否相等的检验 问题 设总体 ~ ( , ) 2 N 1 1 , ~ ( , ) 2 N 2 2 ,其中 1, 2 都未知,但已知 1 = 2 ,( X X X m , , , 1 2 ) ,( Y Y Yn , , , 1 2 )分别是 , 的样本,两个样本相互独 立,要检验 H0 : 1= 2 。 检验方法 检验方法如下: 从样本求出 m n S X Y T w 1 1 + − = 的值。对于给定的显著水平 ,自由度 m + n − 2 ,查 表可求得 t 分布的临界值 ( 2) 2 1 + − − t m n ,使得 + − = − { ( 2)} 2 1 P T t m n ,当