
《抽象代数》课程教学大纲 一、课程信息 课程名称:抽象代数 Abstract Algebra 课程代码:06S1114B 课程类别:专业核心课程/必修课 适用专业:数学与应用数学 课程学时:64学时 课程学分:4学分 修读学期:第5学期 先修课程:高等代数1、高等代数2 二、课程目标 抽象代数以群、环、域等代数系统为其基本内容。它对高等代数中出现的数 域、多项式、矩阵、线性空间等概念进一步概括,具有抽象的特点,适宜于培养 学生抽象思维和逻辑推理的能力。它不仅是将来学习代数的一个入门,而且与其 它学科,如几何、拓扑、泛函和有限数学等有密切联系。抽象代数主要讲授群、 环、域的基本概念、基本理论、基本性质等。群方面介绍变换群、置换群、循环 群、正规子群、商群、群同态、n元交错群等;环方面介绍模n剩余类环、多项式 环、理想、商环、同态及同构等。域方面介绍域的基本定理、基本性质。先修课 程为高等代数等课程。 (一)具体目标 通过本课程的学习,使学生达到以下目标: 1.深刻理解群(半群、子群)、环(子环、理想)、域等基本概念;熟练掌握 些群(循环群、置换群、变换群、一般线性群等),环(整环、除环、模n剩余类环 、多项式环等),域(有理分式域等)的概念以及相关概念(运算与运算律、等价关 系与集合的分类、群的同态与同构、环的同态与同构、正规子群与商群、理想 与商环、环的特征、单位群等)。【支撑毕业要求指标点3.1、3.2、3.3】
《抽象代数》课程教学大纲 一、课程信息 课程名称:抽象代数 Abstract Algebra 课程代码:06S1114B 课程类别:专业核心课程/必修课 适用专业:数学与应用数学 课程学时:64学时 课程学分:4学分 修读学期:第5学期 先修课程:高等代数1、高等代数2 二、课程目标 抽象代数以群、环、域等代数系统为其基本内容。它对高等代数中出现的数 域、多项式、矩阵、线性空间等概念进一步概括,具有抽象的特点,适宜于培养 学生抽象思维和逻辑推理的能力。它不仅是将来学习代数的一个入门,而且与其 它学科,如几何、拓扑、泛函和有限数学等有密切联系。抽象代数主要讲授群、 环、域的基本概念、基本理论、基本性质等。群方面介绍变换群、置换群、循环 群、正规子群、商群、群同态、n元交错群等;环方面介绍模n剩余类环、多项式 环、理想、商环、同态及同构等。域方面介绍域的基本定理、基本性质。先修课 程为高等代数等课程。 (一)具体目标 通过本课程的学习,使学生达到以下目标: 1. 深刻理解群(半群、子群)、环(子环、理想)、域等基本概念;熟练掌握一 些群(循环群、置换群、变换群、一般线性群等),环(整环、除环、模n剩余类环 、多项式环等),域(有理分式域等)的概念以及相关概念(运算与运算律、等价关 系与集合的分类、群的同态与同构、环的同态与同构、正规子群与商群、理想 与商环、环的特征、单位群等)。【支撑毕业要求指标点3.1、3.2、3.3】
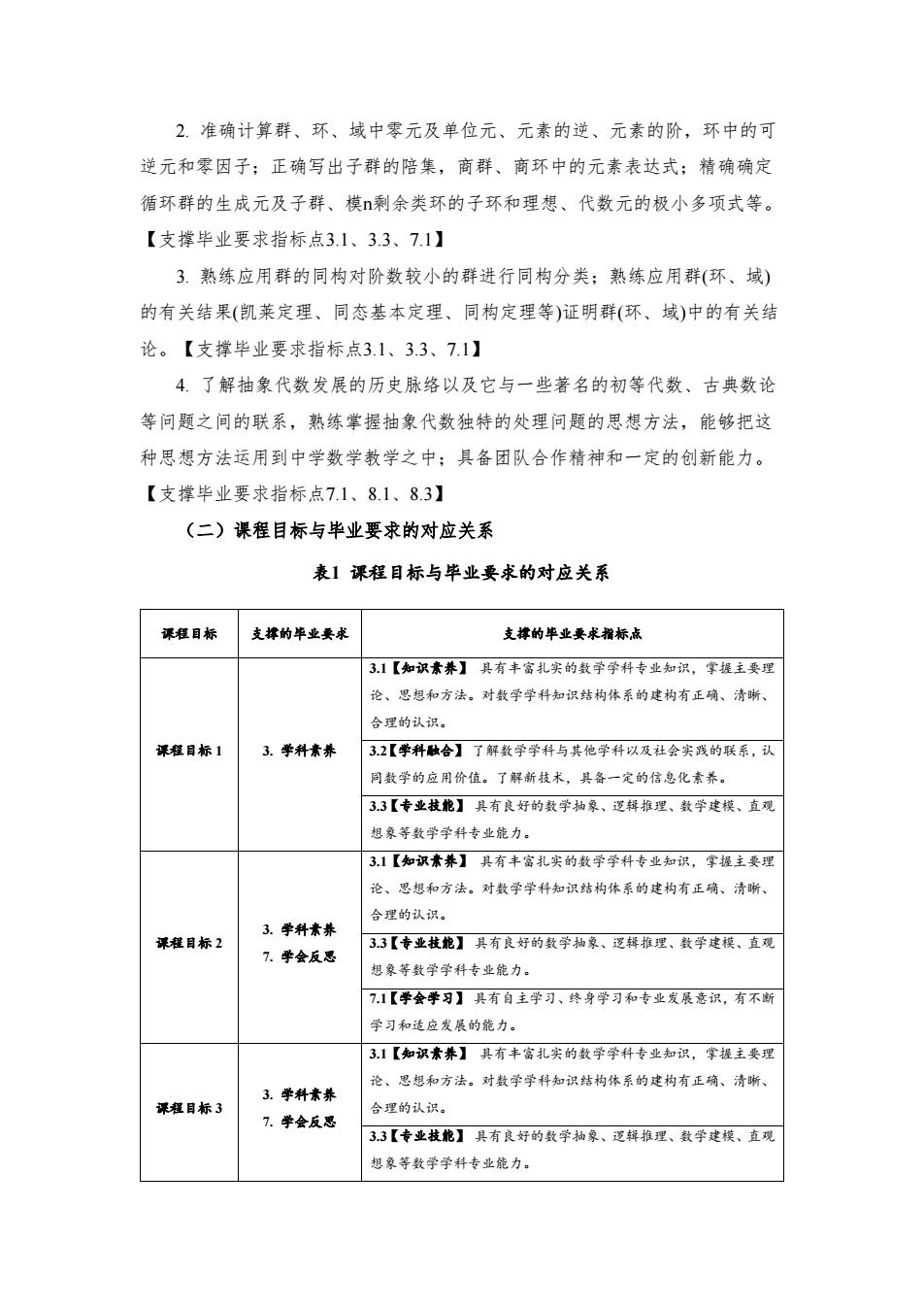
2.准确计算群、环、域中零元及单位元、元素的逆、元素的阶,环中的可 逆元和零因子;正确写出子群的陪集,商群、商环中的元素表达式;精确确定 循环群的生成元及子群、模剩余类环的子环和理想、代数元的极小多项式等。 【支撑毕业要求指标点3.1、3.3、7.1】 3.熟练应用群的同构对阶数较小的群进行同构分类;熟练应用群(环、域) 的有关结果(凯莱定理、同态基本定理、同构定理等)证明群(环、域)中的有关结 论。【支撑毕业要求指标点3.1、3.3、7.1】 4.了解抽象代数发展的历史脉络以及它与一些著名的初等代数、古典数论 等问题之间的联系,熟练掌握抽象代数独特的处理问题的思想方法,能够把这 种思想方法运用到中学数学教学之中;具备团队合作精神和一定的创新能力。 【支撑毕业要求指标点7.1、8.1、8.3】 (二)课程目标与毕业要求的对应关系 表1课程目标与毕业要求的对应关系 课程目标 支撑的毕业要求 支撑的毕业要求指标底 3.1【知识素养】具有丰富扎实的数学学科专业知识,掌握主要理 论、思想和方法。对数学学科知识结构体系的建构有正确、清晰、 合理的认识。 课程目标1 3.学科素养 3.2【学科融合】了解数学学科与其他学科以及社会实践的联系,认 同数学的应用价值。了解新技术,具备一定的信息化素养。 3.3【专业技舵】具有良好的数学抽象、逻辑推理、数学建模、直规 想象等数学学科专业能力。 3.1【知识素养】具有丰富扎实的数学学科专业知识,掌握主要理 论、思想和方法。对数学学科知识结构体系的建构有正确、清晰、 合理的认识。 3.学科素养 课程目标2 3.3【专业技能】具有良好的数字抽象、逻辑推理、数学建模、直观 7.学会反思 想象等数学学科专业能力。 7.1【学会学习】具有自主学习、终身学习和专业发展意识,有不断 学习和适应发展的能力。 3.1【知识素养】具有丰富扎实的数学学科专业知识,掌提主要理 论、思想和方法。对数学学科知识结构体系的建构有正确、清晰、 3.学科素并 评程目标3 合理的认识。 7.学会反思 3.3【专业技能】具有良好的数学抽象、逻辑推理、数学建模、直观 想象等数学学科专业能力
2. 准确计算群、环、域中零元及单位元、元素的逆、元素的阶,环中的可 逆元和零因子;正确写出子群的陪集,商群、商环中的元素表达式;精确确定 循环群的生成元及子群、模n剩余类环的子环和理想、代数元的极小多项式等。 【支撑毕业要求指标点3.1、3.3、7.1】 3. 熟练应用群的同构对阶数较小的群进行同构分类;熟练应用群(环、域) 的有关结果(凯莱定理、同态基本定理、同构定理等)证明群(环、域)中的有关结 论。【支撑毕业要求指标点3.1、3.3、7.1】 4. 了解抽象代数发展的历史脉络以及它与一些著名的初等代数、古典数论 等问题之间的联系,熟练掌握抽象代数独特的处理问题的思想方法,能够把这 种思想方法运用到中学数学教学之中;具备团队合作精神和一定的创新能力。 【支撑毕业要求指标点7.1、8.1、8.3】 (二)课程目标与毕业要求的对应关系 表1 课程目标与毕业要求的对应关系 课程目标 支撑的毕业要求 支撑的毕业要求指标点 课程目标 1 3. 学科素养 3.1【知识素养】 具有丰富扎实的数学学科专业知识,掌握主要理 论、思想和方法。对数学学科知识结构体系的建构有正确、清晰、 合理的认识。 3.2【学科融合】 了解数学学科与其他学科以及社会实践的联系,认 同数学的应用价值。了解新技术,具备一定的信息化素养。 3.3【专业技能】 具有良好的数学抽象、逻辑推理、数学建模、直观 想象等数学学科专业能力。 课程目标 2 3. 学科素养 7. 学会反思 3.1【知识素养】 具有丰富扎实的数学学科专业知识,掌握主要理 论、思想和方法。对数学学科知识结构体系的建构有正确、清晰、 合理的认识。 3.3【专业技能】 具有良好的数学抽象、逻辑推理、数学建模、直观 想象等数学学科专业能力。 7.1【学会学习】 具有自主学习、终身学习和专业发展意识,有不断 学习和适应发展的能力。 课程目标 3 3. 学科素养 7. 学会反思 3.1【知识素养】 具有丰富扎实的数学学科专业知识,掌握主要理 论、思想和方法。对数学学科知识结构体系的建构有正确、清晰、 合理的认识。 3.3【专业技能】 具有良好的数学抽象、逻辑推理、数学建模、直观 想象等数学学科专业能力
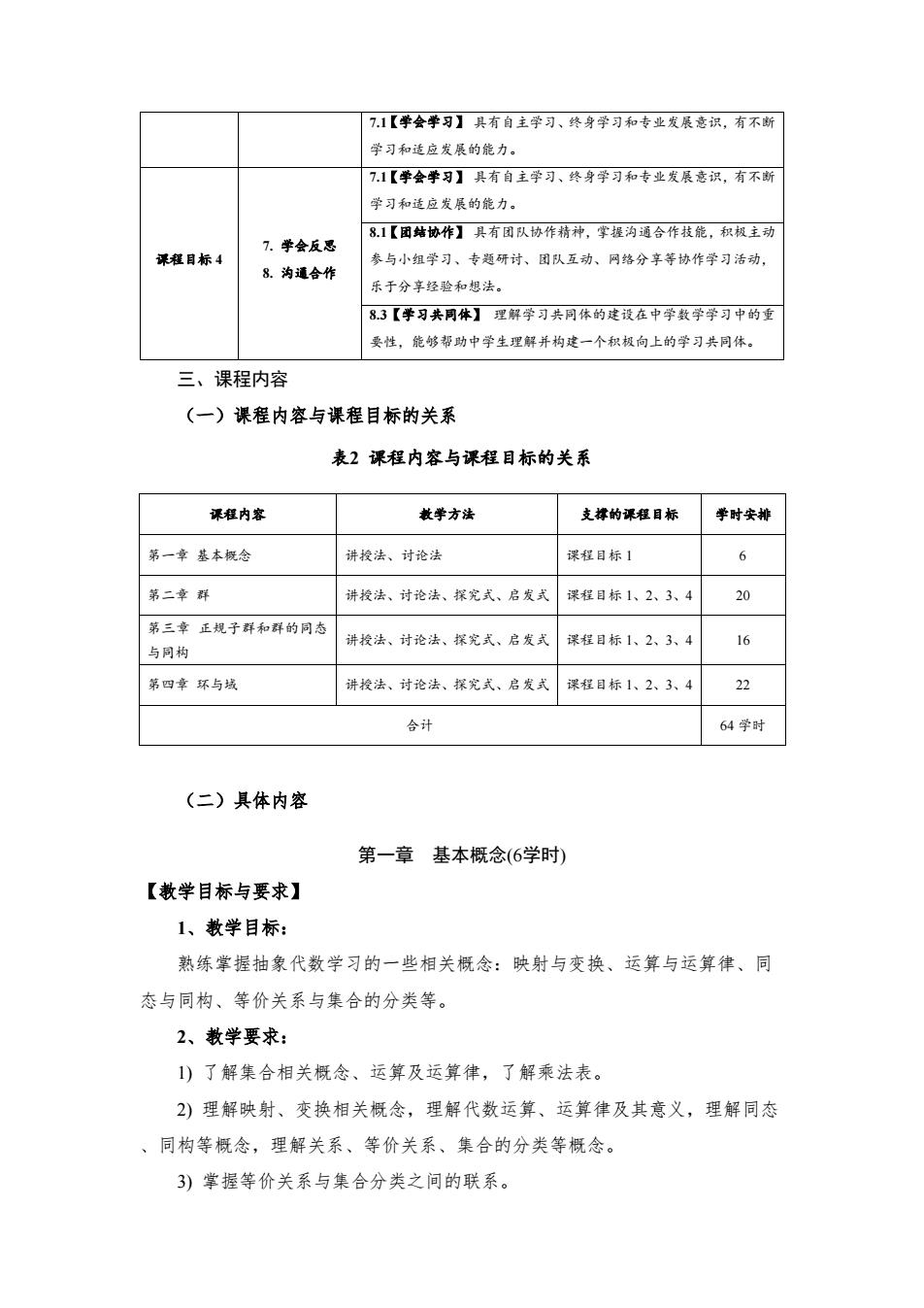
71【学会学习】具有自主学习、终身学习和专业发展意识,有不断 学习和适应发展的能力。 7.1【学会学习】具有自主学习、终身学习和专业发展意识,有不断 学习和适应发展的能力。 81【田结协作】具有团队协作精神,掌握沟通合作技能,积极主动 7学会反思 评椎目标4 参与小组学习、专题研讨、团队互动、网络分享等协作学习活动, 8.沟道合作 乐于分享经验和想法。 8.3【学习共同体】理解学习共同体的建设在中学数学学习中的重 要性,能够帮助中学生理解并构建一个积极向上的学习共同体。 三、课程内容 (一)课程内容与课程目标的关系 表2课程内容与课程目标的关系 课程内容 教学方法 支撑的课程目标 学时安排 第一章基本概念 讲授法、讨论法 课程目标1 6 第二章群 讲授法、讨论法、探究式、启发式 课程目标1、2、3、4 20 第三章正规子群和群的同态 讲授法、讨论法、探究式、启发式 课程目标1、2、3、4 16 与同构 第四章环与域 讲授法、讨论法、探究式、启发式 课程目标1、2、3、4 22 合计 64学时 (二)具体内容 第一章基本概念(6学时) 【教学目标与要求】 1、教学目标: 熟练掌握抽象代数学习的一些相关概念:映射与变换、运算与运算律、同 态与同构、等价关系与集合的分类等。 2、教学要求: 1)了解集合相关概念、运算及运算律,了解乘法表。 2)理解映射、变换相关概念,理解代数运算、运算律及其意义,理解同态 、同构等概念,理解关系、等价关系、集合的分类等概念。 3)掌握等价关系与集合分类之间的联系
7.1【学会学习】 具有自主学习、终身学习和专业发展意识,有不断 学习和适应发展的能力。 课程目标 4 7. 学会反思 8. 沟通合作 7.1【学会学习】 具有自主学习、终身学习和专业发展意识,有不断 学习和适应发展的能力。 8.1【团结协作】 具有团队协作精神,掌握沟通合作技能,积极主动 参与小组学习、专题研讨、团队互动、网络分享等协作学习活动, 乐于分享经验和想法。 8.3【学习共同体】 理解学习共同体的建设在中学数学学习中的重 要性,能够帮助中学生理解并构建一个积极向上的学习共同体。 三、课程内容 (一)课程内容与课程目标的关系 表2 课程内容与课程目标的关系 课程内容 教学方法 支撑的课程目标 学时安排 第一章 基本概念 讲授法、讨论法 课程目标 1 6 第二章 群 讲授法、讨论法、探究式、启发式 课程目标 1、2、3、4 20 第三章 正规子群和群的同态 与同构 讲授法、讨论法、探究式、启发式 课程目标 1、2、3、4 16 第四章 环与域 讲授法、讨论法、探究式、启发式 课程目标 1、2、3、4 22 合计 64 学时 (二)具体内容 第一章 基本概念(6学时) 【教学目标与要求】 1、教学目标: 熟练掌握抽象代数学习的一些相关概念:映射与变换、运算与运算律、同 态与同构、等价关系与集合的分类等。 2、教学要求: 1) 了解集合相关概念、运算及运算律,了解乘法表。 2) 理解映射、变换相关概念,理解代数运算、运算律及其意义,理解同态 、同构等概念,理解关系、等价关系、集合的分类等概念。 3) 掌握等价关系与集合分类之间的联系

【教学重点与难点】 1、教学重点:代数运算、同态与同构。 2、教学难点:等价关系与集合分类的联系。 【教学内容】 1.1集合 1.4运算律 1.2映射与变换 1.5同态与同构 1.3代数运算 1.6等价关系与集合的分类 【思政元素融入点】 在概念和定理的引入时融入科学家故事,培养学生勤奋钻研的科学精神。 同一个剩余类有多种表示形式,能体现事物表现形式多样性,可以引出“现象 与本质”的辩证关系,引导学生深入思考,抓住事物的本质。每个剩余类的元 素都有无限个,每个元素都可以作为代表,可以引出社会主义核心价值观中的 “民主,平等”,培养学生的爱国主义情怀,从而发奋图强,努力学习,为国 争光。 第二章群(20学时) 【教学目标与要求】 1、教学目标: 深刻理解群(半群、子群)等基本概念,熟练掌握一些群(循环群、置换群、 变换群、一般线性群等)的概念以及相关概念(群的同态与同构、陪集等)。准确 计算群中单位元、元素的逆、元素的阶,正确写出子群的陪集,精确确定循环 群的生成元及子群。熟练应用凯莱定理证明群中的有关结论。了解抽象代数发 展的历史脉络以及它与一些著名的初等代数、古典数论等问题之间的联系,初 步掌握近世代数独特的处理问题的思想方法,能够把这种思想方法运用到中学 数学教学之中;具备团队合作精神和一定的创新能力。 2、教学要求: 1)理解群和半群的定义,掌握群的性质,熟知群和半群的一些典型实例。 2)理解元素阶的定义,掌握元素阶的性质。 3)理解子群、中心、集合的乘积等定义,掌握子群的判断方法,了解子群 的交、并、积还是否为子群
【教学重点与难点】 1、教学重点:代数运算、同态与同构。 2、教学难点:等价关系与集合分类的联系。 【教学内容】 1.1 集合 1.4 运算律 1.2 映射与变换 1.5 同态与同构 1.3 代数运算 1.6 等价关系与集合的分类 【思政元素融入点】 在概念和定理的引入时融入科学家故事,培养学生勤奋钻研的科学精神。 同一个剩余类有多种表示形式,能体现事物表现形式多样性,可以引出“现象 与本质”的辩证关系,引导学生深入思考,抓住事物的本质。每个剩余类的元 素都有无限个,每个元素都可以作为代表,可以引出社会主义核心价值观中的 “民主,平等”,培养学生的爱国主义情怀,从而发奋图强,努力学习,为国 争光。 第二章 群(20学时) 【教学目标与要求】 1、教学目标: 深刻理解群(半群、子群)等基本概念,熟练掌握一些群(循环群、置换群、 变换群、一般线性群等)的概念以及相关概念(群的同态与同构、陪集等)。准确 计算群中单位元、元素的逆、元素的阶,正确写出子群的陪集,精确确定循环 群的生成元及子群。熟练应用凯莱定理证明群中的有关结论。了解抽象代数发 展的历史脉络以及它与一些著名的初等代数、古典数论等问题之间的联系,初 步掌握近世代数独特的处理问题的思想方法,能够把这种思想方法运用到中学 数学教学之中;具备团队合作精神和一定的创新能力。 2、教学要求: 1) 理解群和半群的定义,掌握群的性质,熟知群和半群的一些典型实例。 2) 理解元素阶的定义,掌握元素阶的性质。 3) 理解子群、中心、集合的乘积等定义,掌握子群的判断方法,了解子群 的交、并、积还是否为子群

4)理解生成系和循环群的定义,了解循环群中元素的表示,掌握循环群的 生成元、子群的情况,知道在同构的意义下循环群只有两类。 5)了解变换群的定义,理解双射变换群中只能含有单射和满射,理解 Cayley定理。 6)了解置换群的定义,掌握置换的运算、表示,知道置换的阶和逆,掌握 置换群中奇偶置换的情况。 7)理解左右陪集、指数的定义和lagrange定理,掌握陪集的性质,知道陪 集分解及其关系。 【教学重点与难点】 1、教学重点:群、子群、循环群、置换群、陪集的概念和基本性质。 2、教学难点:变换群。 【教学内容】 2.1群的定义和初步性质 2.5变换群 2.2群中元素的阶 2.6置换群 2.3子群 2.7陪集、指数和Lagrange定理 2.4循环群 【思政元素融入点】 在概念和定理的引入时融入科学家故事,培养学生勤奋钻研的精神。由群 与群的例子引出“抽象和具体”、“普遍与特殊”的辩证关系。由群与子群的 关系引出“整体与部分”的辩证关系:整体由部分组成,居于主导地位,具有 部分不具备的功能,部分制约整体,关键部分甚至对整体的功能起决定作用。 由置换群引出对称群、对称、对称美,引导学生认识图形的对称美、诗词及对 联中文字及意境的对称美等。 第三章正规子群和群的同态与同构(16学时) 【教学目标与要求】 1、教学目标: 熟练掌握群的同态与同构、正规子群与商群等概念。正确写出商群中的元 素表达式。熟练应用群的同构对阶数较小的群进行同构分类,熟练应用群同态 基本定理、同构定理等证明群中的有关结论。了解抽象代数发展的历史脉络以
4) 理解生成系和循环群的定义,了解循环群中元素的表示,掌握循环群的 生成元、子群的情况,知道在同构的意义下循环群只有两类。 5) 了解变换群的定义,理解双射变换群中只能含有单射和满射,理解 Cayley定理。 6) 了解置换群的定义,掌握置换的运算、表示,知道置换的阶和逆,掌握 置换群中奇偶置换的情况。 7) 理解左右陪集、指数的定义和lagrange定理,掌握陪集的性质,知道陪 集分解及其关系。 【教学重点与难点】 1、教学重点:群、子群、循环群、置换群、陪集的概念和基本性质。 2、教学难点:变换群。 【教学内容】 2.1 群的定义和初步性质 2.5 变换群 2.2 群中元素的阶 2.6 置换群 2.3 子群 2.7 陪集、指数和Lagrange定理 2.4 循环群 【思政元素融入点】 在概念和定理的引入时融入科学家故事,培养学生勤奋钻研的精神。由群 与群的例子引出“抽象和具体”、“普遍与特殊”的辩证关系。由群与子群的 关系引出“整体与部分”的辩证关系:整体由部分组成,居于主导地位,具有 部分不具备的功能,部分制约整体,关键部分甚至对整体的功能起决定作用。 由置换群引出对称群、对称、对称美,引导学生认识图形的对称美、诗词及对 联中文字及意境的对称美等。 第三章 正规子群和群的同态与同构(16学时) 【教学目标与要求】 1、教学目标: 熟练掌握群的同态与同构、正规子群与商群等概念。正确写出商群中的元 素表达式。熟练应用群的同构对阶数较小的群进行同构分类,熟练应用群同态 基本定理、同构定理等证明群中的有关结论。了解抽象代数发展的历史脉络以