
第7章 统计假设检脸和区间估计 统计假设检验概要 ·单正态总体的统计检验 两正态总体的统计检验 正态总体的区间估计 需要说明的问题
•统计 检验概要 •单正态总体的统计检验 •两正态总体的统计检验 •需要说明的问题 •正态总体的区间估计

统计检验概要 利用样本检验统计假设真伪的过程叫做 统计检验(假设检验) 1.统计检验的基本思想 (1)小概率原理(实际推断原理)认为概率很小的事件在 次试验中实际上不会出现,并且小概率事件在一次试验中 出现了,就被认为是不合理的 (2)基本思想先对总体的参数或分布函数的表达式做出某 种假设,然后找出一个在假设成立条件下出现可能性甚小 的(条件)小概率事件.如果试验或抽样的结果使该小概率 事件出现了,表明原来的假设有问题,应予以否定,即拒绝 这个假设.若该小概率事件在一次试验或抽样中并未出现, 就没有理由否定这个假设,可以接受原来的假设
(1)小概率原理(实际推断原理)认为概率很小的事件在一 次试验中实际上不会出现,并且小概率事件在一次试验中 出现了,就被认为是不合理的. (2)基本思想 先对总体的参数或分布函数的表达式做出某 种假设,然后找出一个在假设成立条件下出现可能性甚小 的(条件)小概率事件.如果试验或抽样的结果使该小概率 事件出现了, 表明原来的假设有问题,应予以否定,即拒绝 这个假设.若该小概率事件在一次试验或抽样中并未出现, 就没有理由否定这个假设, 可以接受原来的假设. 1.统计检验的基本思想 统计检验概要 利用样本检验统计假设真伪的过程叫做 统计检验(假设检验)

(3)显著性水平与否定域 小概率原理中,关于“小概率”的值通常根据实际问题的 要求而定,如取a=0.1,0.05,0.01等 a为检验的显著性水平(检验水平):
小概率原理中,关于“小概率”的值通常根据实际问题的 要求而定,如取α=0.1,0.05,0.01等, α为检验的显著性水平(检验水平). (3) 显著性水平与否定域
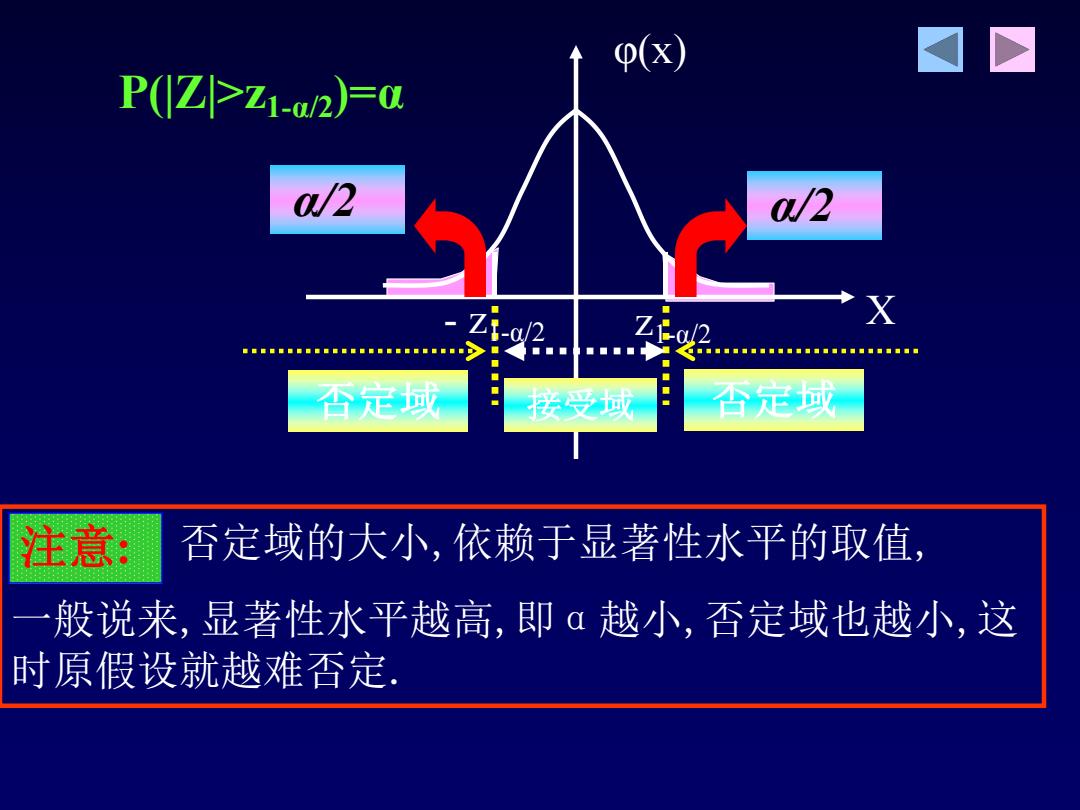
o(x) P(ZPz1-w2)戶a /2 /2 Z1-c2 Zt-al2 X 否定成 ◆ 安受或 否足或 注意: 否定域的大小,依赖于显著性水平的取值, 一般说来,显著性水平越高,即α越小,否定域也越小,这 时原假设就越难否定
α/2 α/2 X φ(x) 接受域 P(|Z|>z1-α/2)=α 否定域的大小,依赖于显著性水平的取值, 一般说来,显著性水平越高,即α越小,否定域也越小,这 时原假设就越难否定. 注意: 否定域 否定域 z1-α/2 - z1-α/2

2.统计检验的实施程序 1) 提出待检验的原假设H和备则假设H,; (2)选择检验统计量,并找出在假设H。 成立条件下,该统计量所服从的分布, (3)根据所要求的显著性水平α和所选取的统计量,确定 个合理的拒绝H的条件, (4) 由样本观察值计算出统计检验量的值,若该值落入否 定域,则拒绝原假设H,否则接受原假设H。 注若H位于H的两侧,称之为双侧检验, 若H位于H的一侧,称之为单侧检验
(1) 提出待检验的原假设 和备则假设 ; H0 H1 (2) 选择检验统计量,并找出在假设 成立条件下,该统计量所服从的分布; H0 (3) 根据所要求的显著性水平α 和所选取的统计量,确定一 个合理的拒绝H0的条件; (4) 由样本观察值计算出统计检验量的值,若该值落入否 定域,则拒绝原假设H0,否则接受原假设 . H0 注 若H1位于H0的两侧,称之为双侧检验; 若H1位于H0的一侧,称之为单侧检验. 2.统计检验的实施程序