西安电子科技大学：《矩阵论》研究生课程教学课件（讲义，2014）15 Penrose广义逆的性质

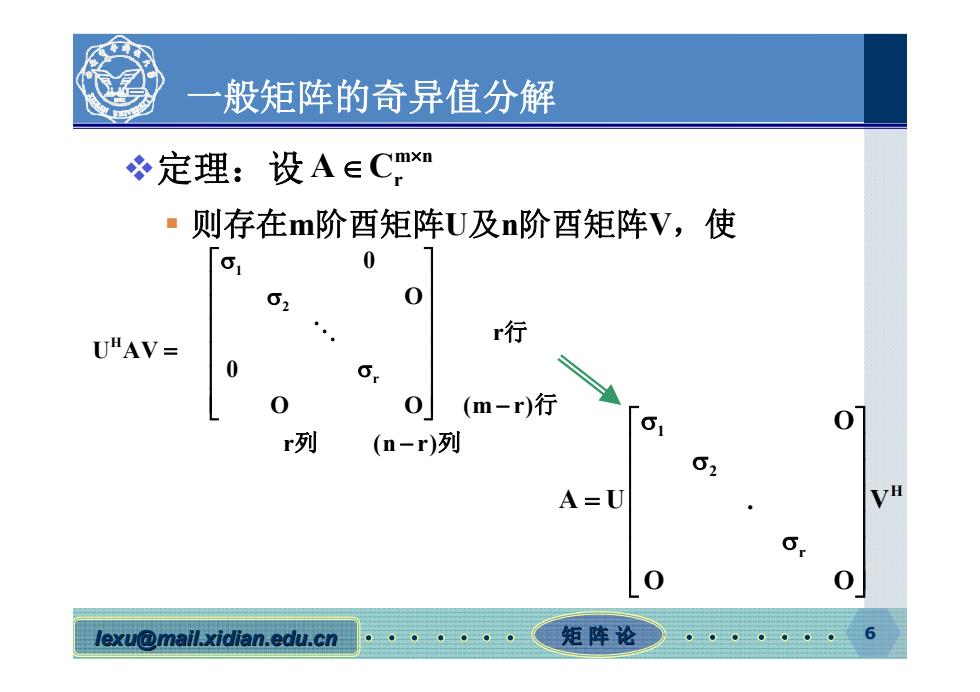
一 般矩阵的奇异值分解 定理：设A∈Cm知 ·则存在m阶酉矩阵U及n阶酉矩阵V,使 0 r行 UHAV= 0 0(m-r)行 6 r列 (n-r)列 62 A=U lexu@mail.xidian.edu.cn 矩阵论

lexu @mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 6 一般矩阵的奇异值分解 定理：设  则存在 m阶酉矩阵 U 及 n阶酉矩阵 V ， 使 m n A C r   1 2 H r 0 O r U AV 0 O O (m r) r (n r)                       行 行 列 列 1 2 H r O AU V . O O                    

o 01 V= [V I V] r列(n-r)列 VH(AHA)V= 0 令U1=AV∑ 冬由基扩充定理可知，可在U,的基础上构造酉 矩阵U=[UU2] lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 由基扩充定理可知,可在Ｕ１的基础上构造酉 矩阵Ｕ＝[U1|U2] 7 2 1 2 2 H H 2 r n n O V (A A)V . O O                     V |V 1 2  V r (n r)  列 列 

Penrose 广义逆 必何谓广义 ·即推广了原有概念或结果 逆矩阵一般概念 ·针对非奇异的（或称为满秩的)方阵 ·这一概念可推广到 ·奇异方阵 ·非方矩阵 ·事实上，Penrose)广义逆矩阵涵盖了两种情况 lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 8 Penrose 广义逆 何谓广义  即推广了原有概念或结果 逆矩阵一般概念  针对非奇异的（或称为满秩的）方阵  这一概念可推广到 • 奇异方阵 • 非方矩阵 • 事实上， Penrose广义逆矩阵涵盖了两种情况

Penrose 广义逆 Penrose定义 .设A∈Cmxm,若Z∈Cxm且使如下四个等式成立 AZA=A,ZAZ=Z,(AZ)=AZ,(ZA)=ZA ·则称Z为A的Moore-Penrose(广义)逆 ·记为A+ ■上述四个等式又依次称为Penrose方程（i一iv) Moore-.Penrose逆的存在性和唯一性 ·定理：任给A∈Cmm，A*均存在且唯一 A=UDVH Z=VDUE lexu@mail.xidian.edu.cn 矩阵论

lexu@mail.xidian.edu.cn mail.xidian.edu.cn 矩 阵 论 9 Penrose 广义逆 Penrose定义   则称Z为A的Moore-Penrose(广义)逆  记为A＋  上述四个等式又依次称为Penrose方程（i－iv)  Moore-Penrose逆的存在性和唯一性  定理：