《线性代数》课程教学课件（PPT讲稿，A）5-5 二次型及其标准形

只含有平方项的二次型f=ay+ay+..+ay称为二次型的标准型，所以：因为标准二次型只含平方项，221.标准二次型的矩阵是对角矩阵人2.要使二次型f经可逆变换x=Cy变成标准形就是要使y'CACy=a?+ay+...+any也就是要使CAC成为对角矩阵

线性代数 第五章 2 2 2 1 1 2 2 2 , . n n . f x Cy y C ACy y y y C AC    =   = + + +  要使二次型 经可逆变换 变成标准形 就是要使 也就是要使 成为对角矩阵 1 2 1 ; n .                标准二次型的矩阵是对角矩阵 2 2 2 1 1 2 2 . n n f y y y = + + +    只含有平方项的二次型 称为二次型的标准型 因为标准二次型只含平方项，所以：

线性代数 第五章由于对任意的实对称矩阵A.总有正交矩阵P使P-AP=A，即P'AP=A.因此任意一个实二次型都可以化为标准形定义5.3.3如果线性变换X=CY的系数矩阵C-(cj)nXn是正交矩阵，则称它为正交线性变换，简称正交变换显然正交变换是可逆的

线性代数 第五章 1 , , , . A P P AP P AP − =  =   由于对任意的实对称矩阵 总有正交矩阵 使 即 因此任意一个实二次型 都可以化为标准形. 定义5.3.3 如果线性变换X=CY的系数矩阵C=(cij)n×n 是正交矩阵，则称它为正交线性变换，简称正交变换. 显然正交变换是可逆的

任给实二次型f =X'AX(A'=A)，总有定理5.5.1正交变换X=PY，使f化为标准形f=ay+y+...+ay其中,,…,,是矩阵A的特征值.例1求正交变换X=PY，把二次型f=4x+3x+2xx+3x化为标准形A01=03解:(1)二次型的矩阵为：A=03

线性代数 第五章 2 2 2 1 1 2 2 1 2 5 ( ) , , . .5.1 n n n f X AX A A X PY f f y y y A       = =   = = + + + 任给实二次型 ，总有 正交变换 ，使 化为标准形 其中 ， 是矩阵 定 的特征值 理 2 2 2 1 2 2 3 3 1 4 3 2 3 . X PY f x x x x x = = + + + 例 求正交变换 ，把二次型 化为标准形 解:(1)二次型的矩阵为： 4 0 0 0 3 1 0 1 3 A     =      

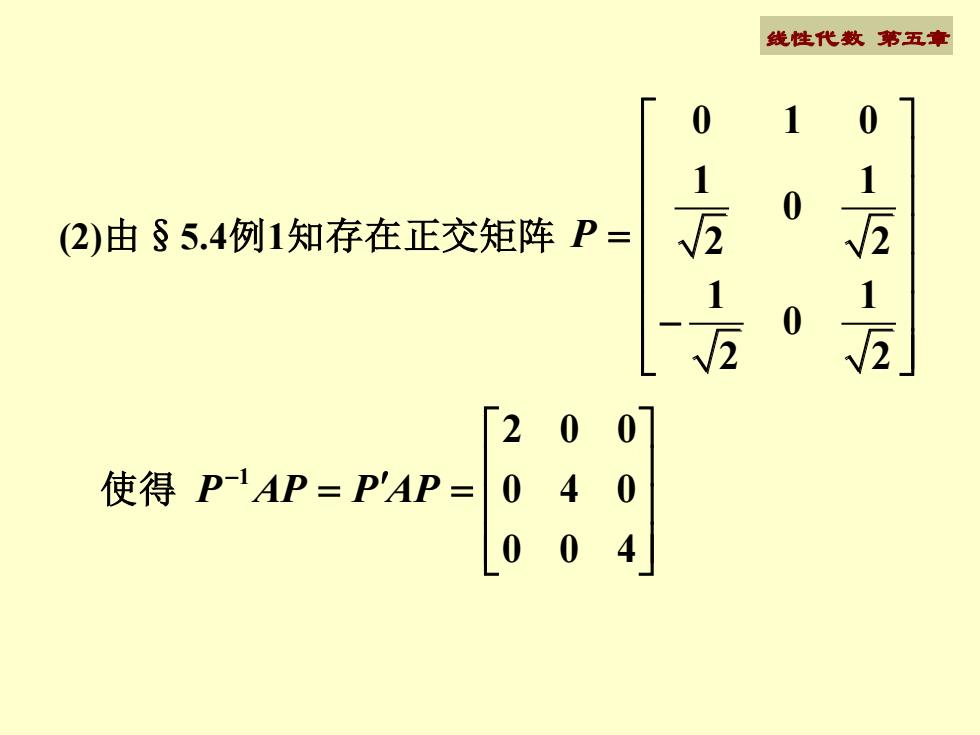
线性代数 第五享万1万2(2)由 S 5.4例1知存在正交矩阵 P=1J21使得 P-1AP=P'AP=-/11

线性代数 第五章 (2)由§5.4例1知存在正交矩阵 0 1 0 1 1 0 2 2 1 1 0 2 2 P       =       −     1 200 0 4 0 0 0 4 P AP P AP −     = =        使得

41S5.4例1设A=0313求正交矩阵P，使P-AP为对角形矩阵解(1)第一步求A的特征值04-元03-1 =(2-)(4-)20A-E=013-得特征值=2,22==4

线性代数 第五章     − − − − = 0 1 3 0 3 1 4 0 0 A E 2 = − − (2 )(4 ) ,   2, 4. 得特征值 1 = 2 = 3 = 1 4 0 0 1 0 3 1 0 1 3 . A P P AP −     =       例 设 ， 求正交矩阵 ，使 为对角形矩阵 解 (1)第一步 求A的特征值 §5.4