
第五章Advancedmathematics高等数学向量与空间解析几何人民邮电出版社
1 第五 章 向量与空间解析几何 第五章 人民邮电出版社 Advanced mathematics 高等数学 向量与空间解析几何

第五章内容导航第一节向量及其运算第二节平面及其方程第三节直线及其方程第四节曲面与曲线
2 第五 章 向量与空间解析几何 第五章 内容导航 第二节 平面及其方程 第三节 直线及其方程 第四节 曲面与曲线 第一节 向量及其运算

课前导读既有大小又有方向的物理量称为向量.在数学上可用有向线段来表示向量,其长度表示向量的大小,其方向(箭头)表示向量的方向1、向量的表示:以M为起点,MM为终点的有向线段表示的向量记为MM,,有时也用一个黑体字母(书写时,在字母上面加一箭头)来表示(见M1图5-1),如a或a图5-1
课 前 导 读 3 既有大小又有方向的物理量称为向量. 在数学上可用有向线段来表 示向量,其长度表示向量的大小,其方向(箭头)表示向量的方向. 1、向量的表示: 以 M1 为起点, M2 为终点的有向线段表示的向量记 为 M M1 2 ,有时也用一个黑体字 母(书写 时,在字母上面加一箭头)来表示(见 图 5-1),如 a 或a . M1 M2 e a 图5-1

课前导读2、向量的模:向量的大小(数学上有向线段的长度)叫做向量的模,记作al,M,M.模为1的向量称为单位向量,记作e.模为0的向量称为零向量,记作0.零向量的方向可以看作是任意方向3、向径:以原点O为始点,向一点M引向量OM,这个向量叫做点M对于点O的向径,记作r,即r=OM.4自由向量:只与大小、方向有关,而与起点无关的向量称为自由向量
课 前 导 读 4 2、向量的模: 向量的大小(数学上有向线段的长度)叫做向量的 模,记作 a , M M1 2 .模为1的向量称为单位向量,记作 e . 模为0 的向 量称为零向量,记作0 . 零向量的方向可以看作是任意方向. 3、向径: 以原点O为始点,向一点 M 引向量OM ,这个向量叫 做点M 对于点O的向径,记作r ,即r = OM . 4、自由向量:只与大小、方向有关,而与起点无关的向量称为自 由向量
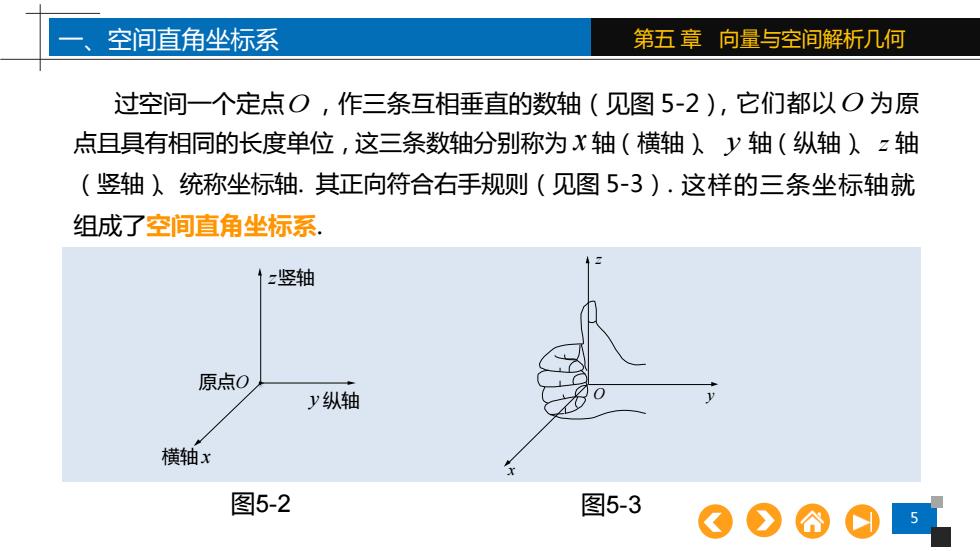
一、空间直角坐标系第五章向量与空间解析几何过空间一个定点O,作三条互相垂直的数轴(见图5-2),它们都以O为原点且具有相同的长度单位,这三条数轴分别称为x轴(横轴)V轴(纵轴)z轴(竖轴)统称坐标轴.其正向符合右手规则(见图5-3):这样的三条坐标轴就组成了空间直角坐标系1=竖轴原点01y纵轴横轴x图5-2图5-3
5 第五 章 向量与空间解析几何 过空间一个定点O,作三条互相垂直的数轴(见图 5-2), 一、空间直角坐标系 图5-2 图5-3 原点O z竖轴 y 纵轴 横轴 x O y x z 它们都以 O 为 原 点且具有相同的长度单位,这三条数轴分别称为 x 轴(横轴)、 y 轴(纵轴)、z 轴 (竖轴)、统称坐标轴. 其正向符合右手规则(见图 5-3). 这样的三条坐标轴就 组成了空间直角坐标系