
《高等数学EII》课程教学大纲一、课程的基本信息课程名称|高等数学EIAdvancedMathematicsEII课程编号L12359适用专业资源与环境学院各专业、生命与科学学院生工、生科专业课程性质公共基础课总学时80学时学分5学分理论学时80学时|实验学时0学时实践学时10学时开课学期第2学期7先修课程初等数学后续课程复变函数、线性代数、概率统计二、课程性质和课程目标1.课程性质高等数学(E)II课程是数学与统计学院大学数学教学部在资源与环境学院所有专业、生命科学学院部分专业所进行的数学公共基础课试点课程,具有较强的理论性和完整的运算体系。《高等数学(E)ⅡI》主要包括空间解析几何、多元函数的微分学、多元函数的积分学。通过本课程的学习,使学生获得高等数学的基本知识、基本思想方法和基本的运算能力,为学习后续数学课程及各专业课程打下基础。2.课程目标课程目标1正确理解高等数学(E)II中微分方程相关概念、空间解析几何相关概念、多元函数的极限、连续、偏导数、全微分、二重积分、曲线积分;了解无穷级数相关概念,把握这些概念的基本结构和隐含在其中的思想方法,并较熟练运用这些概念解决相关的问题。课程目标2通过对高等数学(E)I相关概念的性质、运算公式和定理的学习,掌握其证明思路和方法,并学会应用重要原理证明具有一定难度的问题。课程目标3熟练各种微分方程的解法,会求平面、直线、旋转曲面的方程以及空间曲线在坐标面上的投影:能够熟练运用多元函数的极限、偏导数、二重积分和曲线积分的运算方法较熟练地计算相应各类问题;会判定简单的无穷级数的收敛性
《高等数学 EII》课程教学大纲 一、课程的基本信息 课程名称 高等数学 EⅡ Advanced Mathematics EⅡ 课程编号 L12359 适用专业 资源与环境学院各专业、生命与科学学院生 工、生科专业 课程性质 公共基础课 总学时 80 学时 学分 5 学分 理论学时 80 学时 实验学时 0 学时 实践学时 0 学时 开课学期 第 2 学期 先修课程 初等数学 后续课程 复变函数、线性代数、概率统计 二、课程性质和课程目标 1.课程性质 高等数学(E)Ⅱ课程是数学与统计学院大学数学教学部在资源与环境学院 所有专业、生命科学学院部分专业所进行的数学公共基础课试点课程,具有较强 的理论性和完整的运算体系。《高等数学(E)Ⅱ》主要包括空间解析几何、多元 函数的微分学、多元函数的积分学。通过本课程的学习,使学生获得高等数学的 基本知识、基本思想方法和基本的运算能力,为学习后续数学课程及各专业课程 打下基础。 2.课程目标 课程目标 1 正确理解高等数学(E)Ⅱ中微分方程相关概念、空间解析几何相关 概念、多元函数的极限、连续、偏导数、全微分、二重积分、曲线积分;了解无 穷级数相关概念,把握这些概念的基本结构和隐含在其中的思想方法,并较熟练 运用这些概念解决相关的问题。 课程目标 2 通过对高等数学(E)Ⅱ相关概念的性质、运算公式和定理的学习, 掌握其证明思路和方法,并学会应用重要原理证明具有一定难度的问题。 课程目标 3 熟练各种微分方程的解法,会求平面、直线、旋转曲面的方程以及 空间曲线在坐标面上的投影;能够熟练运用多元函数的极限、偏导数、二重积分 和曲线积分的运算方法较熟练地计算相应各类问题;会判定简单的无穷级数的收 敛性

课程目标4熟练掌握多元函数极值的求法:掌握二重积分以及曲线积分体现的重要方法一元素法,并解决相关的总量问题。课程目标5通过高等数学(E)I中重要概念产生的背景、概念的演变过程中体现出的辩证思想、数学思想方法、历史及数学意义、数学观念和态度的了解,培养学生敢于批判、敢于质疑的勇气,培养学生追求数学的一般化、统一化的信念和理性精神。课程目标6通过对高等数学(E)ⅡI中有关概念、原理中人文因素、思政要素的分析,提升学生的人格、道德修养。三、教学内容与课程目标的对应关系与课程目序课教学设计标课程内容教学要求号时对应关系11.微分方程的1.正确理解微1.教学设计及教课程目标12基本概念分方程的定义,学建议3(1)在本章中,2.可分离变量理解微分方程不同类型的微分的微分方程的阶及解的含4.齐次微分方义;方程对应于基本程2.熟练掌握各的解法,因此在学5.一阶线性微类一阶微分方习了所有微分方分方程程的解法;程解法之后,判断6.可降解的微3.了解可降解方程的类型就成分方程的解法;的微分方程的为关键,应让学生8.高阶线性微解法;进行大量练习掌分方程解的结4.掌握线性微握判断方程类型构;分方程的解的的方法和技巧。9.常系数齐次结构;(2)突出强调本章的基本思想,即方程的解法;5.熟练掌握常10.常系数非齐系数齐次微分借助于变量代换次方程的解法。方程的解法;的方法化复杂方6.熟练掌握常程为简单方程。系数非齐次微强调在解决实际分方程的解法;问题过程中,建立微分方程模型的7.会运用微分方程解决实际重要性。问题
课程目标 4 熟练掌握多元函数极值的求法;掌握二重积分以及曲线积分体现的 重要方法—元素法,并解决相关的总量问题。 课程目标 5 通过高等数学(E)Ⅱ中重要概念产生的背景、概念的演变过程中体 现出的辩证思想、数学思想方法、历史及数学意义、数学观念和态度的了解,培 养学生敢于批判、敢于质疑的勇气,培养学生追求数学的一般化、统一化的信念 和理性精神。 课程目标 6 通过对高等数学(E)Ⅱ中有关概念、原理中人文因素、思政要素的 分析,提升学生的人格、道德修养。 三、教学内容与课程目标的对应关系 序 号 课程内容教学要求 教学设计 与课程目 标 对应关系 课 时 1 1. 微分方程的 基本概念 2.可分 离变量 的微分方程 4.齐次 微分方 程 5.一阶 线性微 分方程 6.可降 解的微 分方程的解法; 8.高阶 线性微 分方程 解的结 构; 9.常系 数齐次 方程的解法; 10.常系数非齐 次方程的解法。 1.正确理解微 分方程的定义, 理解微分方程 的阶及解的含 义; 2.熟练掌握各 类一阶微分方 程的解法; 3.了解可降解 的微分方程的 解法; 4.掌握线性微 分方程的解的 结构; 5.熟练掌握常 系数齐次微分 方程的解法; 6.熟练掌握常 系数非齐次微 分方程的解法; 7.会运用微分 方程解决实际 问题。 1.教学设计及教 学建议 (1)在本章中, 不同类型的微分 方程对应于基本 的解法,因此在学 习了所有微分方 程解法之后,判断 方程的类型就成 为关键,应让学生 进行大量练习掌 握判断方程类型 的方法和技巧。 (2)突出强调本 章的基本思想,即 借助于变量代换 的方法化复杂方 程为简单方程。 强调在解决实际 问题过程中,建立 微分方程模型的 重要性。 课程目标 3 12

1.向量的概念;1.正确理解向1.教学设计及教课程目标C162. 相量的线性学建议量的概念,熟练1运算;掌握向量加法(1)解析几何又3.空间直角坐及数与向量乘称为坐标几何或标系;积的定义、运算笛卡儿几何,这是4.向量线性运规律及其坐标数学发展史上的算的坐标表示;表示、熟记向量一座重要的里程5.向量的模、方的模、方向角的碑.解析几何的创计算公式,掌握立揭示了代数与向角、投影;6. 向量的数量向量在轴上的几何内在的联系,积与向量积;投影及其性质;为人们研究几何课程目标7.平面及其方问题或代数问题2.掌握向量积程一曲面方程和数量积的定提供了有效的研与空间曲线方义和运算规律,究方法.解析几何程的概念、平面会用数量积和诞生的科学价值向量积处理一的点法式方程、体现在以下几个方面:平面的一般方些几何问题;程、两平面的夹3.熟练掌握平1、开创了近现代角;面的一般方程、数学的先河;9.空间直线及点法式方程以2、提出了一切问课程目标其方程一间直5及截距式方程,题都可以归结为线的的一般方会求满足一定解方程问题的“通程、空间直线的条件的平面方用数学”方案,开对称式方程及程,掌握点到平创了机械化的数参数方程、两直面的距离公式,学计算方法;线的夹角、直线会判断两平面3、提出了将数学之间的位置关与平面的夹角;作为一种方法科10.曲面及其方系;学的直观一演绎程一曲面研究4.熟练掌握直法的方法论,使科课程目标的基本问题、旋线的一般方程、学方法论实现了6对称式和参数转曲面、柱面、革命性的突破;二次曲面;方程,会求满足4、为微积分诞生11.空间曲线及一定条件的直的创造了必要条件其方程一空间线方程,会判断曲线的一般方两直线及直线因此在授课过程与平面之间的程、空间曲线的中,既要穿插有关解析几何产生的参数方程、空间位置关系;历史背景、笛卡尔曲线在坐标面5.熟记特殊曲面的方程形式,上的投影的生平及笛卡尔判断给定方程解析几何的构思代表的曲面;过程,又要阐述其6.会求空间曲诞生的价值与意义.线在坐标面上的投影.(2)明确解析几
2 1.向量的概念; 2.相量 的线性 运算; 3.空间 直角坐 标系; 4.向量 线性运 算的坐标表示; 5.向量的模、方 向角、投影; 6.向量 的数量 积与向量积; 7.平面 及其方 程—曲 面方程 与空间 曲线方 程的概念、平面 的点法式方程、 平面的 一般方 程、两平面的夹 角; 9.空间 直线及 其方程 —间直 线的的 一般方 程、空间直线的 对称式 方程及 参数方程、两直 线的夹角、直线 与平面的夹角; 10.曲面及其方 程—曲 面研究 的基本问题、旋 转曲面、柱面、 二次曲面; 11.空间曲线及 其方程 —空间 曲线的 一般方 程、空间曲线的 参数方程、空间 曲线在 坐标面 上的投影. 1.正确理解向 量的概念,熟练 掌握向量加法 及数与向量乘 积的定义、运算 规律及其坐标 表示、熟记向量 的模、方向角的 计算公式,掌握 向量在轴上的 投影及其性质; 2.掌握向量积 和数量积的定 义和运算规律, 会用数量积和 向量积处理一 些几何问题; 3.熟练掌握平 面的一般方程、 点法式方程以 及截距式方程, 会求满足一定 条件的平面方 程,掌握点到平 面的距离公式, 会判断两平面 之间的位置关 系; 4.熟练掌握直 线的一般方程、 对称式和参数 方程,会求满足 一定条件的直 线方程,会判断 两直线及直线 与平面之间的 位置关系; 5.熟记特殊曲 面的方程形式, 判断给定方程 代表的曲面; 6.会求空间曲 线在坐标面上 的投影. 1.教学设计及教 学建议 (1)解析几何又 称为坐标几何或 笛卡儿几何,这是 数学发展史上的 一座重要的里程 碑.解析几何的创 立揭示了代数与 几何内在的联系, 为人们研究几何 问题或代数问题 提供了有效的研 究方法.解析几何 诞生的科学价值 体现在以下几个 方面: 1、开创了近现代 数学的先河; 2、提出了一切问 题都可以归结为 解方程问题的“通 用数学”方案,开 创了机械化的数 学计算方法; 3、提出了将数学 作为一种方法科 学的直观—演绎 法的方法论,使科 学方法论实现了 革命性的突破; 4、为微积分诞生 的创造了必要条 件. 因此在授课过程 中,既要穿插有关 解析几何产生的 历史背景、笛卡尔 的生平及笛卡尔 解析几何的构思 过程,又要阐述其 诞生的价值与意 义. (2)明确解析几 课程目标 1 课程目标 3 课程目标 5 课程目标 6 16
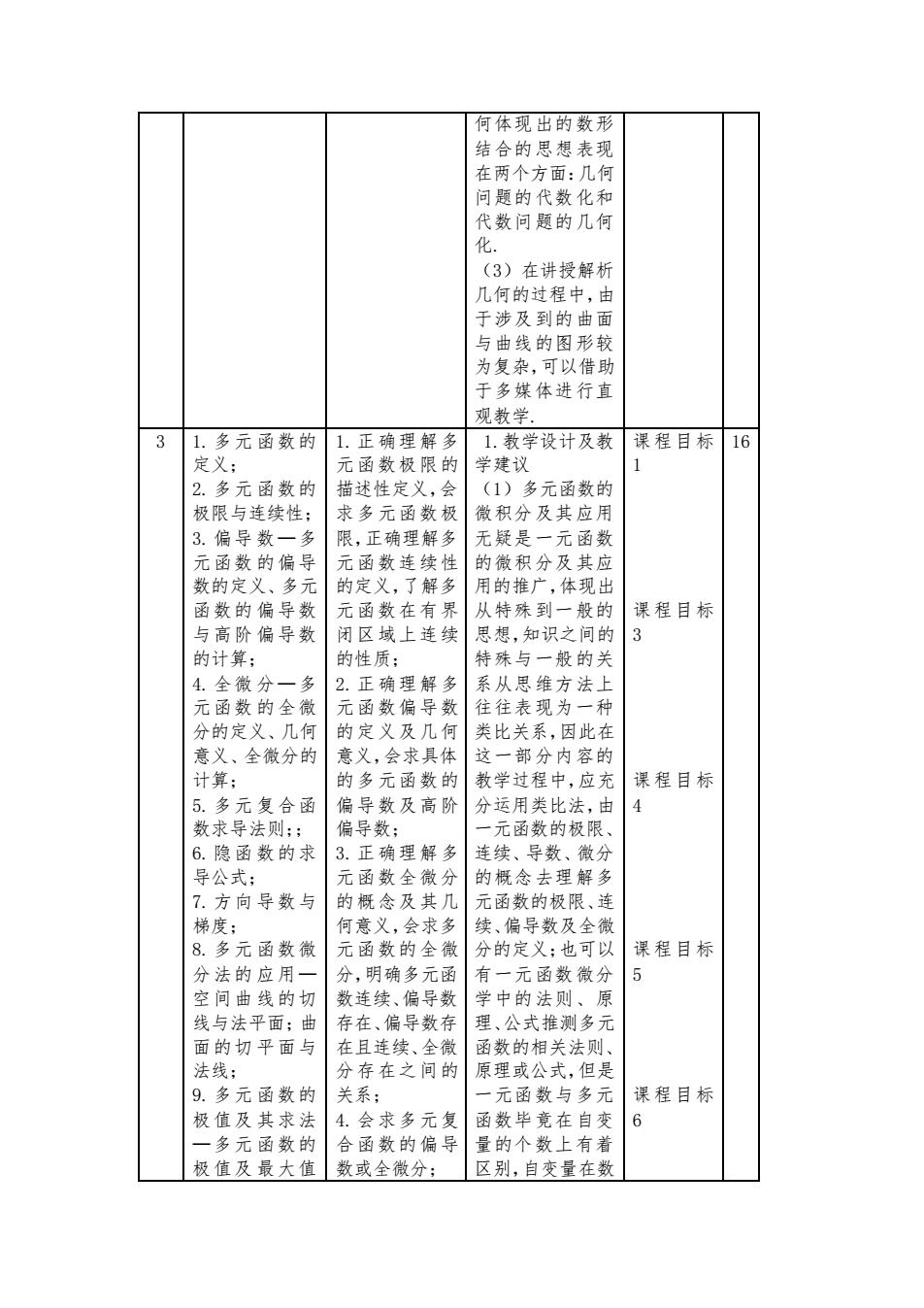
何体现出的数形结合的思想表现在两个方面:几何问题的代数化和代数问题的几何化.(3)在讲授解析几何的过程中,由于涉及到的曲面与曲线的图形较为复杂,可以借助于多媒体进行直观教学,1.多元函数的1.正确理解多1.教学设计及教课程目标|163定义;元函数极限的学建议12.多元函数的描述性定义,会(1)多元函数的极限与连续性;微积分及其应用求多元函数极3. 偏导数一多限,正确理解多无疑是一元函数元函数的偏导元函数连续性的微积分及其应数的定义、多元的定义,了解多用的推广,体现出元函数在有界从特殊到一般的函数的偏导数课程目标与高阶偏导数闭区域上连续思想,知识之间的3的计算;的性质;特殊与一般的关4.全微分一多2.正确理解多系从思维方法上元函数的全微元函数偏导数往往表现为一种分的定义、几何的定义及几何类比关系,因此在意义、全微分的意义,会求具体这一部分内容的计算;的多元函数的教学过程中,应充课程目标偏导数及高阶分运用类比法,由N5.多元复合函数求导法则;;偏导数;一元函数的极限、6.隐函数的求3.正确理解多连续、导数、微分导公式;元函数全微分的概念去理解多7.方向导数与的概念及其几元函数的极限、连梯度;何意义,会求多续、偏导数及全微元函数的全微课程目标8.多元函数微分的定义;也可以分法的应用一分,明确多元函5有一元函数微分空间曲线的切数连续、偏导数学中的法则、原存在、偏导数存理、公式推测多元线与法平面;曲面的切平面与在且连续、全微函数的相关法则、法线;分存在之间的原理或公式,但是9.多元函数的关系;一元函数与多元课程目标极值及其求法4.会求多元复函数毕竞在自变61一多元函数的合函数的偏导量的个数上有着极值及最大值区别,自变量在数数或全微分;
何体现出的数形 结合的思想表现 在两个方面:几何 问题的代数化和 代数问题的几何 化. (3)在讲授解析 几何的过程中,由 于涉及到的曲面 与曲线的图形较 为复杂,可以借助 于多媒体进行直 观教学. 3 1.多元 函数的 定义; 2.多元 函数的 极限与连续性; 3.偏导 数—多 元函数 的偏导 数的定义、多元 函数的 偏导数 与高阶 偏导数 的计算; 4.全微 分—多 元函数 的全微 分的定义、几何 意义、全微分的 计算; 5.多元 复合函 数求导法则;; 6.隐函 数的求 导公式; 7.方向 导数与 梯度; 8.多元 函数微 分法的 应用— 空间曲 线的切 线与法平面;曲 面的切 平面与 法线; 9.多元 函数的 极值及 其求法 —多元 函数的 极值及 最大值 1.正确理解多 元函数极限的 描述性定义,会 求多元函数极 限,正确理解多 元函数连续性 的定义,了解多 元函数在有界 闭区域上连续 的性质; 2.正确理解多 元函数偏导数 的定义及几何 意义,会求具体 的多元函数的 偏导数及高阶 偏导数; 3.正确理解多 元函数全微分 的概念及其几 何意义,会求多 元函数的全微 分,明确多元函 数连续、偏导数 存在、偏导数存 在且连续、全微 分存在之间的 关系; 4.会求多元复 合函数的偏导 数或全微分; 1.教学设计及教 学建议 (1)多元函数的 微积分及其应用 无疑是一元函数 的微积分及其应 用的推广,体现出 从特殊到一般的 思想,知识之间的 特殊与一般的关 系从思维方法上 往往表现为一种 类比关系,因此在 这一部分内容的 教学过程中,应充 分运用类比法,由 一元函数的极限、 连续、导数、微分 的概念去理解多 元函数的极限、连 续、偏导数及全微 分的定义;也可以 有一元函数微分 学中的法则、原 理、公式推测多元 函数的相关法则、 原理或公式,但是 一元函数与多元 函数毕竟在自变 量的个数上有着 区别,自变量在数 课程目标 1 课程目标 3 课程目标 4 课程目标 5 课程目标 6 16

与最小值、条件「5.利用隐函数量上的变化有时极值-拉格朗日会引起在性质上的求导公会求乘数法..由方程确定的的改变,正因如隐函数的导数此,在学习多元函数相关性质时,应或偏导数,简介方程组的情形;注意二者之间的区别,如连续与偏6.会求空间曲导数的关系、偏导线的切线与法平面的方程,会数与全微分的关系等.求曲面的切平(2)应注意化归面与法线的方程思想的运用。7.简介方向导多元函数极限的求法、偏导数与高数与梯度阶偏导数的计算7.熟练掌握多最终转化为一元元函数极值、最函数极限与一元大值与最小值函数导数相应的的求法,能够解方法与公式:在证决一些经济领明有关原理、公式域或工程技术或方法的过程中,领域的实际问注重把多元函数题的问题转化为一元函数的相应问题,如全微分存在的必要条件的证明、拉格朗日乘数法的推导都体现出化繁为简、化难为易、化不熟悉为熟悉的化归思想.1.教学设计及教1.二重积分的1.正确理解二课程目标18A概念与性质一1重积分的定义学建议二重积分的概和性质;(1)借助于类比法念、二重积分的2.熟练掌握运由曲边梯形面积性质;用直角坐标及的求法探讨曲顶2.二重积分计极坐标计算二柱体的体积的计课程目标3算法一利用直重积分的具体算方法,即分割、角坐标计算二步骤;近似、求和、取极重积分、利用极3.熟练解决直限,进而由定积分坐标计算二重角坐标系下的的定义类比叙述积分;两种不同积分出二重积分的定课程目标3.重积分的应次序的二次积义,再由定积分的4
与最小值、条件 极值-拉格朗日 乘数法. 5.利用隐函数 的求导公会求 由方程确定的 隐函数的导数 或偏导数,简介 方程组的情形; 6.会求空间曲 线的切线与法 平面的方程,会 求曲面的切平 面与法线的方 程 7.简介方向导 数与梯度 7.熟练掌握多 元函数极值、最 大值与最小值 的求法,能够解 决一些经济领 域或工程技术 领域的实际问 题 量上的变化有时 会引起在性质上 的改变,正因如 此,在学习多元函 数相关性质时,应 注意二者之间的 区别,如连续与偏 导数的关系、偏导 数与全微分的关 系等. (2)应注意化归 思想的运用. 多元函数极限的 求法、偏导数与高 阶偏导数的计算 最终转化为一元 函数极限与一元 函数导数相应的 方法与公式;在证 明有关原理、公式 或方法的过程中, 注重把多元函数 的问题转化为一 元函数的相应问 题,如全微分存在 的必要条件的证 明、拉格朗日乘数 法的推导都体现 出化繁为简、化难 为易、化不熟悉为 熟悉的化归思想. 4 1.二重 积分的 概念与 性质— 二重积 分的概 念、二重积分的 性质; 2.二重 积分计 算法— 利用直 角坐标 计算二 重积分、利用极 坐标计 算二重 积分; 3.重积 分的应 1.正确理解二 重积分的定义 和性质; 2.熟练掌握运 用直角坐标及 极坐标计算二 重积分的具体 步骤; 3.熟练解决直 角坐标系下的 两种不同积分 次序的二次积 1.教学设计及教 学建议 (1)借助于类比法 由曲边梯形面积 的求法探讨曲顶 柱体的体积的计 算方法,即分割、 近似、求和、取极 限,进而由定积分 的定义类比叙述 出二重积分的定 义,再由定积分的 课程目标 1 课程目标 3 课程目标 4 18