《线性代数》课程教学课件（PPT讲稿，A）§3.4 分块矩阵

线性代数 第三章第三车$ 3.4分块矩阵一、分块矩阵的概念二、分块矩阵的运算三、分块对角矩阵

线性代数 第三章 一、分块矩阵的概念 二、分块矩阵的运算 三、分块对角矩阵 §3.4 分块矩阵

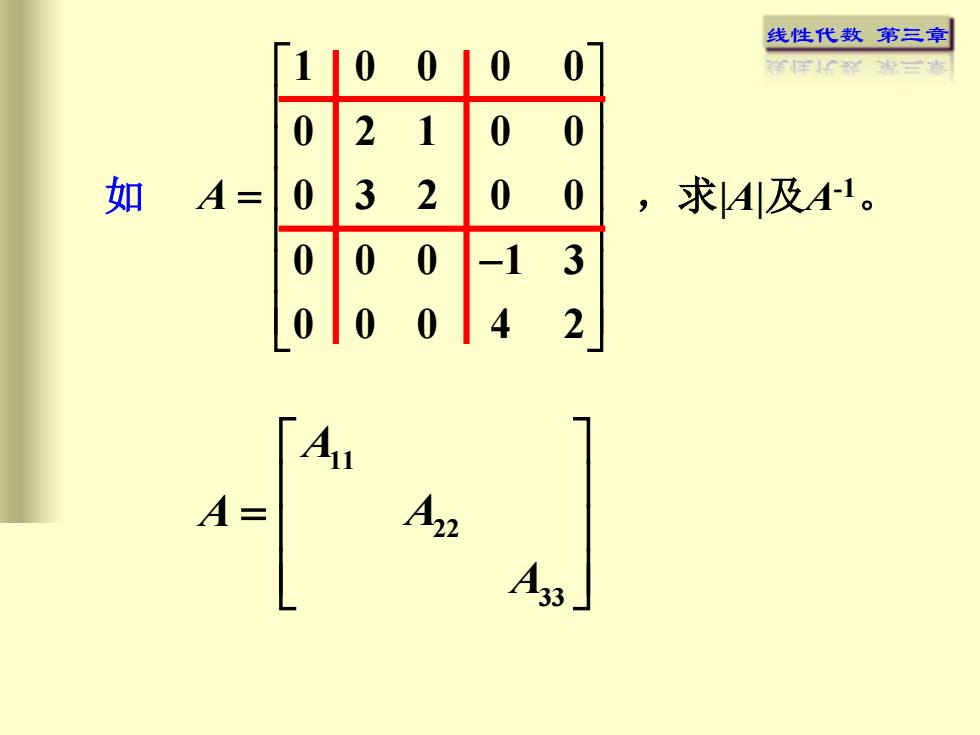
线性代数第三章00001祥样三草0200130020如A=，求[A|及A-1。0030-100204AlA=V22A33

线性代数 第三章 如 11 22 33 A A A A     =       1 0 0 0 0 0 2 1 0 0 0 3 2 0 0 0 0 0 1 3 0 0 0 4 2 A       =     −       ，求|A|及A-1

线性代数第三章花三一、分块矩阵的概念定义设A是一个矩阵，在A的行或列之间加上一些线，把这个矩阵分成若干小块：用这种方法被分成若干小块的矩阵叫做一个分块矩阵.每一小块称为A的子块，每一个分块的方法叫做A一种分法ala12a13ay115则A可记作a22123aa2)2524例如 A=AA2A3A=(13)a32a34a33135A23AA22A54a42a43a44

线性代数 第三章 一、分块矩阵的概念 定义 设A是一个矩阵，在A的行或列之间加上一些 线，把这个矩阵分成若干小块．用这种方法被分成 若干小块的矩阵叫做一个分块矩阵.每一小块称为A 的子块，每一个分块的方法叫做A一种分法. 例如 31 32 3 11 3 13 14 23 24 1 41 42 5 25 34 43 4 12 2 35 1 4 5 22 4 a a a a a a a a a a a a a a a a a a a A a       =       则A可记作 21 1 12 3 1 2 2 13 A 2 A A A A A   A =    

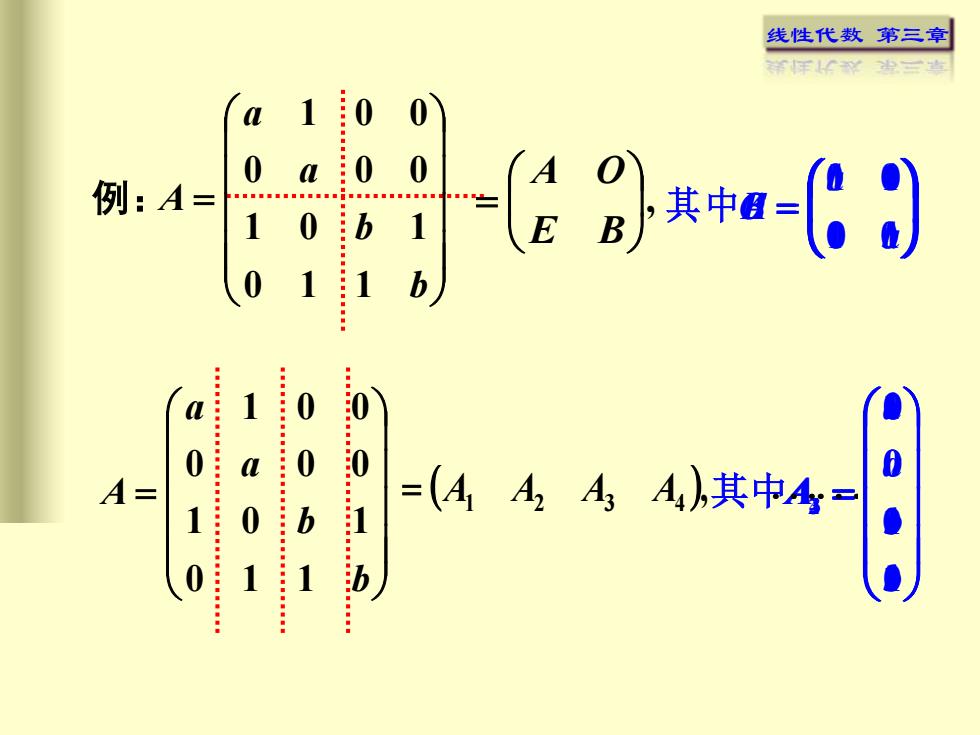
线性代数第三章祥彩光三草000A1例: A=其中=BEb一1a0i0=(A A, A, A),其中A=A=b0b

线性代数 第三章 ,  = E B A O ( ), = A1 A2 A3 A4   = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0   = b b a a A 0 1 1 1 0 1 0 0 0 1 0 0   = a a A 0 1 其 中   = b b B 1 1   = 0 1 1 0 E   = 0 0 0 0 O   = 010 1 a 其中 A   = 101 2 a A   = 100 3 b A   = b A 100 4 例：

线性代数第三章祥样三草323248856567而：-3-2-3-1-1-24-4-6?-8-7-7-6?不是分块矩阵

线性代数 第三章 1 2 3 4 5 6 7 8 4 3 2 1 8 7 6 5         − − − −     − − − − 1 2 3 4 5 6 7 8 4 3 2 1 8 7 6 5         − − − −     − − − − 而： 不是分块矩阵