
线性代数 第五章例如x+xx,+3xX+2x+4x,x,+3xixx, +5x +(3+i)x,x, + /2x)x都为二次型:我们下面讨论的二次型均为实二次型设由y1,J2..,y,到变量xi,2...,x,的线性变换为X, =Ciiyi +Ci2J2 +... +CinyngX, =C21Ji +C22y2 +...+C2nJ'n(5 -12)X, =CniJi +Cn2J'2 +...+CnnJ'n
线性代数 第五章 例如 都为二次型;我们下面讨论的二次型均为实二次型. 2 2 2 1 1 2 1 3 2 2 3 3 2 1 2 2 2 3 1 4 3 2 4 3 5 (3 ) 2 x x x x x x x x x ix x x i x x x x + + + + + + + + + 1 2 1 2 1 11 1 12 2 1 2 21 1 22 2 2 1 1 2 2 , , , , , , , , (5 12) . n n n n n n n n n nn n y y y x x x x c y c y c y x c y c y c y x c y c y c y = + ++ = + ++ − = + ++ 设由 到变量 的线性变换为

线性代数第五或写成为矩阵形式:X=CYX1X2y2其中X=VC = (Cj,)mxn可见,乡线性变换把二次型变为二次型
线性代数 第五章 或写成为矩阵形式: X CY = 1 1 2 2 , ( )ij m n n n x y x y X Y C c x y = = = 其中 , 可见,线性变换把二次型变为二次型

线性代数 第五章二、二次型的矩阵表示取a;=aij"则2a;x,x, =ajx,x, +anx,x,(i<j)于是f =aux +axx, +...+ainxxn+a2xx +a2x +...+a2nxxn+·.+anxnX,+anxX,+...+amx?X(auX +ax, +..+anxn)+x2(a21xX+a22x, +... +a2nxn)+:+X,anX,+anX +...+annxn
线性代数 第五章 二、二次型的矩阵表示 2 11 1 12 1 2 1 1 2 21 2 1 22 2 2 2 2 1 1 2 2 n n n n n n n n nn n f a x a x x a x x a x x a x a x x a x x a x x a x = + + + + + + + + + + + + 1 1 11 12 2 1 2 21 1 22 2 2 1 1 2 2 ( ) ( ) ( ) n n n n n n n nn n a a x a x a x a x a x a x x x x a x x a x = + + + + + + + + + + + + 2 ( ) ji ij ij i j ij i j ji j i 取a a a x x a x x a x x i j = = + ,则 于是

线性代数 第五章aX, +aiX, +...+ainx,a2iX, +a22X, +...+a2nXn=[xi,X2,..,xn]aniXi+anX+..+annx,nnntanla2ain专121422a2n=[xi,x2,".,xn]xaahjn21nn
线性代数 第五章 11 12 1 1 21 22 2 2 1 2 1 2 [ , , , ] n n n n n nn n a a a x a a a x x x x a a a x = 11 1 12 2 1 21 1 22 2 2 1 2 1 1 2 2 [ , , , ] n n n n n n n nn n a x a x a x a x a x a x x x x a x a x a x + + + + + + = + + +
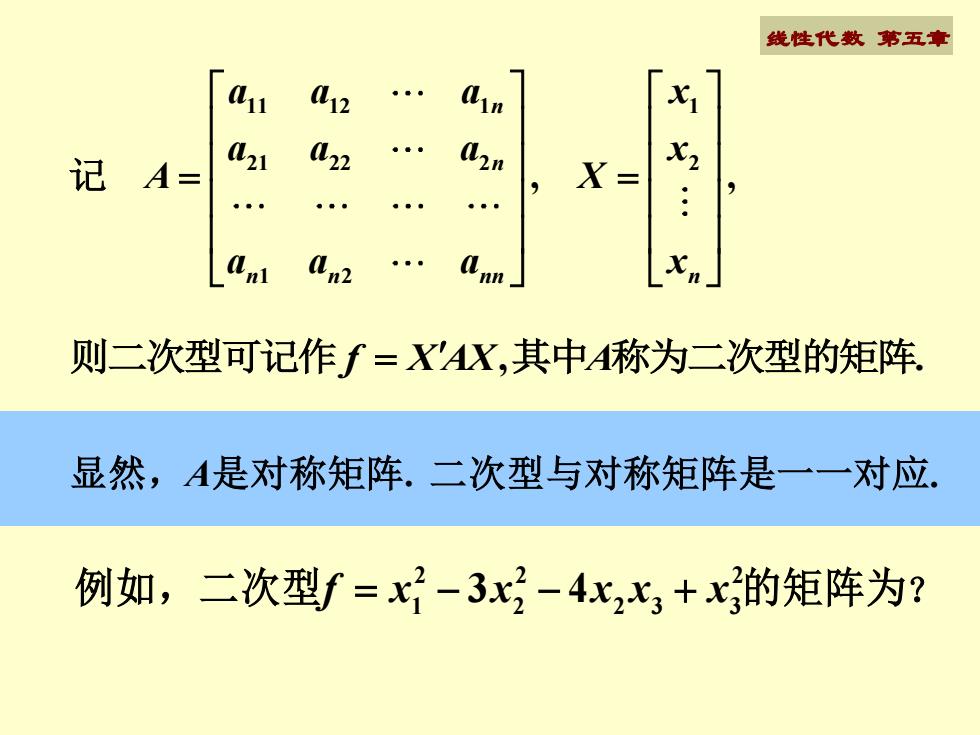
线性代数第五车anxia12ainX2a2122a2n记 A=X =aaanln2nn则二次型可记作f=XAX,其中A称为二次型的矩阵显然,A是对称矩阵.二次型与对称矩阵是一一对应例如,二次型f=x-3x2-4x,x+x的矩阵为?
线性代数 第五章 11 12 1 1 21 22 2 2 1 2 , , n n n n nn n a a a x a a a x A X a a a x = = 记 则二次型可记作 , . f X AX A = 其中 称为二次型的矩阵 显然,A是对称矩阵. 二次型与对称矩阵是一一对应. 2 2 2 1 2 2 3 3 例如,二次型f x x x x x = − − + 3 4 的矩阵为 ?