
第五章第一节定积分的概念及性质实际问题二、定积分的定义三、定积分的性质HIGH EDUCATION PRESS机动目录上页下页返回结束
第一节 一、实际问题 二、 定积分的定义 三、 定积分的性质 机动 目录 上页 下页 返回 结束 定积分的概念及性质 第五章
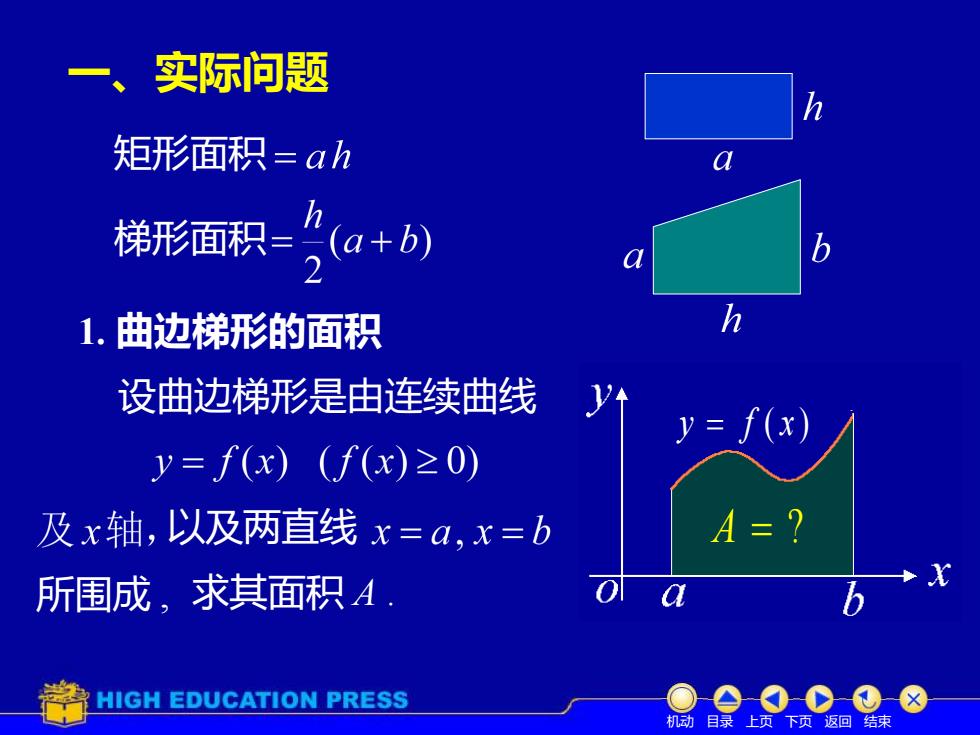
一、实际问题n矩形面积=aαh梯形面积=(a+b)bh1.曲边梯形的面积设曲边梯形是由连续曲线Vy= f(x)y=f(x) (f(x)≥0)A=?及x轴,以及两直线x=a,x=b0所围成,求其面积AaHIGH EDUCATION PRESS机动目录上页下页返回结束
一、实际问题 1. 曲边梯形的面积 设曲边梯形是由连续曲线 以及两直线 所围成 , 求其面积 A . A = ? 机动 目录 上页 下页 返回 结束 y = f ( x ) 矩形面积 梯形面积
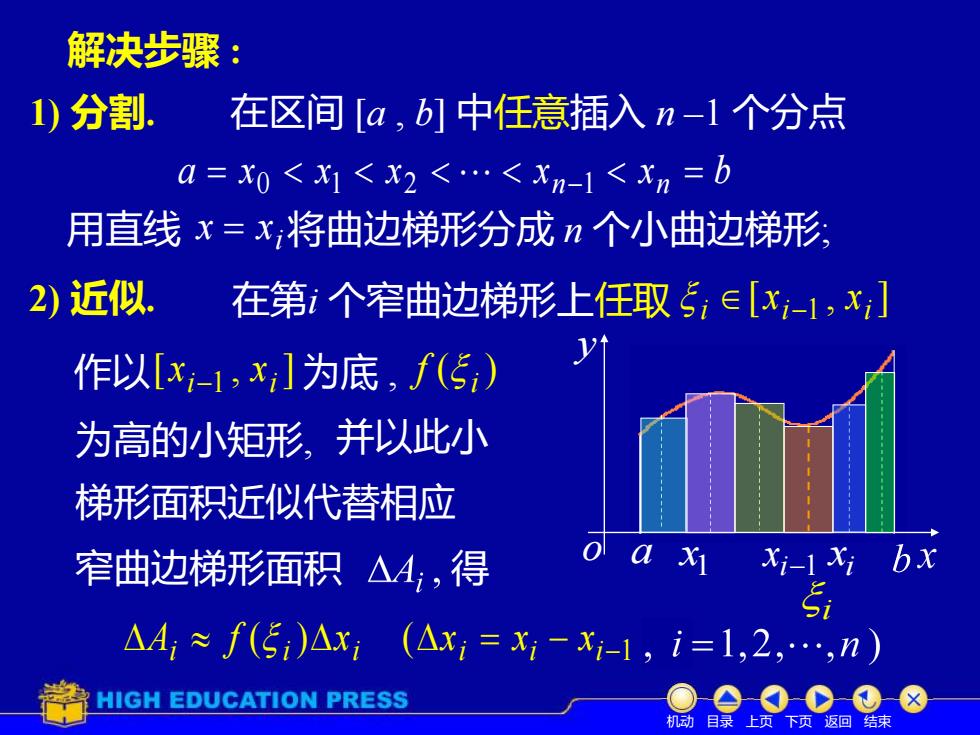
解决步骤:1) 分割在区间[α,b]中任意插入n-1个分点α= Xo < Xi < X2 <...<Xn-1 < Xn = b用直线x=x,将曲边梯形分成n个小曲边梯形2)近似在第i个窄曲边梯形上任取SiE[xi-1,xi]yt作以[xi-1,x,]为底,f(5)并以此小为高的小矩形梯形面积近似代替相应Qla xibxXi-1 Xi△Ai,得窄曲边梯形面积5iAA, = f(E)△xi(△xi = xi -xi-1 , i=1,2,.,nHIGH EDUCATION PRESS机动目录上页下页返回结束
1 x i x i−1 a x y o 解决步骤 : 1) 分割. 在区间 [a , b] 中任意插入 n –1 个分点 a x x x x x b = 0 1 2 n−1 n = [ , ] i i 1 i x x − 用直线 i x = x 将曲边梯形分成 n 个小曲边梯形; 2) 近似. 在第i 个窄曲边梯形上任取 作以 [ , ] i 1 i x x − 为底 , ( )i f 为高的小矩形, 并以此小 梯形面积近似代替相应 窄曲边梯形面积 得 ( ) ( ) i i i i = i − i−1 A f x x x x i 机动 目录 上页 下页 返回 结束
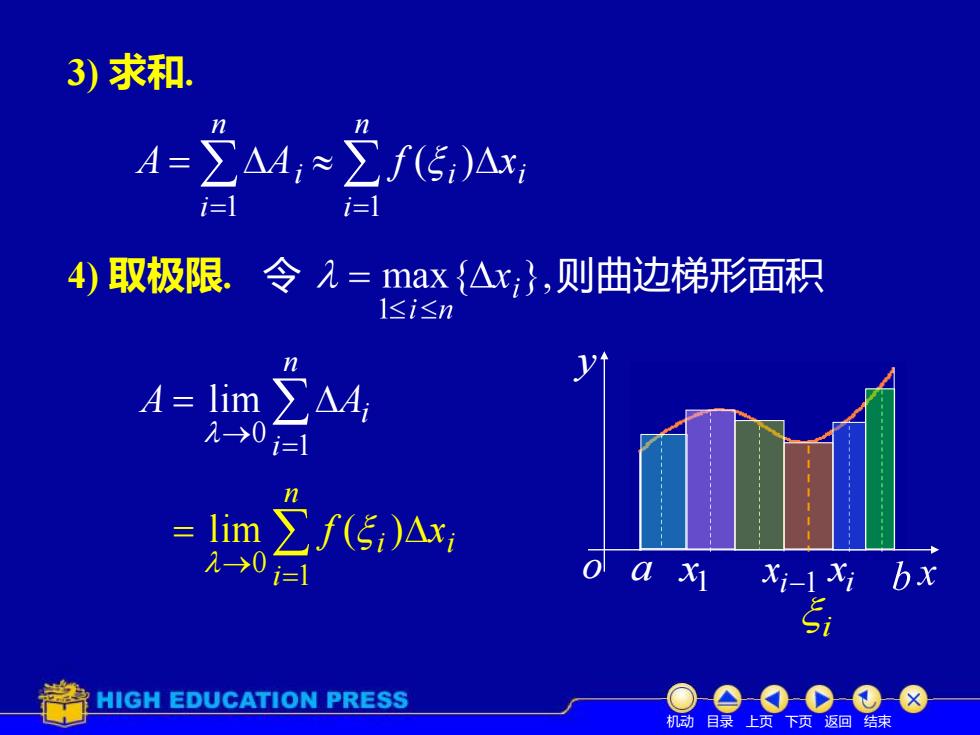
3)求和nYA=ZA; ~ Zf(5)Axii=1i=14)取极限令 =max{△x;,则曲边梯形面积<i<nnZA= limA;20i=1nZ.limf(Ei)Axi10i-1O1axibxXi-1 XiEHIGH EDUCATION PRESS机动目录上页下页返回结束
3) 求和. = = n i A Ai 1 = n i i i f x 1 ( ) 4) 取极限. 令 则曲边梯形面积 → = = n i A Ai 1 0 lim → = = n i i i f x 1 0 lim ( ) 机动 目录 上页 下页 返回 结束 a y o 1 x i x i−1 x i

2.变速直线运动的路程设某物体作直线运动已知速度 v=v(t) eC[T, T2], 且v(t)≥0,求在运动时间内物体所经过的路程 s.解决步骤:1) 分割在[Ti,T2]中任意插入 n-1个分点,将它分成n 个小段[ti-1,t;](i=1,2,,n),在每个小段上物体经过的路程为 △si(i=l,2,.., n)2)近似任取弓;ε[ti-1,ti],以v(s;)代替变速,得△ s, = v(S)At;(i=1,2,..,nHIGH EDUCATIONPRESS机动目录上页下页返回结束
2. 变速直线运动的路程 设某物体作直线运动, 且 求在运动时间内物体所经过的路程 s. 解决步骤: 1) 分割. 将它分成 在每个小段上物体经 2) 近似. 得 i i i s v( )t (i = 1, 2, , n) 已知速度 机动 目录 上页 下页 返回 结束 n 个小段 过的路程为