
复变函数如果,f(z)在C内有l个级数分别为ni,n2,",ni的零点a,a2",a,和m个级数分别为P1,P2,""Pm的极点bi,b2,"",bm2由以上所述和留数定理,得mf'(2)(2)1(?)dz=Res.0+2元17)Resbk,akf(z)f(z)k=-1k-lf'(z)dz =(n + n2 +...+ n) -(P + P2 +...+ Pm)2元if(z)(f(z)或dz=N-P[证毕]2元 i f(z)山
6 , , , , , , , , , , ( ) , , , 1 2 1 2 1 2 1 2 m l m l b b b a a a m p p p f z C l n n n 的极点 的零点 和 个级数分别为 如果 在 内有 个级数分别为 = C z f z f z i d ( ) ( ) 2π 1 , , ( ) ( ) , Res ( ) ( ) Res 1 1 = = + m k k l k k b f z f z a f z f z d ( ) ( ) ( ) 2π 1 1 2 l C z n n n f z f z i = + + + ( ), − p1 + p2 ++ pm d . ( ) ( ) 2π 1 z N P f z f z i C = − 或 [证毕] 由以上所述和留数定理,得
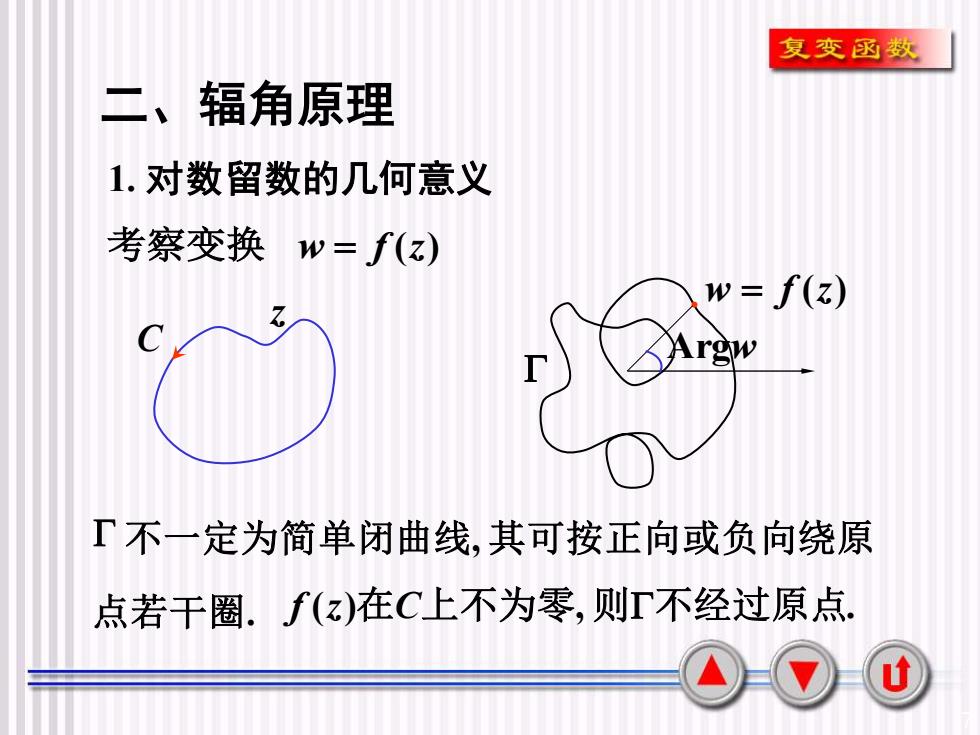
复变函数二、辐角原理1.对数留数的几何意义考察变换 w=f(z)w = f(z)rgw不一定为简单闭曲线,其可按正向或负向绕原点若干圈.f(z)在C上不为零,则I不经过原点u
7 二、辐角原理 考察变换 w = f (z) C z .w = f (z) Argw 不一定为简单闭曲线, 其可按正向或负向绕原 点若干圈. f (z)在C上不为零, 则不经过原点. 1. 对数留数的几何意义
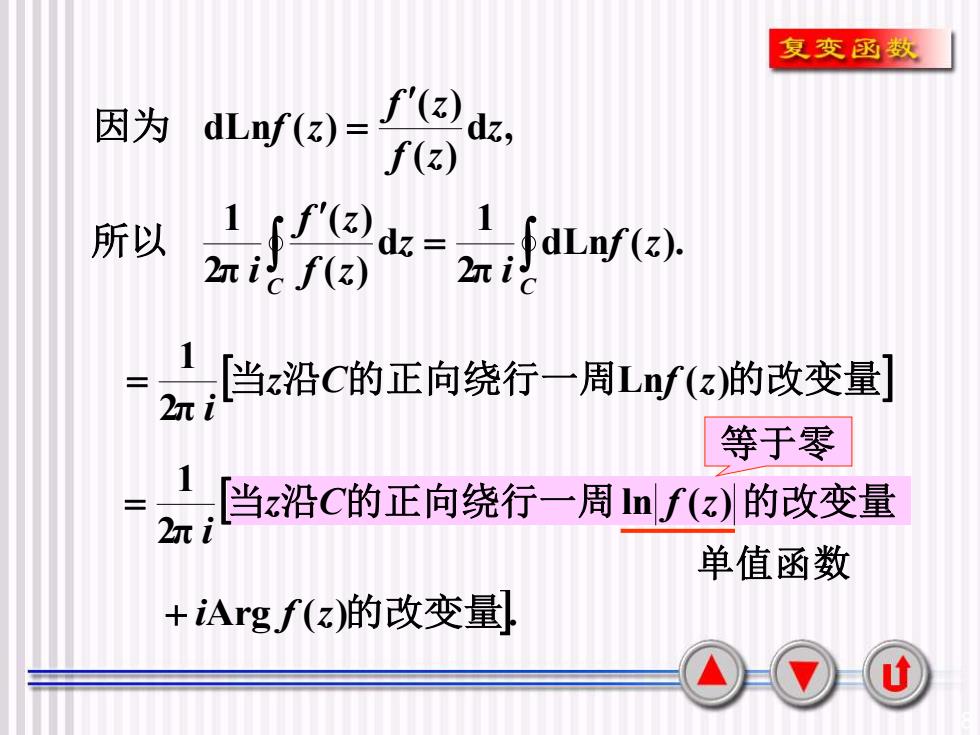
复变函数f'(z)因为dz,dLnf(z)-f(z)4所以dLnf(z)dz.三2元 i (z)2元 i当z沿C的正向绕行一周Lnf(z)的改变量2元等于零当z沿C的正向绕行一周Inlf(z)的改变量2元单值函数+iArg.f(z)的改变量u
8 d , ( ) ( ) dLn ( ) z f z f z f z 因为 = dLn ( ). 2π 1 d ( ) ( ) 2π 1 = C C f z i z f z f z i 所以 当 沿 的正向绕行一周Ln ( )的改变量 2π 1 z C f z i = 当 沿 的正向绕行一周ln ( ) 的改变量 2π 1 z C f z i = + iArg f (z)的改变量. 单值函数 等于零