第八节多元函数的极值及其求法函数z=3sin x+3sin y+3sin(x+y)的图形如下,可以看出该函数有无穷多个极小值和极大值7XMathGS上页下页返回公式数学家线与面
第八节 多元函数的极值及其求法 函数 z = 3sin x + 3sin y + 3sin( x + y) 的图形如下, 该函数有无穷多个极小值和极大值. 可以看出 x y z

第八节多元函数的极值及其求法函数x2+y2-z2=-1 的图形如下,可以看出该函数的极Z小值大于极大值xMathGS上页下页返回公式数学家线与面
第八节 多元函数的极值及其求法 x y z O 函数 1 2 2 2 x + y − z = − 的图形如下, 小值大于极大值. 可以看出该函数的极

第八节多元函数的极值及其求法2.二元函数极值存在的条件定理1(必要条件)函数z=f(x,y)在点(xo,yo)存在偏导数,且在该点取得极值,则有f(xo, yo)=0, f,(xo, yo)=0证明台使两个偏导数都为0的点称为函数的驻点.定理1说明,可微函数的极值一定在驻点处取得,但驻点不一定都是极值点.例如,z=xy在驻点(0,0)处不取极值MathGS数学家上页下页返回公式线与面
第八节 多元函数的极值及其求法 2. 二元函数极值存在的条件 定理1 (必要条件) 函数 z = f (x , y) 在点 (x0 , y0 ) 存 在偏导数, ( , ) 0 , ( , ) 0 . f x x0 y0 = f y x0 y0 = 且在该点取得极值 , 则有 第八节 多元函数的极值及其求法 在偏导数, 证明 定理1 (必要条件) 函数 z = f (x , y) 在点 (x0 , y0 ) 存 ( , ) 0 , ( , ) 0 . f x x0 y0 = f y x0 y0 = 且在该点取得极值 , 则有 不妨设 z = f (x , y) 在点 (x0 , y0 )处有极大值. 则由极大值的定义,在点 (x0 , y0 )的某个邻域内恒有 f (x , y) < f (x0 , y0 ), ((x , y) (x0 , y0 )). 于是,当 y = y0时,有 f (x , y0 ) < f (x0 , y0 ), (x x0 ). 这说明一元函数z = f (x , y0 ) 在 x = x0 处取得极大值, 使两个偏导数都为 0 的点称为函数的驻点. 都是极值点. 明,可微函数的极值一定在驻点处取得, 例如,z =xy 在驻点( 0, 0 )处不取极值. 定理1说 但驻点不一定

第八节多元函数的极值及其求法定理2(充分条件)若函数z=f(x,y)在点(xo,yo)的某邻域内具有一阶和二阶连续偏导数,且fi(xo, yo)=0, f,(xo, yo) = 0,令A= fxr(xo,yo), B= fx,(xo,yo), C= fy,(xo,yo)A<0时取极大值,则1)当 AC-B2>0时,具有极值A>0时取极小值:2)当AC-B2<0 时,没有极值;3)当AC -B2 =0 时,不能确定,需另行讨论,证明见第九节.只举例说明当AC-B2=0的情形MathGS上页下页返回公式线与面数学家
第八节 多元函数的极值及其求法 时, 具有极值 的某邻域内具有一阶和二阶连续偏导数, 令 则 1) 当 A<0 时取极大值, A>0 时取极小值; 2) 当 3) 当 证明见第九节. 时, 没有极值; 时, 不能确定, 需另行讨论. ( , ) 0 , ( , ) 0 , f x x0 y0 = f y x0 y0 = ( , ) , ( , ) , ( , ) , 0 0 0 0 0 0 A f x y B f x y C f x y = x x = x y = y y 0 2 AC − B 0 2 AC − B 0 2 AC − B = 且 若函数 z = f (x , y) 在点 (x0 , y0 定理2 (充分条件) ) 只举例说明当 AC – B2 = 0 的情形
第八节多元函数的极值及其求法考察函数 f(x,)=x2+y4 和 g(x,)=x2+容易验证,这两个函数都以(0,0)为驻点,且在点(0,0)处都满足AC-B2=0. 但f(x,J)在(0,0)处有极小值而g(x,J)在(0,0)处却没有极值Z/(x,y)=x+J4Zxy(x,)=x+yxMathGS公式上页下页返回线与面数学家
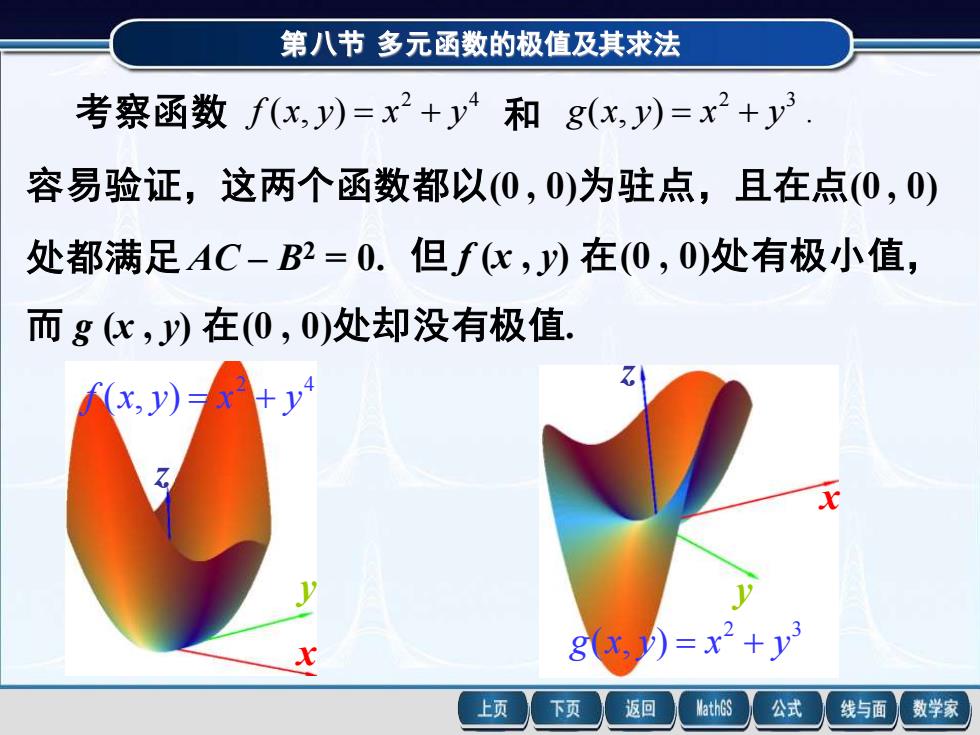
第八节 多元函数的极值及其求法 考察函数 2 4 f (x, y) = x + y 和 ( , ) . 2 3 g x y = x + y 容易验证,这两个函数都以(0 , 0)为驻点,且在点(0 , 0) 处都满足 AC – B2 = 0. 但 f (x , y) 在(0 , 0)处有极小值, 而 g (x , y) 在(0 , 0)处却没有极值. 2 4 f (x, y) = x + y x y z 2 3 g(x, y) = x + y x y z