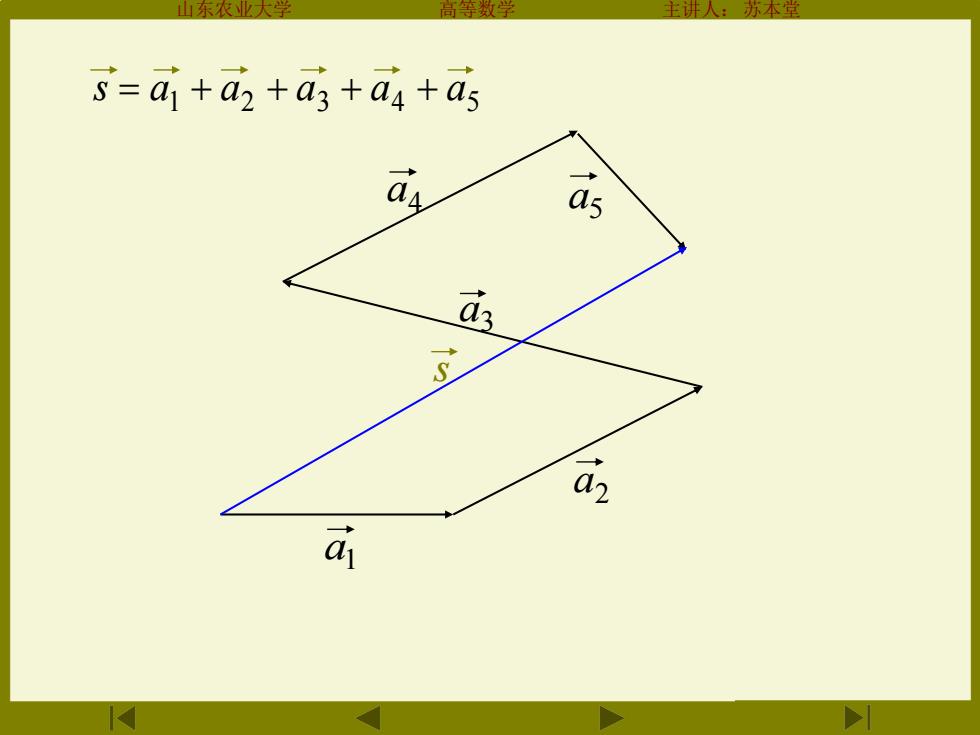
1东农大 等数雪 主讲人:苏本堂 =☑1+a2+a3+a4+a5 g 4 a a
山东农业大学 高等数学 主讲人:苏本堂 s a3 a4 a5 a2 a1 1 2 3 4 5 s = a + a + a + a + a

2.向量的减法 6-d=b+(-a -a -à b-a 特别当b=a时,有 a-a-a+(-a)-0 a 三角不等式 a+b≤a+b a-b≤a+b P DI
山东农业大学 高等数学 主讲人:苏本堂 2. 向量的减法 三角不等式 a

1-/ 3.向量与数的乘法 入是一个数,入与a的乘积是一个新向量,记作2d. 规定:>0时,a与ā同向,a=2d; <0时,a与a反向,a=-a; =0时,a=0. 总之: aa=n a 运算律:结合律(ud)=u(2d)=ud 分配律(+)a=九a+ud 2(a+b)=元a+2b 若#0,则有单位向量a=日a 因此a=aa
山东农业大学 高等数学 主讲人:苏本堂 a a = 3. 向量与数的乘法 是一个数 , a . 规定 : 1a a ; = 可见 1a a ; − = − 与 a 的乘积是一个新向量, 记作 总之: 运算律 : 结合律 ( a) ( a) = a = 分配律 (a b) + a b = + = 则有单位向量 a . 1 a a 因此 a = a a

定理1.设a为非零向量,则 allb 三方=人a(八为唯一实数) 直线上点的坐标 点P一向量OP=xi·一实数x 轴上点P的坐标为x的充分必要条件是OP=xi 平面上点的坐标 点M一向量OM=OP+PM =0P+00=xi+yj=(x,y) M 轴上点M的坐标为(x,y)的充分 必要条件是OM=xi+yj
山东农业大学 高等数学 主讲人:苏本堂 定理1. 设 a 为非零向量 , 则 ( 为唯一实数) a∥b . . O i P x 点P OP = xi 实数x x 轴上点P的坐标为x的充分必要条件是 OP = xi 直线上点的坐标 平面上点的坐标 O Q p M x y i j 点M 向量 OM OP PM = + = + OP OQ = + x i y j = ( , ) x y 轴上点M的坐标为(x,y)的充分 必要条件是 OM = + x i y j 向量

办本堂 三、空间直角坐标系 1.空间直角坐标系的基本概念 过空间一定点0,由三条互相垂直的数轴按右手规则 组成一个空间直角坐标系 zz轴(竖轴) ·坐标原点 m ·坐标轴 y0z面 ·坐标面 0x面 +V 卦限(八个) 0x0面 轴(纵轴) x轴(横轴)
山东农业大学 高等数学 主讲人:苏本堂 Ⅶ Ⅱ Ⅲ Ⅵ x y z Ⅴ Ⅷ Ⅳ 三、空间直角坐标系 由三条互相垂直的数轴按右手规则 组成一个空间直角坐标系. • 坐标原点 • 坐标轴 x轴(横轴) y轴(纵轴) z 轴(竖轴) 过空间一定点o , o • 坐标面 • 卦限(八个) xoy面 yoz面 1. 空间直角坐标系的基本概念 Ⅰ