
集合的概念 第一章函数、连续与极限 我们把自然数的全体组成的集合称为自然数集,记作N.由整数的全体 构成的集合称为整数集,记为Z.用Q表示全体有理数构成的有理数集,R 表示全体实数构成的实数集,显然有NcZcQcR 如果是正整数集,则记为Z+,负整数集记为Z-,以此类推 注:在本书中所讨论的数集除特别说明外均为实数集
6 一、 集合的概念 第一章 函数、连续与极限 我们把自然数的全体组成的集合称为自然数集,记作 . 由整数的全体 构成的集合称为整数集,记为 . Q R Z Q R 用 表示全体有理数构成的有理数集, 表示全体实数构成的实数集. 显然有 . 如果是正整数集,则记为 𝑍 + ,负整数集记为 𝑍 −,以此类推. 注: 在本书中所讨论的数集除特别说明外均为实数集
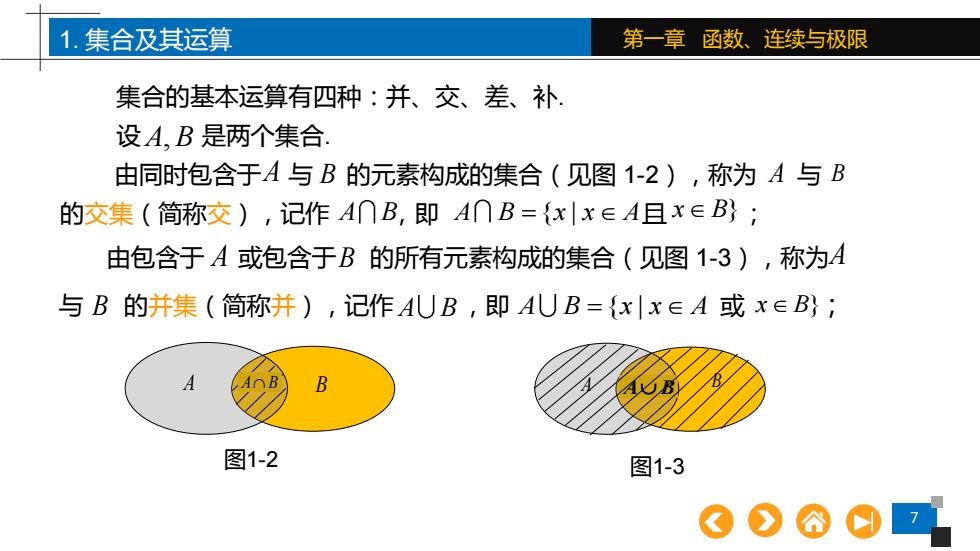
1.集合及其运算 第一章函数、连续与极限 集合的基本运算有四种:并、交、差、补 设A,B是两个集合 由同时包含于A与B的元素构成的集合(见图1-2),称为A与B 的交集(简称交),记作A∩B,即A∩B={x|x∈A且x∈B}; 由包含于A或包含于B的所有元素构成的集合(见图1-3),称为A 与B的并集(简称并),记作AUB,即AUB={x|x∈A或x∈B}; B 图1-2 图1-3
7 1. 集合及其运算 第一章 函数、连续与极限 由同时包含于 与 的元素构成的集合(见图 1-2),称为 与 的交集(简称交),记作 ,即 且 ; A B A B A B x x A = { | x B } A B 由包含于 或包含于 的所有元素构成的集合(见图 1-3),称为 与 的并集(简称并),记作 A B ,即 A B x x A = { | 或 x B } ; A B A B 集合的基本运算有四种:并、交、差、补. 设 A B, 是两个集合. A A B B 图1-2 A A B B 图1-3

1.集合及其运算 第一章函数、连续与极限 由包含于A但不包含于B的元素构成的集合(见图1-4),称为A与 B的差集(简称差),记作A\B,即A\B={x|x∈A且xEB}; 特别地,若我们所讨论的问题在某个集合(称为基本集或全集,一般记为 U)中进行,集合A是U的子集(见图1-5),此时称U八A为A的余集 (或补集),记作CuA或AC A或CuA B A\B U 图1-4 图1-5
8 1. 集合及其运算 第一章 函数、连续与极限 由包含于 但不包含于 的元素构成的集合(见图 1-4),称为 与 的差集(简称差),记作 ,即 且 ; A B A B A B\ A B x x A \ { | = x B } 特别地,若我们所讨论的问题在某个集合(称为基本集或全集,一般记为 U )中进行, A U c A C A 或 U A B 图1- 4 图1-5 A B\ 集合 A 是 U 的子集 (见图 1-5),此时称 为 的余集 (或补集),记作 或 . U A\ C AU C A A

1.集合及其运算 第一章函数、连续与极限 关于集合的余集,我们有如下性质 性质1(对偶性质)设U是一个基本集,A,B是它的两个子集,则 01 (AUB)=A∩B9 02 (A∩B)=AUBO
9 1. 集合及其运算 第一章 函数、连续与极限 关于集合的余集,我们有如下性质. 性质1(对偶性质) 设 U 是一个基本集, A B, 是它的两个子集,则 ( ) C C C A B A B = ( ) C C C A B A B = 01 OPTION 02 OPTION

1.集合及其运算 第一章函数、连续与极限 除了集合的四种基本运算,我们还可以定义两个集合的乘积 设A,B是两个非空的集合,则由有序数对(x,y)组成的集合 A×B={(x,y)川x∈A,y∈B} 2 AxB 称为A与B的直积 B=0,2) 例如: 设A=[0,1],B=[0,2] 则A×B={(x,y)川0≤x≤1,0≤y≤2},如图1-6所示 R×R={(x,y)川x,y∈R}即为xOy面上全体点 0A=0,1山1 的集合,R×R常记作R2. 图1-6 10
10 1. 集合及其运算 第一章 函数、连续与极限 1 2 x y O A = [0,1] B = [0, 2] A B 设 A B, 是两个非空的集合,则由有序数对 ( x y, ) 组成的集合 称为 与 的直积. 例如: A B x y x A y B = {( , ) | , } A B 设 A B = = [0,1], [0,2] 即为 面上全体点 的集合, 常记作 . R R {( , ) | , R} = x y x y xOy R R 2 R 图1-6 则 A B x y x y = {( , ) | 0 1, 0 2} ,如图 1-6所示. 除了集合的四种基本运算,我们还可以定义两个集合的乘积