
2019-2020山东理工大学《高等数学CI》答案 填空题(每空2分,共30分) 1x>2 2、e 3 4.1 2 、ef'x) 7、x=-1 8、e 9、0 10、(1,0) 11 1 12、y=1 3、B 14、D 15、B 计算题(每题6分,共48分) 、 2卿e-sn 1-cosx 3x2+2x-5 x =卿3x8+53 223 =lim =-15 =25 4、y=2 x arctan.x-+1.3 3 广-2 arctanx+5n5 1x2 -lim 2x 5 =0 程两边同时对x求导数 y+y=e*"(1+y3 t y=ew-y x-exty .5 . 列 5 =∫darctanx.3 +C5 9、令压=,则=式,=h2 a 4 =2-ln(1+V2).5 共2页第1页
2019-2020 山东理工大学《高等数学 CI》答案 一、 填空题(每空 2 分,共 30 分) 1、 x 2 2、 e 3、3 4、1 5、2 6、 ( ) ( ) f x e f x dx 7、 x =−1 8、 2 x xe− 9、0 10、(1,0) 11、 1 12、 y = 1 13、 B 14、D 15、B 二、计算题(每题 6 分,共 48 分) 1、 3 2 3 2 0 5 lim x 4 5 x x x → x x x + − − + 2、 0 ( 1)sin lim 1 cos x x e x → x − − 2 2 0 3 2 5 lim x 3 8 5 x x → x x + − = − + .3 2 2 lim 1 2 x x x → = .3 = −1 .5 = 2.5 3、 0 1 1 lim x→ sin x x − 4、 y x x = + 2 arctan 1 .3 0 sin lim x sin x x → x x − = .3 2 2 2arctan 1 x y x x = + + . 5 0 2 0 1 cos lim 2 1 2 lim 2 0 x x x x x x → → − = = = .5 5、程两边同时对 x 求导数 6、 2 2 2 1 dy dy t dt t dx dx dt t = = = (1 ) x y y xy e y + + = + .3 2 2 2 4 4 1 d y t t dx t = = .4 x y x y e y y x e + + − = − .5 2 2 1 4 t d y dx = = .5 arctan 2 1 7 1 x e dx + x 、 8、 1 1 x dx + e (1 ) x x x de e e = + ln 1 x x e C e = + + .5 arctan arctan x = e d x .3 arctan x = + e C .5 9、令 1 2 2 , , 2 x t x t dx tdt = = = 则 .2 1 0 1 1 2 dx + x = 2 0 1 t dt + t .4 = 2 ln(1 2) − + .5 共 2 页 第 1 页
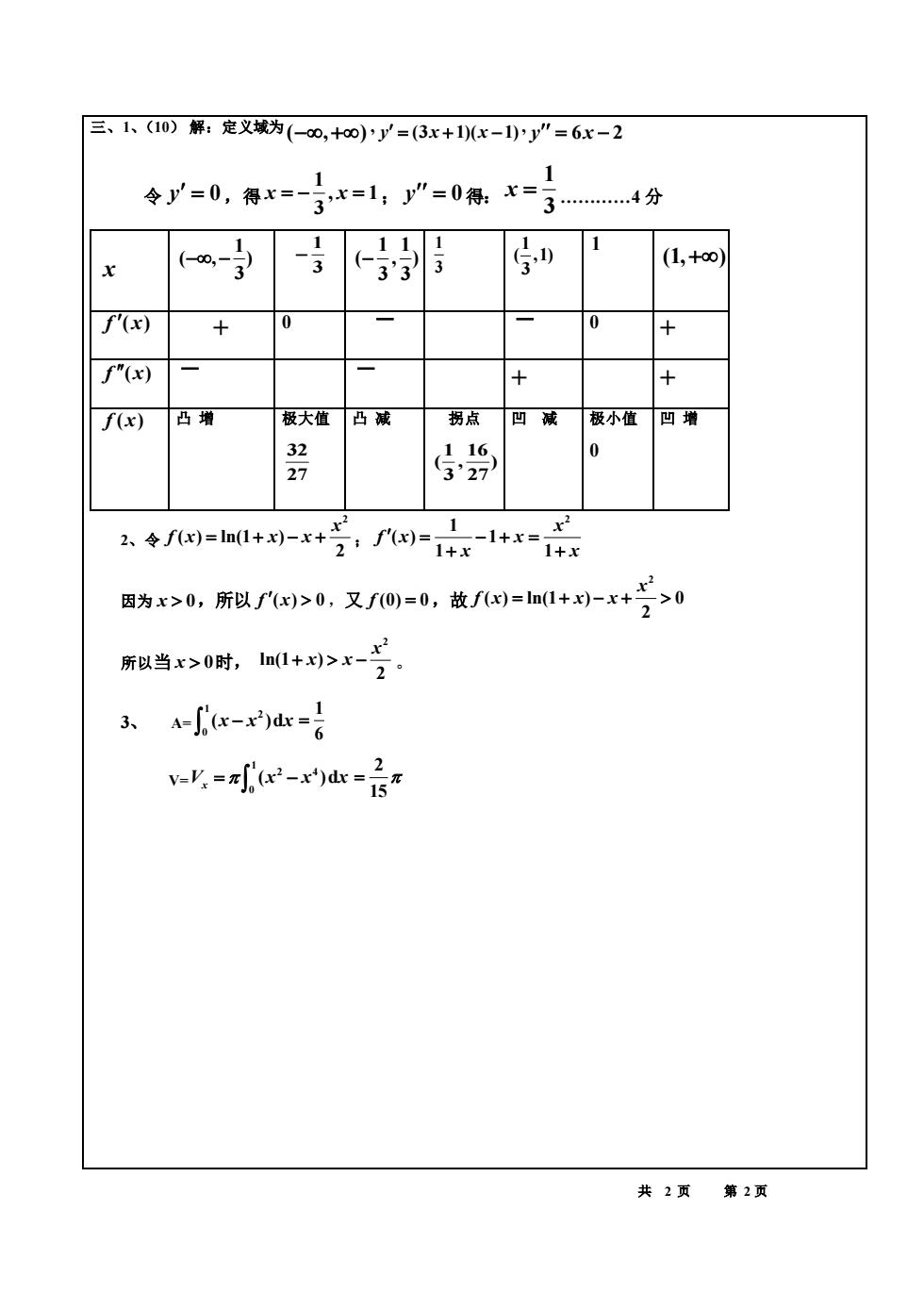
三、1、(10)解:定义域为(-0,+o0)y=(3x+1(x-1)y”=6x-2 令广=0,得x=-了x=1,”=0得r=34分 11 (00. -3 (1,+o0 3’3 3 f'(x) 0 0 + f"(x) + f(x) 凸增 极大值 凸 拐点 四减 极小值 凹增 0 1 2 2、令f(x)=ln(1+x)-x+ 1+x 1+x=1+x 因为x>0,所以fx)>0,又f0)=0,故了=ln1+-x+ 2>0 所当>0时,1+>x- 子A小x-=君 y=对e-=6 共2页第2页
共 2 页 第 2 页 三、1、(10) 解:定义域为 ( , ) − + , y x x = + − (3 1)( 1) , y x = − 6 2 令 y = 0 ,得 1 , 1 3 x x = − = ; y = 0 得: 1 3 x = .4 分 x 1 ( , ) 3 − − 1 3 − 1 1 ( , ) 3 3 − 1 3 1 ( ,1) 3 1 (1, ) + f x ( ) + 0 − − 0 + f x ( ) − − + + f x( ) 凸 增 极大值 32 27 凸 减 拐点 1 16 ( , ) 3 27 凹 减 极小值 0 凹 增 2、令 2 ( ) ln(1 ) 2 x f x x x = + − + ; 2 1 ( ) 1 1 1 x f x x x x = − + = + + 因为 x 0 ,所以 f x ( ) 0 ,又 f (0) 0 = ,故 2 ( ) ln(1 ) 0 2 x f x x x = + − + 所以当 x 0 时, 2 ln(1 ) 2 x + − x x 。 3、 A= 1 2 0 ( )d x x x − 1 6 = V= 1 2 4 0 V x x x x = − ( )d 2 15 =