《复变函数与积分变换》课程教学资源（PPT课件）第三章 复变函数的积分 3.6 第六节 高阶导数

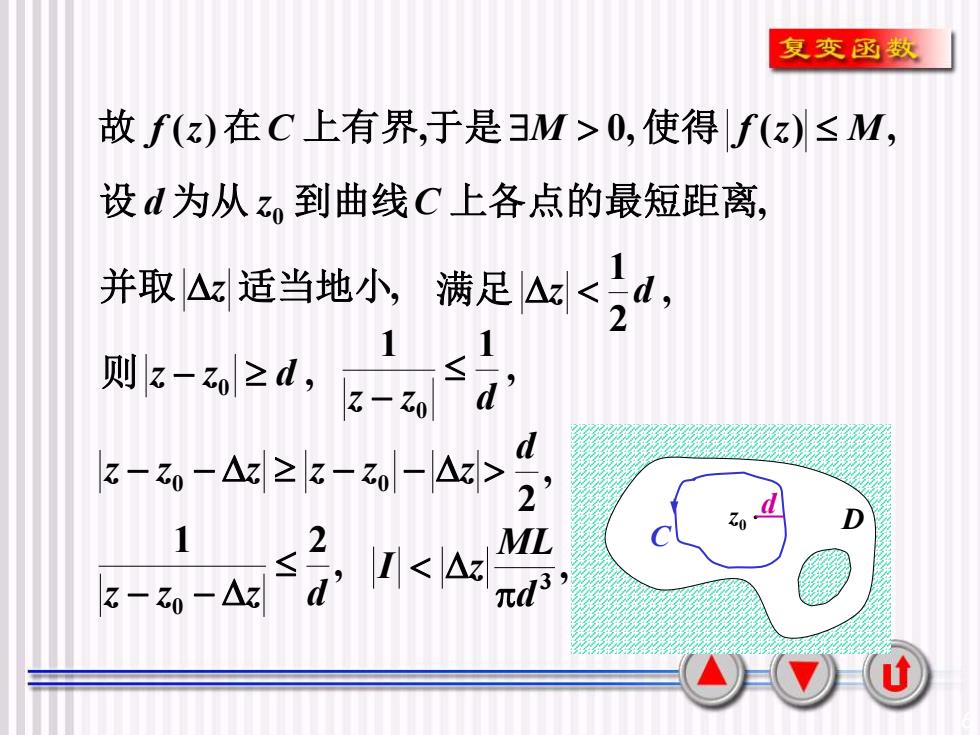
复变函数故f(z)在C 上有界,于是M >0,使得Lf(z)≤M,设d为从Z到曲线C上各点的最短距离并取△z适当地小,满足△z<2dLS则z -zo≥ d ,Z- ZodZo≥Zoz>2dDZoML121<<Azz,Td3Z- Zo -△zu

6 故 f (z)在C 上有界,于是 M  0,使得 f (z)  M, z0  D C , 设d 为从 z0 到曲线C 上各点的最短距离d 并取 z 适当地小, , 2 1 满足 z  d , 则 z − z0  d , 1 1 z z0 d  − 0 0 z − z − z  z − z − z , 2 d  , 1 2 z z0 z d  − −  , 3 d ML I z   

复变函数MLI<Az这里L为C的长度Td3,那末 I→0,如果z→0,f(z)f(zo +△z) - f(zo)f(zo) = limdz,2元iJc(z - zo)2Az4z-0f'(zo + △z) - f'(zo)lim再利用以上方法求极限AzAz-→02!f(z)可得 f"(zo)=dz.32元iJc(z - Zo)U

7 , 3 d ML I z    这里L为C的长度. 如果z → 0, 那末 I → 0, z f z z f z f z z  +  −  =  → ( ) ( ) ( ) lim 0 0 0 0 d , ( ) ( ) 2 1 2 0   − = C z z z f z i 再利用以上方法求极限 z f z z f z z   +  −   → ( ) ( ) lim 0 0 0 d . ( ) ( ) 2 2! ( ) 3 0 0   −  = C z z z f z i 可得 f z

复变函数至此我们证明了一个解析函数的导数仍然是解析函数依次类推，利用数学归纳法可证f(z)n!f(n)(zo)[证毕]2mi e( - .)l dz.)=高阶导数公式的作用不在于通过积分来求导，而在于通过求导来求积分

8 至此我们证明了一个解析函数的导数仍然是解 析函数. 依次类推, 利用数学归纳法可证 d . ( ) ( ) 2 ! ( ) 1 0 0 ( )  +  − = C n n z z z f z i n f z [证毕] 高阶导数公式的作用: 不在于通过积分来求导, 而在于通过求导 来求积分

复变函数三、典型例题例1 计算下列积分,其中C为正向圆周:z= r>1.erCOS元z(1) fc(2) fc (2 +1)(dz;dz.(z-1)COS元Z解 (1)函数在C内z=1处不解析(z-1)但cOS 元z在C内处处解析f(z)n!根据公式 (n)(zo)=dz2元i Jc(z- z0)1+1U

9 三、典型例题 例1 解   − +  =  C z C z z e z z z C z r d . ( 1) d ; (2) ( 1) cos (1) , : 1. 5 2 2 计算下列积分 其中 为正向圆周 1 , ( 1) cos (1)函数 5 在 内 = 处不解析 −  C z z z 但cosz 在C内处处解析,  +  − = C n n z z z f z i n f z d ( ) ( ) 2 ! ( ) 1 0 0 根据公式 ( )