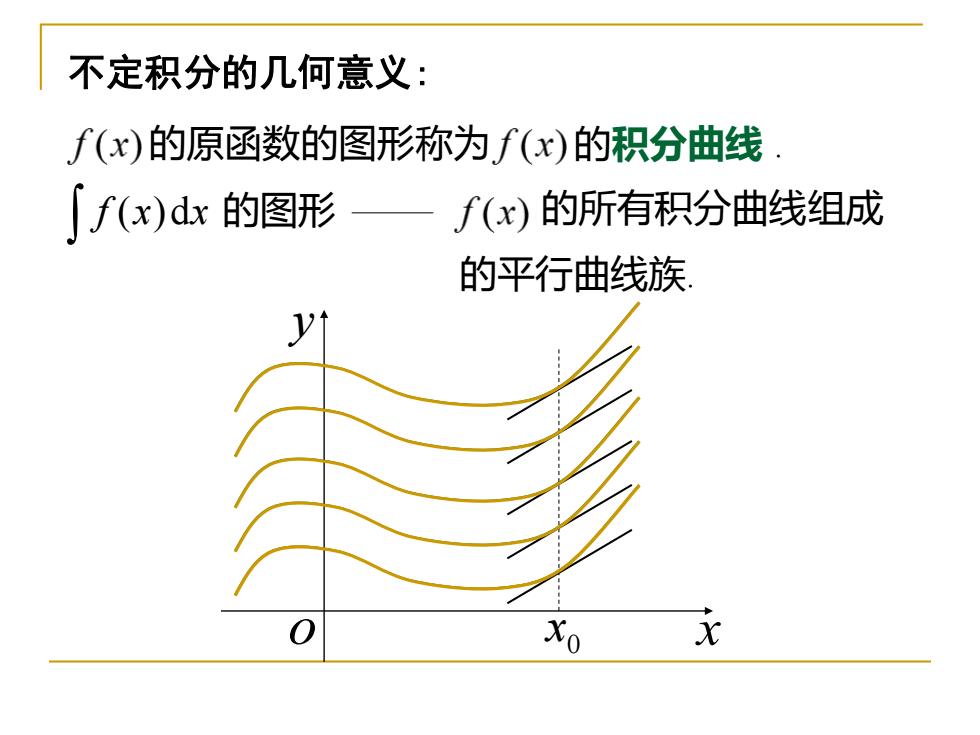
不定积分的几何意义: f(x)的原函数的图形称为f(x)的积分曲线 「f(x)dx的图形一 f(x)的所有积分曲线组成 的平行曲线族 Xo
不定积分的几何意义: 的原函数的图形称为 f (x)dx 的图形 的所有积分曲线组成 的平行曲线族. y o x0 x 的积分曲线
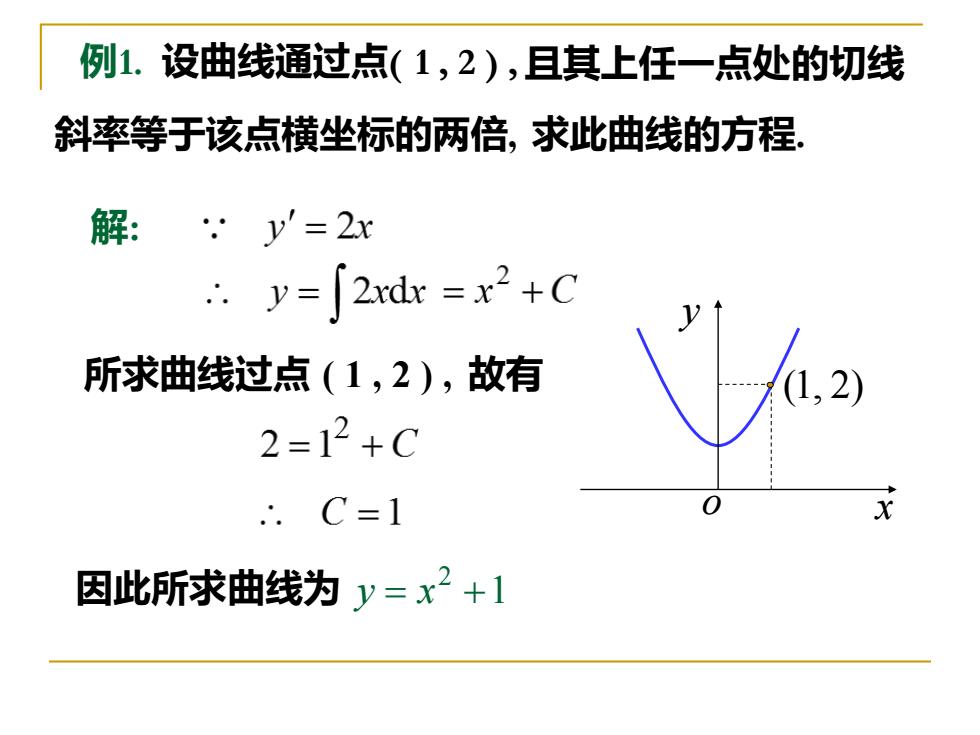
例1.设曲线通过点(1,2),且其上任一点处的切线 斜率等于该点横坐标的两倍,求此曲线的方程, 解:y'=2x .y=∫2de=x2+C 所求曲线过点(1,2),故有 2=12+C .C=1 因此所求曲线为y=x2+1
例1. 设曲线通过点( 1 , 2 ) , 且其上任一点处的切线 斜率等于该点横坐标的两倍, 求此曲线的方程. 解: 所求曲线过点 ( 1 , 2 ) , 故有 因此所求曲线为 1 2 y = x + y o x (1, 2)

二、 基本积分公式 利用逆向思维 ()「kdx=kx+C (k为常数) (2)∫xdr=x++C (4≠-1) x<0时 (3) (x)=[In(-x)-1 (4) dx 2 = arctanx+C -arccot x+C 1+x1 dx (5) arcsinx+C-arccosx+C /1-x
二、 基本积分公式 利用逆向思维 = (1) kdx kx +C ( k 为常数) = (2) x dx x +C + + 1 1 1 = x d x (3) ln x +C x 0时 ( −1) (ln x ) = [ln(−x)] x 1 = = + 2 1 d (4) x x arctan x +C 或 − arccot x +C = − 2 1 d (5) x x arcsin x +C 或 − arccos x +C