
线性代数敖程 第一章阶行列式 证当:位于第一行第一列时, 011 0 0 D= 21 l22 Q2n n 0n2. Ann 即有D-4M1 又A,=(-1)'M=Mm 从而D=41A 在证一般情形,此时
线性代数教程 线性代数小组 第一章 n阶行列式 证 当 ij 位于第一行第一列时, a n n nn n a a a a a a a D 1 2 21 22 2 11 0 0 = 即有 . D = a11M11 又 ( ) 11 1 1 A11 1 M + = − , = M11 从而 . D = a11A11 在证一般情形, 此时

线性代数教程 第一章阶行列式 411 avi n D= 0 吁 0 0n1. .Ann 把D的第行依次与第i-1行,第i-2行,第1行对调, 0 u 0 得D-((1-,1.a- .-l,n l m
线性代数教程 线性代数小组 第一章 n阶行列式 n nj nn ij j n a a a a a a a D 1 11 1 1 = 0 0 把D的第i行依次与第i −1行,第i − 2行,第1行对调, 得 ( ) n nj nn i i j i n ij i a a a a a a a D 1 1,1 1, 1, 1 0 0 1 − − − − = − ij a ij a

线性代数敖程 第一章阶行列式 再把D的第列依次与第j-1列,第j-2列,第1列 对调,得 0 . 0 D=(y.(yaw.awa l;-1,n Anj- m
线性代数教程 线性代数小组 第一章 n阶行列式 , 1 , 2 , 1 对调 再把D的第j列依次与第j − 列 第j − 列 第 列 得 ( ) ( ) nj n j nn i j i j i n ij i j a a a a a a a D , 1 1, 1, 1 1, 1 1 0 0 1 1 − − − − − − − = − − ij a
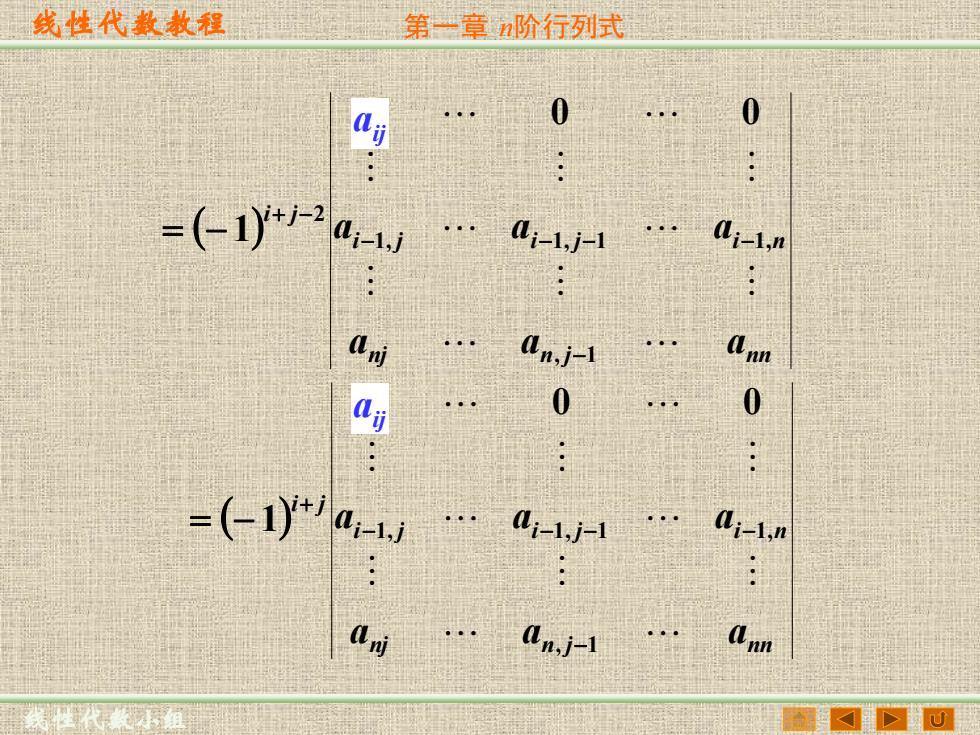
线性代教教程 第一章阶行列式 0 0 =(1-20.4w.-1月 l-1,” L n,j-1 Ann , 0 0 =()a- l-1,n w .0n,j-l Ann
线性代数教程 线性代数小组 第一章 n阶行列式 ( ) nj n j nn i j i j i n ij i j a a a a a a a , 1 1, 1, 1 1, 2 0 0 1 − − − − − + − = − ( ) nj n j nn i j i j i n ij i j a a a a a a a , 1 1, 1, 1 1, 0 0 1 − − − − − + = − ij a ij a