
第之节 第九章 多无菡数微分学的儿何应用 一、空间曲线的切线与法平面 二、曲面的切平面与法线 HIGH EDUCATION PRESS 上页下页返回结束
第六节 复习 目录 上页 下页 返回 结束 一、空间曲线的切线与法平面 二、曲面的切平面与法线 多元函数微分学的几何应用 第九章

复习:平面曲线的切线与法线 已知平面光滑曲线=f(x)在点(x01。)有 切线方程v-10=f'(o(x-Yo) 法线方程-'0= (-o f'(xo) 若平面光滑曲线方程为F(x,)=0.因 dr F(a.r) dr F(x) 故在点(0.0)有 切线方程 F(0,1o)(r-o)+F,(x00X-0)=0 法线方程 F(oox-xo)-F(xa16)(1-1%)=0 HIGH EDUCATION PRESS 机动目录上页下页返回结束
复习: 平面曲线的切线与法线 已知平面光滑曲线 切线方程 法线方程 若平面光滑曲线方程为 故在点 切线方程 法线方程 在点 有 有 因 机动 目录 上页 下页 返回 结束
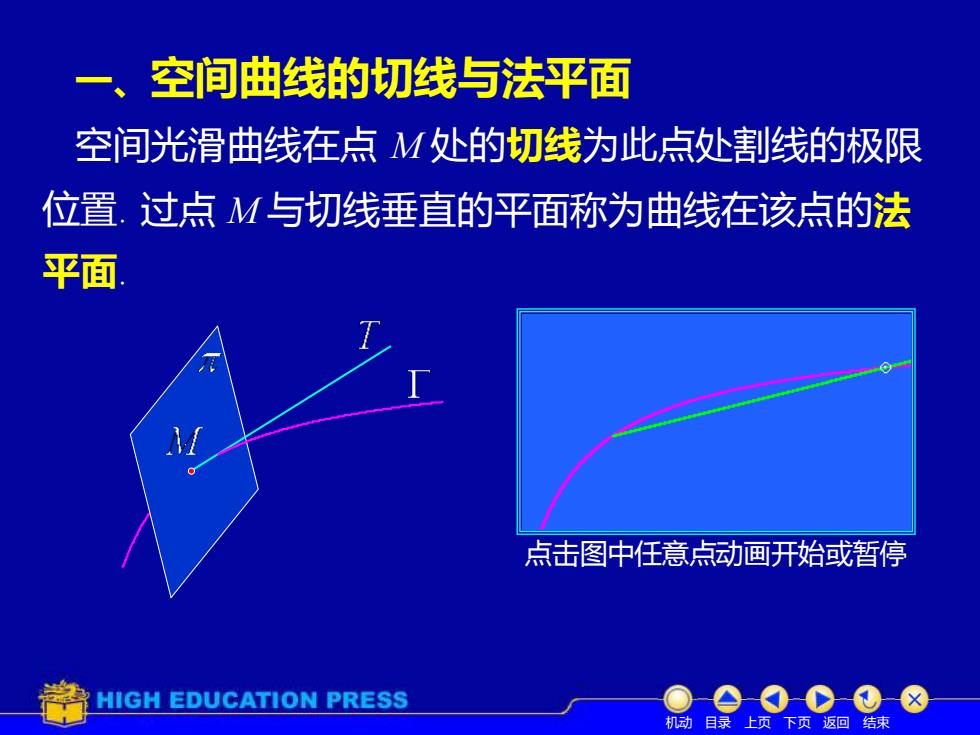
一、 空间曲线的切线与法平面 空间光滑曲线在点M处的切线为此点处割线的极限 位置.过点M与切线垂直的平面称为曲线在该点的法 平面 点击图中任意点动画开始或暂停 HIGH EDUCATION PRESS 机动目录上页下页返回结束
一、空间曲线的切线与法平面 过点 M 与切线垂直的平面称为曲线在该点的法 机动 目录 上页 下页 返回 结束 位置. 空间光滑曲线在点 M 处的切线为此点处割线的极限 平面. 点击图中任意点动画开始或暂停

1.曲线方程为参数方程的情况 T:x=0().1=y(1).三=0(1) 设1=1n对应1(0.)》 1=7。+△1对应'(x6+△.10十A.0+A=) 割线M'的方程: Y-X0=y-0=2-0 △N 4 4 上述方程之分母同除以1.令△1→0.得 切线方程 O(t) /(o) o(1o) HIGH EDUCATION PRESS 机动目录上页下页返回结束
1. 曲线方程为参数方程的情况 切线方程 机动 目录 上页 下页 返回 结束

此处要求o(t6).'(o).0'(t不全为0, 如个别为0,则理解为分子为0 切线的方向向量: T=(ooyo.0'U月 称为曲线的切向量 T也是法平面的法向量,因此得法平面方程 0(1a(x-X0)+/(t0)1-'片0'(1a-二)=0 说明:若引进向量函数r(t)=((1).().0(t),则T 为T()的矢端曲线,而在1。处的导向量 Fuo)=(o'16)./'(a).0'U) 就是该点的切向量 等HIGH EDUCATION PRESS 机动目录上页下页返回结束
此处要求 也是法平面的法向量, 切线的方向向量: 称为曲线的切向量 . 如个别为0, 则理解为分子为 0 . 机动 目录 上页 下页 返回 结束 不全为0, 因此得法平面方程 说明: 若引进向量函数 , 则 为 r (t) 的矢端曲线, 处的导向量 就是该点的切向量