导航 二、导数的几何意义 【问题思考】 1.如图,点2的坐标为c,fx),点P的坐标为cfc),直线PT为 曲线在点P处的切线 y=f(x)1
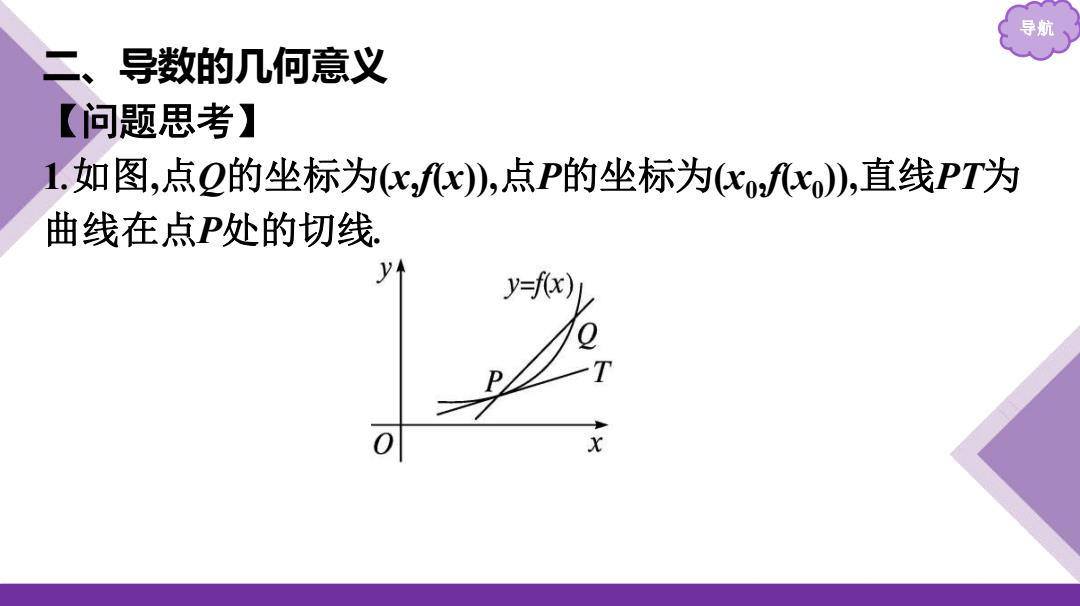
导航 二、导数的几何意义 【问题思考】 1.如图,点Q的坐标为(x,f(x)),点P的坐标为(x0 ,f(x0 )),直线PT为 曲线在点P处的切线

导航 ()割线PQ的斜率k是多少? 提示:kfx)-fxo x-x0 (2)当点Q无限趋近于点P时,割线PQ的斜率k与切线PT的斜率 kP有什么关系? 提示:k无限趋近于kPr
导航 (1)割线PQ的斜率k是多少? 提示:k=𝒇(𝒙)-𝒇(𝒙𝟎) 𝒙-𝒙𝟎 . (2)当点Q无限趋近于点P时,割线PQ的斜率k与切线PT的斜率 kPT有什么关系? 提示:k无限趋近于kPT

2.填空:如果将函数y=fx)的图象看成曲线(称为曲线y=x),而 且曲线在点Acx)处的切线为L,则△x很小时,Bc+△x, fKo+△x)是A附近的一点,割线AB的斜率是 △f- △X fxo+Ax)-f(xo),则当△x无限接近于0时,割线的斜率将 △X 无限趋近于切线的 ,这就是说, 就是曲线y=fx)在 点(cx)处(也称在x=x处)的切线的斜率,切线的方程是
导航 2.填空:如果将函数y=f(x)的图象看成曲线(称为曲线y=f(x)),而 且曲线在点A(x0 ,f(x0 ))处的切线为l,则Δx很小时,B(x0+Δx, f(x0+Δx))是A附近的一点,割线AB的斜率是 𝚫𝒇 𝚫𝒙 = 𝒇(𝒙𝟎 +𝚫𝒙)-𝒇(𝒙𝟎) 𝚫𝒙 ,则当 Δx 无限接近于 0 时,割线的斜率将 无限趋近于切线l的 斜率 .这就是说, f'(x0 ) 就是曲线y=f(x)在 点(x0 ,f(x0 ))处(也称在x=x0处)的切线的斜率,切线的方程是 y-f(x0 )=f'(x0 )(x-x0 )

3.做一做:已知函数y=fx)的图象如图所示,则fc)与fx)的 大小关系是( AfcA≥f'cB) B.f(x)f) Cf比A=f'xB) D.不能确定 XB XA 答案:B 解析:由图象易知,点A,B处的切线的斜率k4,kg满足k4<kB<0, 由导数的几何意义,可知fc)f'心B)
导航 3.做一做:已知函数y=f(x)的图象如图所示,则f'(xA )与f'(xB )的 大小关系是( ) A.f'(xA )>f'(xB ) B.f'(xA )<f'(xB ) C.f'(xA )=f'(xB ) D.不能确定 答案:B 解析:由图象易知,点A,B处的切线的斜率kA ,kB满足kA<kB<0. 由导数的几何意义,可知f'(xA )<f'(xB )