
第八节多元函数的极值与拉格朗日乘数法多元函数的极值和最值1条件极值拉格朗日乘数法■小结思考题
◼ 多元函数的极值和最值 ◼ 条件极值 拉格朗日乘数法 ◼ 小结 思考题 第八节 多元函数的极值与 拉格朗日乘数法

一、多元函数的极值和最值1.极大值和极小值的定义一元函数的极值的定义:是在一点附近将函数值比大小定义设在点P,的某个邻域,f(P)<(P),则称点P.为函数的极大值点.f(P)为极大值类似可定义极小值点和极小值
一、多元函数的极值和最值 一元函数的极值的定义:是在一点附近 将函数值比大小. 定义 点P0为函数的极大值点. 类似可定义极小值点和极小值. 设在点P0的某个邻域, ( ) ( ), P0 f P f 为极大值. 则称 ( ) P0 f 1. 极大值和极小值的定义

极值函数的极大值与极小值统称为函数的函数的极大值点与极小值点统称为函数的极值点注多元函数的极值也是局部的,是与P的邻域内的值比较般来说:极大值未必是函数的最大值-极小值未必是函数的最小值有时极小值可能比极大值还大
注 函数的极大值与极小值统称为函数的 函数的极大值点与极小值点统称为函数的 多元函数的极值也是局部的, 一般来说:极大值未必是函数的最大值. 极小值未必是函数的最小值. 有时 , 极值. 极值点. 内的值比较. 是与P0的邻域 极小值可能比极大值还大
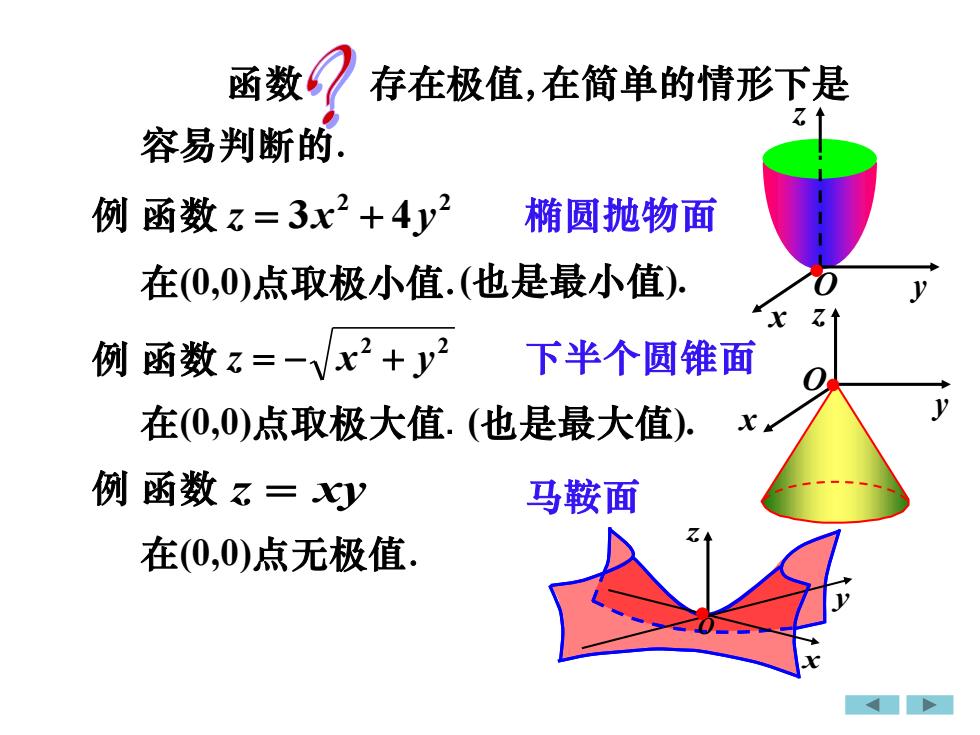
函数存在极值,在简单的情形下是7.容易判断的。例函数z=3x2+4y椭圆抛物面在(0,0)点取极小值.(也是最小值)0yZ.例 函数=2+2下半个圆锥面V在(0,0)点取极大值.(也是最大值)x例 函数 z = xy马鞍面L在(0,0)点无极值
x y z O x y z O 例 2 2 z = 3x + 4y 例 2 2 z = − x + y 例 z = xy 函数 存在极值, 在(0,0)点取极小值. 在(0,0)点取极大值.(也是最大值). 在(0,0)点无极值. 椭圆抛物面 下半个圆锥面 马鞍面 在简单的情形下是 容易判断的. 函数 函数 (也是最小值). 函数 • • x y z O •

2.极值的必要条件定理1(必要条件)设函数z= f(x,y)在点(xo,Jo)具有偏导数,且在点(xo,)处有极值,则它在该点的偏导数必然为零:f,(xo, yo)= 0.fr(xo,yo) = 0,证 不妨设z= f(x,J)在点(xo,Jo)处有极大值,则对于(xo,yo)的某邻域内任意(x,)≠(xo,Jo),都有f(x,y)< f(xo,yo),故当y= yo,x± x,时,有f(x, yo) < f(xo, yo),说明一元函数f(x,y)在x=x,处有极大值必有 f(xo,yo)=0;类似地可证f,(xo,Jo)=0
证 定理1(必要条件) ( , ) ( , ) 0 0 设函数z = f x y 在点 x y 具有 且在点(x0 , y0 )处 则它在该 点的偏导数必然为零: ( , ) 0, f x x0 y0 = ( , ) 0. f y x0 y0 = 偏导数, 有极值, 不妨设 z = f (x, y)在点(x0 , y0 )处 有极大值, 则对于(x0 , y0 )的某邻域内任意( , ) ( , ), 0 0 x y x y 都有 ( , ) ( , ), 0 0 f x y f x y , , 故当y = y0 x x0时 ( , ) ( , ), 0 0 0 有f x y f x y 说明一元函数 f (x, y0 )在x = x0处 有极大值, 必有 ( , ) 0; f x x0 y0 = ( , ) 0. 类似地可证 f y x0 y0 = 2. 极值的必要条件