解析函数 冬若w=fa)=uy)以+iv,以,,y)∈D,则 有极限 有极限 连续 连续 u=u(x,y以 w=f)在zo V=V(,y以 可导 可导 lexu@mail.xidian.edu.cn 复变函数●)
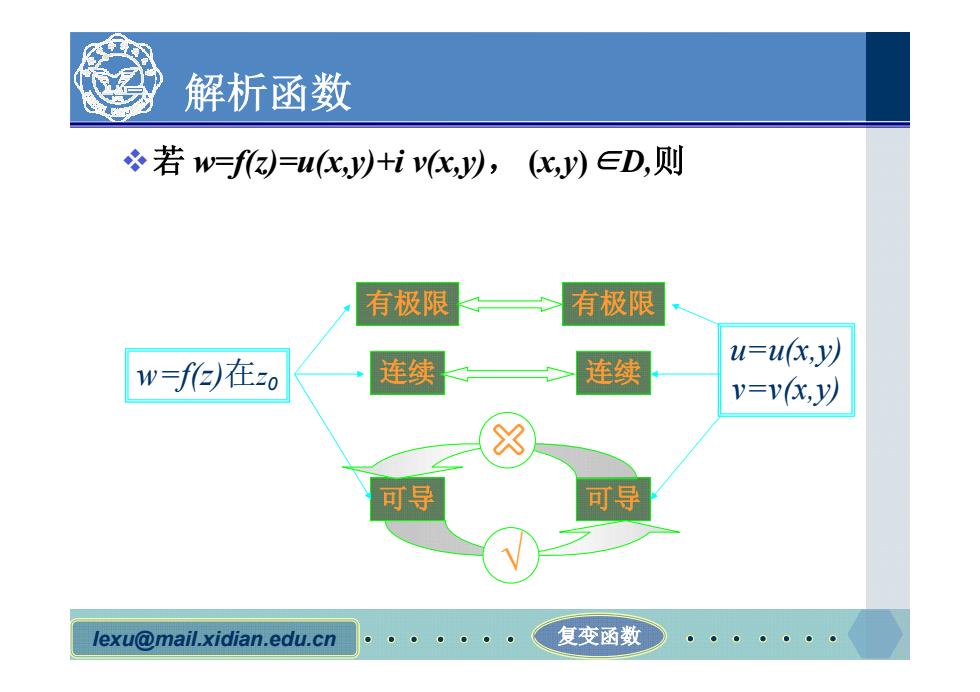
lexu@mail.xidian.edu.cn 复变函数 解析函数 v若 w=f(z)=u(x,y)+i v(x,y), (x,y)∈D,则 w=f(z)在z0 有极限 连续 可导 u=u(x,y) v=v(x,y) 有极限 连续 可导 √ ×
解析函数 在D内解析 u Ov ax oy'dy 在D内可导 Ox 8 8 在z内解析 在z内可导 在z处连续 lexu@mail.xidian.edu.cn 复变函数 。。●。●0
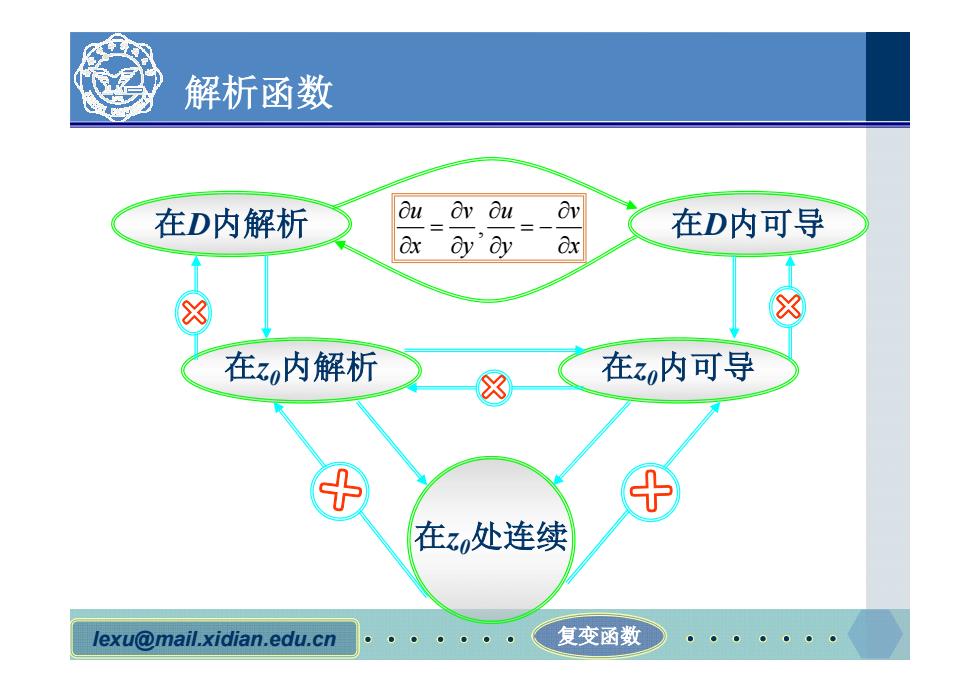
lexu@mail.xidian.edu.cn 复变函数 解析函数 在D内解析 在D内可导 在z0内解析 在z0内可导 在z0处连续 × × × × × , u v u v x y y x

解析函数 下=y(x,y)x+v,(x,y)) f(2)=v 冬平面流速场的复势 f(2)=o(x,y)+iv(x,y) oo(x,y) 二vx au(x,y) Ox Ox rot= divy ay二0 oo(x,y) ou(x,y) 8y ay vx E=E+E, E=-if'() 静电场的复势 f(=)=u(x,y)+iv(x,y) E Ov Ou OE,OE=0 Ox E 0x oy av divE-迟+E,-d E ou ax dy lexu@mail.xidian.edu.cn 复变雷数
lexu@mail.xidian.edu.cn 复变函数 解析函数 v平面流速场的复势 v静电场的复势 ( , ) ( , ) ˆ ˆ x y v v x y x v x y y ( , ) ( , ) x y x y v x x y v y div 0 x y v v v x y ( , ) ( , ) y x x y v x x y v y rot 0 y x v v v x y f z x y i x y ( ) ( , ) ( , ) f z v '( ) ˆ ˆ E E x E y x y rot 0 y x E E E x y x y v E x v E y div 0 Ex Ey E x y y x u E x u E y f z u x y iv x y ( ) ( , ) ( , ) E i f z '( )