
场论与复变函数 复变函数篇 主讲:徐乐
场论与复变函数 复变函数篇 主讲:徐乐

复数概论 复数 复数的表示 冬复数的运算 冬复球面 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 2 复数概论 复数 复数的表示 复数的运算 复球面
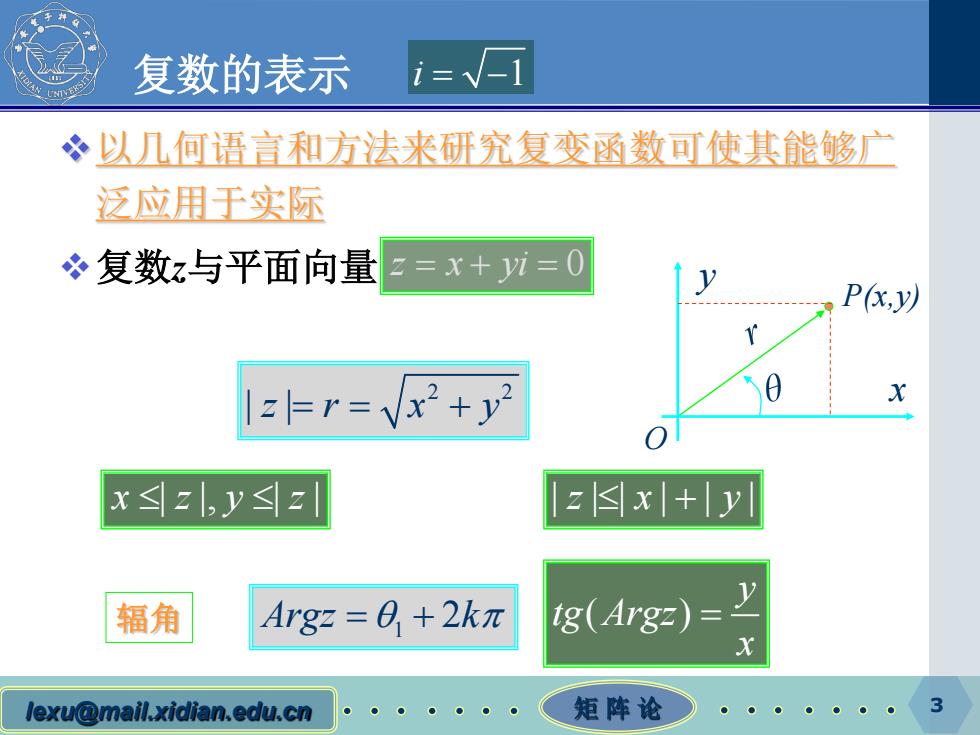
复数的表示 冬以几何语言和方法来研究复变函数可使其能够广 泛应用于实际 冬复数z与平面向量 z=x+yi=0 Px,y以 =vx2+y2 2 x≤z,yz zx+y 辐角 Argz=O+2kπ tg(Argz) lexu@mail.xidian.edu.cn 矩阵论 3
lexu@mail.xidian.edu.cn 矩 阵 论 3 复数的表示 以几何语言和方法来研究复变函数可使其能够广 泛应用于实际 复数z与平面向量 2 2 | | zr x y = = + x y P(x,y) O x zy z ≤ ≤ | |, | | | || | | | zx y ≤ + ( ) y tg Argz x 辐角 = 1 Argz k = + θ π 2 z x yi =+ = 0 i = −1

复数的表示 辐角主值的计算 π y.π =arg < 2 arc tg x 2 are ng x>0,y∈R x π x=0,y≠0 a82= 2 x<0,y≠0 arc tg y土T X π x<0,y=0 lexu@mail.xidian.edu.cn 矩阵论 4
lexu@mail.xidian.edu.cn 矩 阵 论 4 复数的表示 辐角主值的计算 argz = x y O x yR > ∈ 0, x y = ≠ 0, 0 x y < ≠ 0, 0 x y < = 0, 0 2 2 y arc tg x π π −< < 2 y arc tg x y arc tg x π π π ± ± 0 θ = argz
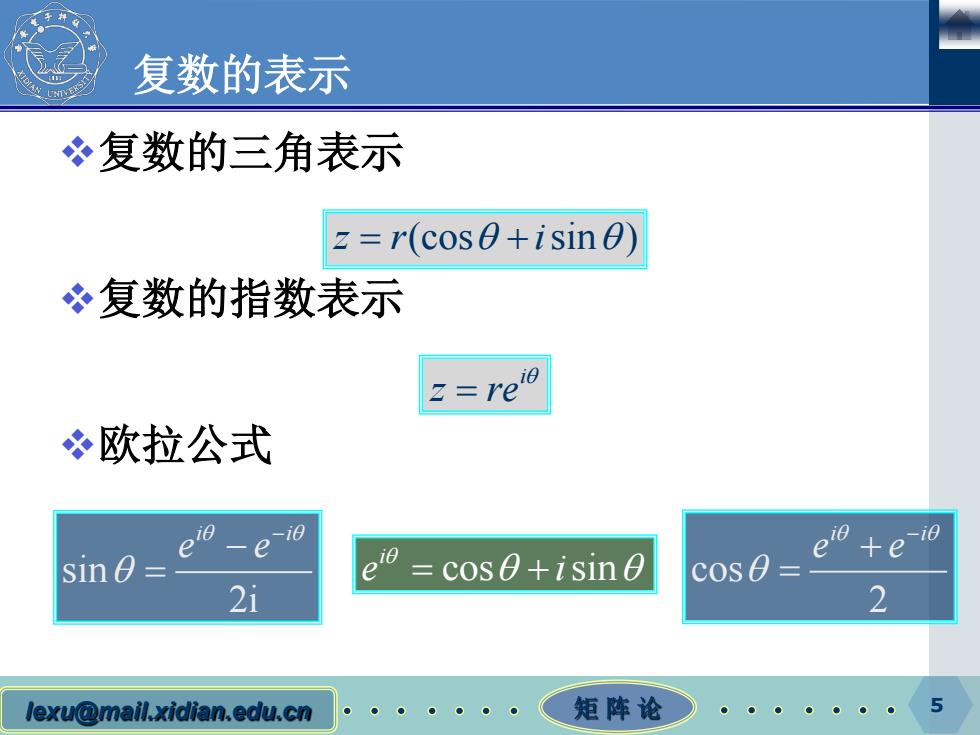
复数的表示 冬复数的三角表示 z=r(cosθ+isin0) 复数的指数表示 2=reio 冬欧拉公式 -e0 十e0 sin=- =cos0+isine CoS0=. 2i 2 lexu@mail.xidian.edu.cn 矩阵论
lexu@mail.xidian.edu.cn 矩 阵 论 5 复数的表示 复数的三角表示 复数的指数表示 欧拉公式 zr i = + (cos sin ) θ θ i z re θ = cos sin i e i θ = + θ θ cos 2 i i e e θ θ θ − + sin = 2i i i e e θ θ θ − − =