
西安电子科枝大学 电子工程学院《A School of Electronic Engineering.Xidian University http://see .xidian.edu.cn n.edu.ch 场论与复变函数 xuamail.x 主讲:徐乐 2011年11月6日星期日
lexu@mail.xidian.edu.cn

Review ■解析函数的充要条件 ■函数f回=(x,)+i,)在区域D内 ■u(x,y)和v(x,y)在区域D可微 an.edu.cx ■且在区域D满足柯西黎曼方程 ·[推论1]若fE)在区域D处处为零,则fP)在D内为常数 ·[推论2]f回=(x)计1x,)为解析函数,且f0, 则曲线族uGc,x,以=c必互相正交,其中 C,c2为常数 lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

解析函数的充要条件 可导复变函数在一点的导数公式 Ou Ov cidia f(z)= Ov Ou f()= +1 ou ov ou ox ey oy Ox Ov.Ov f'(z)= f'(z)= 一十1 ax ioy lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn
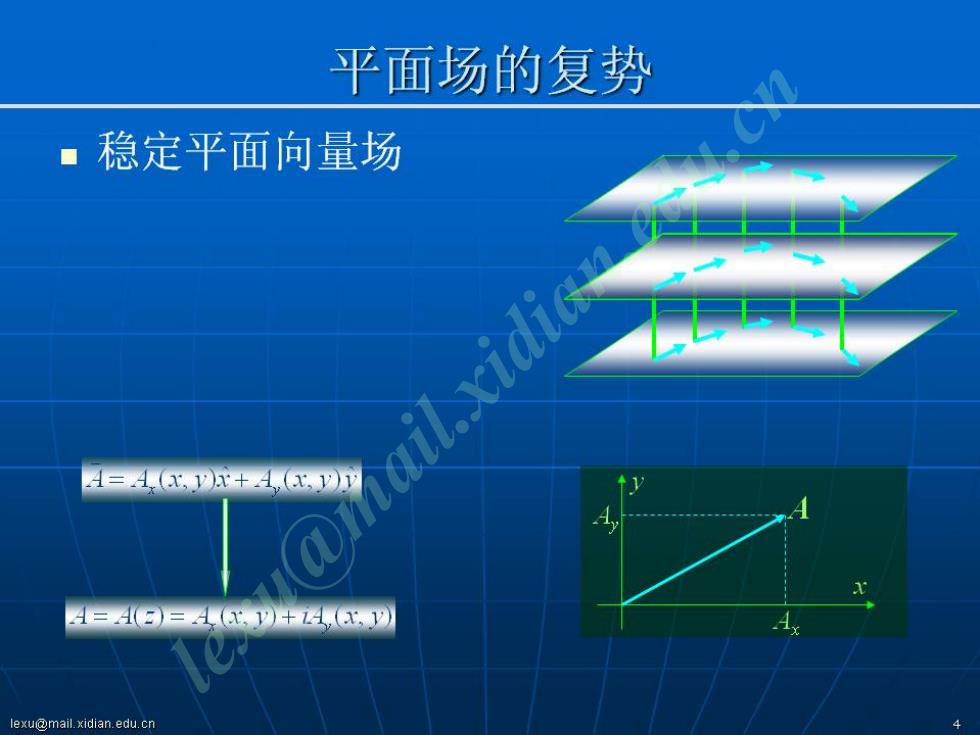
平面场的复势 ■稳定平面向量场 A=4,心+1x, A=()=1x,+,y lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn

平面场的复势 势函数 v=v(.Vx+v(T,vv f=y 流函数 平面流速场的复势 agp(x,y】 8v(x,y) Ov, Ox Ox Ov, rot拉= divv= + =0 Ox Oy o(x,y) ayW(x,】 三Vx d Cv E=EX+EY E=-if"】 静电场的复势 力函数 势函数 ou E Ov d div a腿4, ou =0 Ox Oy Oy E,= Ov E, OE=0 Oy ax lexu@mail.xidian.edu.cn
lexu@mail.xidian.edu.cn