
例1.设两个独立的随机变量X与Y都服从标准正态分布, 求Z=X+Y的概率密度。 解:因人田=1e若 2 -e2,-0<x<o0 1 2 f0)-2 e 2,-0o<y<00, -Eo-d e 2e 2 dx 2π =√π 即Z服从N(0,2)分布。 2√元
1. X Y Z X Y = + 例 设两个独立的随机变量 与 都服从标准正态分布, 求 的概率密度。 解:因 2 2 1 ( ) , 2 x X f x e x − = − 2 2 1 ( ) , , 2 y Y f y e y − = − 2 z 2 2 t x = − 1 4 2 d 2 z z x e e x − − − − = 2 2 4 1 d 2 z t e e t − − − 2 4 1 , 2 z e − = f z f x f z x x Z X Y ( ) ( ) ( )d − = − 2 2 ( ) 2 2 1 d 2 x z x e e x − − − − = 即Z N 服从 (0 2,)分布。 =

说明: (1)若X,Y相互独立且X~N(41,o),Y~N(42,o),则 X+Y~N(41+42,G1+G2). (2)若X:~N(,o)(i=1,2,.,m)且它们相互独立,则 2x-2n2 (3)有限个相互独立的正态随机变量的线性组合仍然服从正态 分布. 例如对(1)中的X,Y,有 aX+bY-N(am+buz,a'o+b2o2)
(3)有限个相互独立的正态随机变量的线性组合仍然服从正态 分布. 例如对(1) , 中的X Y,有 2 2 1 1 1 2 ~ ( , ) ( 1,2, , ) ~ ( , ) i i i n n n i i i i i i X N μ σ i n X N μ σ = = = = ( )若 且它们相互独立,则 说明: 2 2 1 1 2 2 2 2 1 2 1 2 1 , ~ ( , ), ~ ( , ) ~ ( , ). X Y X N μ σ Y N μ σ X Y N + + + μ μ σ σ ( )若 相互独立且 ,则 2 2 2 2 1 2 1 2 aX bY N a + + + ~ ( , ) μ b μ a σ b σ
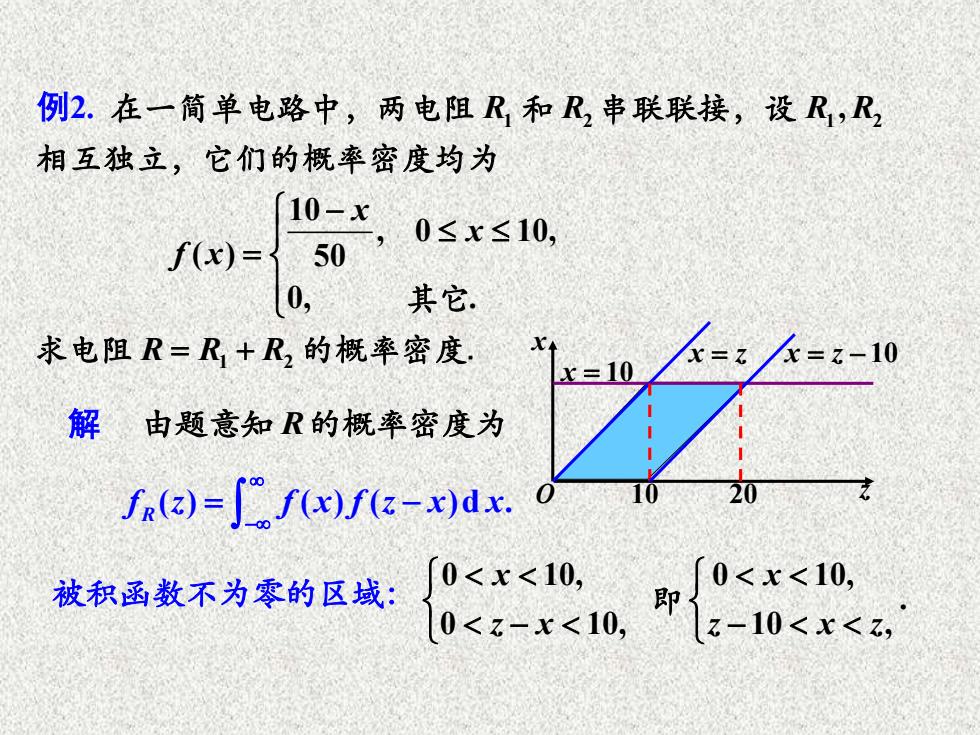
例2.在一简单电路中,两电阻卫1和几2串联联接,设R1,R2 相互独立,它们的概率密度均为 10-x 0≤x≤10, f(x)= 50 0, 其它 求电阻R=R+R,的概率密度. x=10 K=2k=z-10 解 由题意知R的概率密度为 ()-w)f(z-dx.o 被积函数不为零的区域: 0<x<10, 0<x<10, 0<z-x<10, 1-0<x<a
1 2 1 2 1 2 , 10 , 0 10, ( ) 50 0, . R R R R x x f x R R R − = = + 在一简单电路中,两电阻 和 串联联接,设 相互独立,它们的概率密度均为 其它 求电阻 的概率密度. 解 由题意知 R的概率密度为 ( ) ( ) ( )d . R f z f x f z x x − = − 例2. 0 10, 0 10, x z x − 0 10, . 10 , x z x z − 即 O 10 20 z x x = z x = z − 10 x = 10 被积函数不为零的区域: