
定义3:设向量值函数r=f()在1的某一邻域内有定义, 如果 △r lim lim f(。+△)-f() △1→0△t △1-→0 △t 存在,那么就称这个极限向量为向量值函数f(t)在1处 的导数或导向量,记作 f)或 dr 设f()=(f(t),f(,f(),t∈D,则 导数:f(0=(f),(),f()
定义3: 0 设向量值函数r f t t ( ) 在 的某一邻域内有定义, 如果 0 lim t r t 0 存在,那么就称这个极限向量为向量值函数 f t t ( )在 处 1 2 3 设 f t f t f t f t t D ( ) ( ( ), ( ), ( )), , 则 0 0 0 ( ) ( ) lim t f t t f t t 的导数或导向量,记作 0 0 d ( ) . d t t r f t t 或 导数: ( ) ( ( ), ( ), ( )) 1 2 3 f t f t f t f t

向量值函数的导数运算法则:P94) 设,下是可导向量值函数,C是常向量,c是任一常数 p(t)是可导函数,则 dC-o (2)Ici()=c'() (3)[i)±】=()±() (4)o)i=p'u)0+p)i) (⑤)0]=00+00 (6) 是I()x】=()x)+)x (7 dpt】=p'(u)[pt)]
向量值函数的导数运算法则: (P94) 设 u, v 是可导向量值函数, (t) 是可导函数, 则 C O t d d (1) (2) [ ( )] ( ) d d cu t c u t t (3) [ ( ) ( )] ( ) ( ) d d u t v t u t v t t (4) [ ( ) ( )] ( ) ( ) ( ) ( ) d d t u t t u t t u t t (5) [ ( ) ( )] ( ) ( ) ( ) ( ) d d u t v t u t v t u t v t t (6) [ ( ) ( )] ( ) ( ) ( ) ( ) d d u t v t u t v t u t v t t C 是常向量, c 是任一常数, (7) ( ) ( ) ( ) d d u t t u t t

向量值函数导数的几何意义: 在R3中,设7=f(①),t∈D的终端曲线为T, OM=f),O=f。+△) f(t) △7=f。+△0-f,) △7 mA=f) 1%△1 设f(,)≠0,则 f'(t)表示终端曲线在t处的一个切向量, 其指向与t的增长方向一致
向量值函数导数的几何意义: 在 R3中, 设 r f (t), t D 的终端曲线为 , M x z O y Δr ( )0 f t t r Δ Δ ( ), ( Δ ) 0 0 OM f t ON f t t N Δ ( Δ ) ( ) 0 0 r f t t f t ( ) Δ Δ lim 0 0 f t t r t t 表示终端曲线在t0处的一个切向量, 其指向与t 的增长方向一致. ( )0 f t 设 f (t0 ) 0 , 则 r
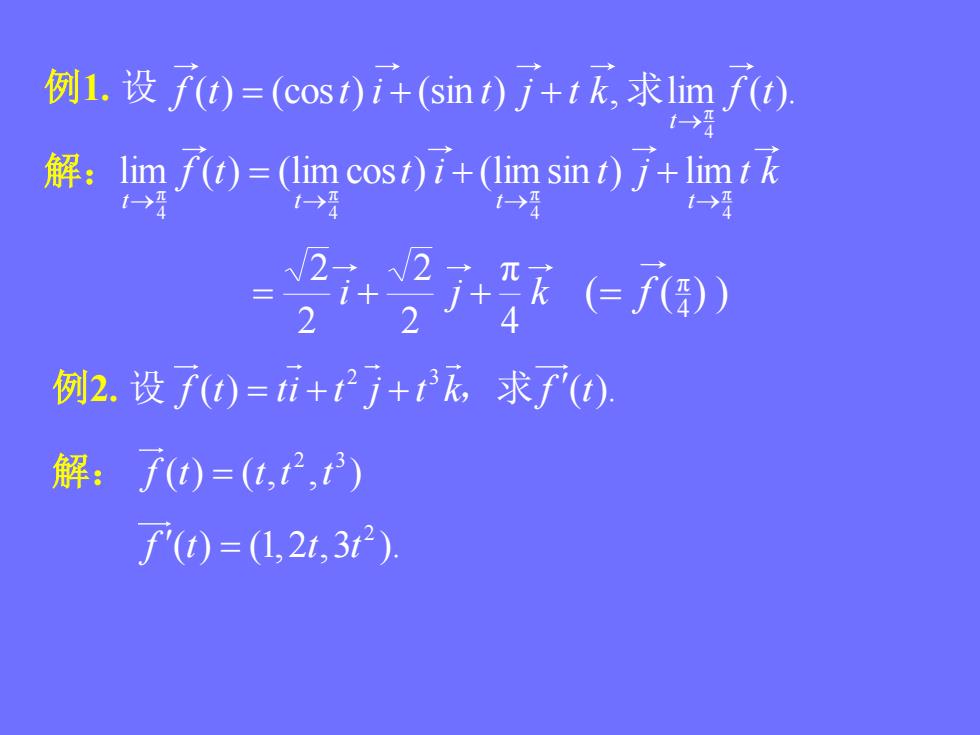
例1.设f0=(cos)i+(sin)j+t元,求1imft) 解:limf()=(lim cost)i+(lim sint)j+limt →1 - 例2.设f)=i+t2j+t元求f(0 解:f()=(,2,) f'(t)=(1,21,32)
( ) (cos ) (sin ) , lim ( ). 4 π f t t i t j t k f t t 例1. 设 求 解: f t t i t j t k t t t t 4 π 4 π 4 π 4 π lim ( ) (lim cos ) (limsin ) lim i j k 4 π 2 2 2 2 ( ( ) ) 4 π f 解: 例2. 设 2 3 f t ti t j t k f t ( ) ( ). ,求 2 3 f t t t t ( ) ( , , ) 2 f t t t ( ) (1,2 ,3 ).

例3.设空间曲线厂的向量方程为 7=f0=(t+1,4t-3,2r2-61),teR 求曲线厂上对应于t。=2的点处的单位切向量 解: f'(t)=(21,4,41-6),1∈R f'(2)=(4,4,-2》 f(2)=V42+4+(-2y2=6 f'(2) 221 故所求单位切向量为 f(2) 3’3’3 其方向与t的增长方向一致 另一与1的增长方向相反的单位切向量为(一 22 3-3
例3. 设空间曲线 的向量方程为 求曲线 上对应于 解: ( ) ( 1, 4 3, 2 6 ) 2 2 r f t t t t t 的点处的单位切向量. 故所求单位切向量为 其方向与 t 的增长方向一致 另一与 t 的增长方向相反的单位切向量为 ) 3 1 , 3 2 , 3 2 ( = 6