
第之为 第八章 空间曲线及其方程 一、空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影
第八章 一、空间曲线的一般方程 二、空间曲线的参数方程 三、空间曲线在坐标面上的投影 第六节 空间曲线及其方程
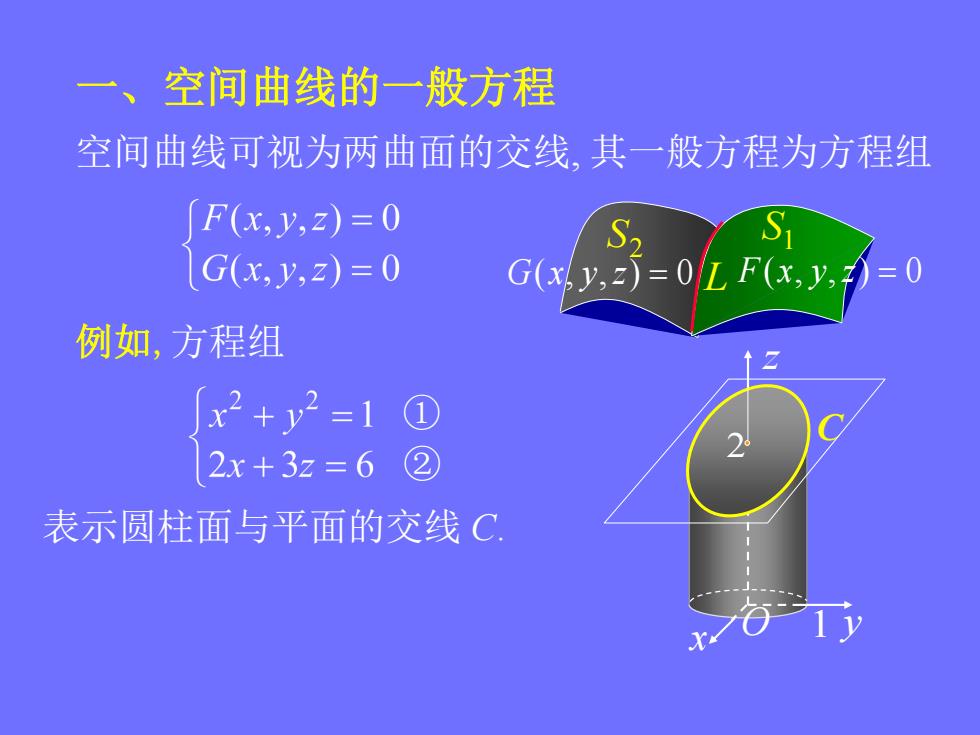
一、空间曲线的一般方程 空间曲线可视为两曲面的交线,其一般方程为方程组 F(x,y,2z)=0 G(x,y,z)=0 G(x.y. F(x,y,=0 例如,方程组 ↑☑ x2+y2=1① 2x+3z=6② 表示圆柱面与平面的交线C
一、空间曲线的一般方程 空间曲线可视为两曲面的交线, 其一般方程为方程组 S2 G(x, y,z) 0 L F(x, y,z) 0 S1 例如,方程组 表示圆柱面与平面的交线 C. x z O 1 y C 2 ① ②

又如,方程组 z-Va2-x2-y2 ① 1x2+y2-ax=0 ② (x- 2+y2= 4 表示上半球面与圆柱面的交线C
又如,方程组 表示上半球面与圆柱面的交线C. z y x a C ① ②

二、空间曲线的参数方程 将空间曲线C上的动点坐标x,y表示成参数1的函数: x=x(t) y=(t) (2) Z=Z(t) 当给定t=1时,就得到上的一个点(xy);随着1 的变动便可得曲线C上的全部点。 称方程组(2)为空间曲线的C参数方程
二、空间曲线的参数方程 将空间曲线C上的动点坐标 x, y, z表示成参数 t 的函数: 称方程组(2)为空间曲线的C参数方程. 当给定 时,就得到上的一个点 随着t 的变动便可得曲线C上的全部点。 (2)

例1 如果空间一点M在圆柱x2+y2=a 上以角速度o绕z轴旋转,同时 又以线速度沿平行于Z轴的正方向 上升,那么点M构成的图形叫螺旋 线。试求其参数方程。 M(x,y,Z 解得方程为: x=acoswt (x,0 y=asinat 令0=0t,b= x=acos z=vt y=asin z=b0 当0=2π时,上升高度h=2πb,称为螺距
z y x O v 令 t , b 上升高度 h 2π b, 称为螺距 . M 例1 如果空间一点M在圆柱 M / 2 2 2 x y a 上以角速度 绕 轴旋转,同时 又以线速度v沿平行于Z轴的正方向 上升,那么点M构成的图形叫螺旋 线。试求其参数方程。 N 解得方程为: