
设曲线 y=f(α),y= f,(x)yty= fi(x) y= f2(x)与直线 x=α,x=b(a<b)及x轴所围曲边梯形面积为Abxaxx+dxdA =fi(x)- f2(x)|dxA= (lfi(x) - f2(x) dxHIGH EDUCATION PRESS机动目录上页下页返回结束
1 2 d ( ) ( ) d A f x f x x = − 机动 目录 上页 下页 返回 结束 y o a b x ( ) 2 ( ) y = f x 1 y = f x A f x f x x b a ( ) ( ) d = 1 − 2 x x + d x 设曲线 与直线 及 x 轴所围曲边梯形面积为 A
例.计算两条抛物线y?=x, y=x在第一象限所围图形的面积解:由得交点(0,0),(1,1)T1(1.1)d A= (/x-x2)dxH店A= J(V-x)dxxx+dxHIGH EDUCATION PRESS机动目录上页下页返回结束
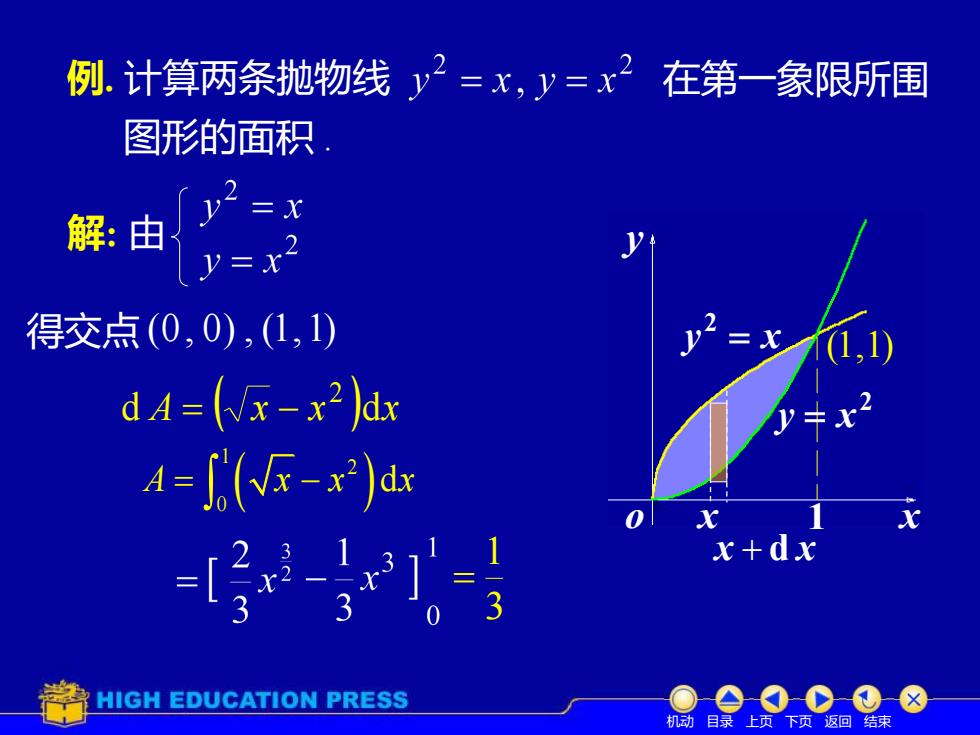
例. 计算两条抛物线 在第一象限所围 图形的面积 . x y = x 2 o y 2 y = x x x + d x 解: 由 得交点 (0, 0) , (1, 1) (1,1) 1 d A ( x x )dx 2 = − 3 1 = 机动 目录 上页 下页 返回 结束 ( ) 1 2 0 A x x x = − d

2=2x与直线 =x-4所围图形例.计算抛物线的面积=2x得交点解:由2xy=x-4(8,4)0+(2, -2),(8,4)为简便计算,选取y作积分变量x=x-4则有(y+4-{y)d)=[2+4y-3 ]-2=18HIGH EDUCATION PRESS机动目录上页下页返回结束
x y 2x 2 = o y y = x − 4 例. 计算抛物线 y 2x 2 = 与直线 的面积 . 解: 由 得交点 (2, − 2) , (8, 4) (8, 4) d A ( y 4 y )dy 2 2 1 = + − = 18 y = x − 4 所围图形 (2,− 2) 为简便计算, 选取 y 作积分变量, 则有 y y + d y − = 4 2 A 机动 目录 上页 下页 返回 结束

例.求椭圆所围图形的面积解:dA=ydxOydxA=4xx+dxa x利用椭圆的参数方程x= acost(0≤t≤2元)y=bsint应用定积分换元法得2bsint ·(-asint)dt = 4abtdtsin20元2=4αb.1.=πab当α=b时得圆面积公式2.2HIGH EDUCATION PRESS机动目录上页下页返回结束
a b o x y x 例. 求椭圆 解: d A = y dx 所围图形的面积 . = a A y x 0 4 d 利用椭圆的参数方程 (0 2 ) sin cos = = t y b t x a t 应用定积分换元法得 = 2 0 2 4 sin d ab t t = 4ab 2 1 2 = ab 当 a = b 时得圆面积公式 机动 目录 上页 下页 返回 结束 x + d x