2.区域 ()内点、外点、边界点 E 设有点集E及一点P: ·若存在,点P的某邻域U(P)cE, 则称P为E的内点; ●若存在,点P的某邻域U(P)∩E=☑, 则称P为E的外点; ·若对点P的任一邻域U(P)既含E中的内点也含E 的外点,则称P为E的边界点· 显然,E的内点必属于E,E的外点必不属于E,E的 边界,点可能属于E,也可能不属于E 2009年7月5日星期日 7 目录 上页今下页 返回
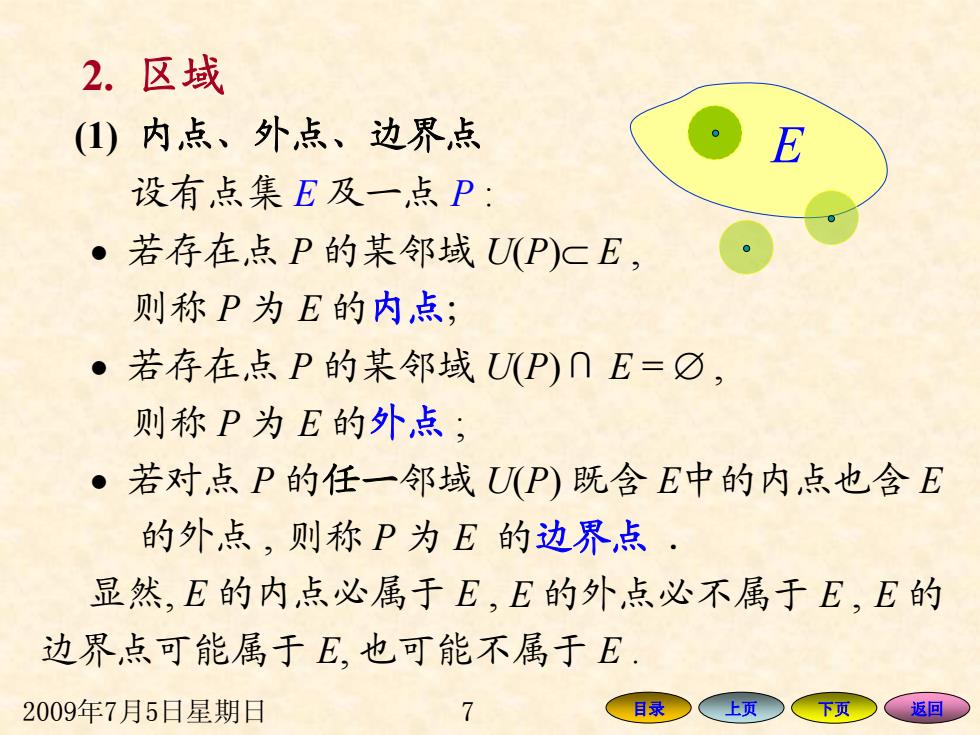
2009年7月5日星期日 7 目录 上页 下页 返回 (1) 内点、外点、边界点 设有点集 E 及一点 P : • 若存在点 P 的某邻域 U(P ) ⊂ E , • 若存在点 P 的某邻域 U(P ) ∩ E = ∅ , • 若对点 P 的任一邻域 U( P) 既含 E中的内点也含 E E 则称 P 为 E 的内点; 则称 P 为 E 的外点 ; 的外点 , 则称 P 为 E 的边界点 . 显然, E 的内点必属于 E , E 的外点必不属于 E , E 的 边界点可能属于 E, 也可能不属于 E . 2. 区域

(2)聚点 若对任意给定的δ,点P的去心 E 邻域U(P,δ)内总有E中的点,则 称P是E的聚点. 聚点可以属于E,也可以不属于E(因为聚点可以为 E的边界点) 所有聚点所成的点集成为E的导集 2009年7月5日星期日 8 目录○ 。上页 下页 、返回
2009年7月5日星期日 8 目录 上页 下页 返回 若对任意给定的 δ , 点 P 的去心 U P,( δ ) D E 邻域 内总有 E 中的点 , 则 称 P 是 E 的聚点. 聚点可以属于 E , 也可以不属于 E (因为聚点可以为 所有聚点所成的点集成为 E 的导集 . E 的边界点 ) (2) 聚点

(3)开区域及闭区域 ●若点集E的点都是内点,则称E为开集; ·E的边界,点的全体称为E的边界,记作OE; ·若,点集EOE,则称E为闭集; ·若集D中任意两点都可用一完全属于D的折线相连, 则称D是连通的; ·连通的开集称为开区域,简称区域; ·开区域连同它的边界一起称为闭区域 2009年7月5日星期日 9 目录 上页>下页 、返回
2009年7月5日星期日 9 目录 上页 下页 返回 D • 若点集 E 的点都是内点,则称 E 为开集; • 若点集 E ⊃∂E , 则称 E 为闭集; • 若集 D 中任意两点都可用一完全属于 D 的折线相连 , • 开区域连同它的边界一起称为闭区域. 则称 D 是连通的 ; • 连通的开集称为开区域 ,简称区域 ; . . • E 的边界点的全体称为 E 的边界, 记作 ∂E ; (3) 开区域及闭区域
例如,在平面上 {(xy)x+y>0} 开区域 {(x,y)1<x2+y2<4} ÷{(xy)x+y≥0} 闭区域 {(x,y)1≤x2+y2≤4} 2x 2x 2009年7月5日星期日 10 目录○ 、上页 (下页 返回
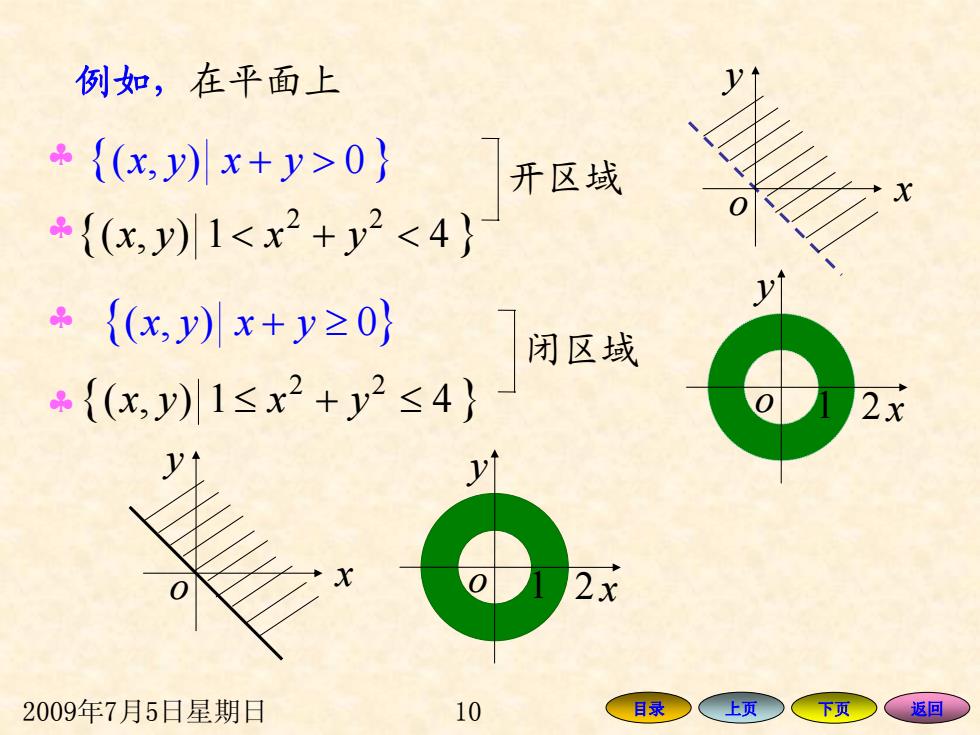
2009年7月5日星期日 10 目录 上页 下页 返回 { yxyx >+ 0),( } { 1),( 4 } 22 yxyx <+< { + yxyx ≥ 0),( } { 1),( 4 } 22 yxyx ≤+≤ 开区域 闭区域 ♣ ♣ ♣ ♣ x y o 1 2 x y o x y o x y o 1 2 例如,在平面上

品整个平面是最大的开域, 也是最大的闭域; 点集{(x,y)x>}是开集, 但非区域 ·对区域D,若存在正数K,使一切点PD与某定点 A的距离AP飞K,则称D为有界域,否则称为无 界域 2009年7月5日星期日 11 目录○ (上页今下页 、返回
2009年7月5日星期日 11 目录 上页 下页 返回 ♣ 整个平面 ♣ 点集 { xyx >1),( }是开集, 是最大的开域 , 也是最大的闭域; 但非区域 . − 1 o 1 x y • 对区域 D , 若存在正数 K , 使一切点 P ∈D 与某定点 A 的距离 ⎜AP⎥≤ K , 则称 D 为有界域 , 否则称为 无 界域