
新课引入 前面讨论的定积分,都是在有限区间上的有界函数 的积分,这类积分属于通常意义下的积分 但在实际问题中,还会遇到积分区间为无限或被积 函数在积分区间上是无界的情况, 这就需将定积分的概念推广,推广后的积分被称为 广义积分. 积分限有限 推广无穷限的广义积分 常义积分 被积函数有界◆无界函数的广义积分 2009年7月3日星期五 目录 上页 下页 返回
2009年7月3日星期五 1 目录 上页 下页 返回 新课引入 前面讨论的定积分,都是在有限区间上的有界函数 的积分,这类积分属于通常意义下的积分. 但在实际问题中,还会遇到积分区间为无限或被积 函数在积分区间上是无界的情况, 这就需将定积分的概念推广,推广后的积分被称为 广义积分. 常义积分 积分限有限 被积函数有界 推广 无穷限的广义积分 无界函数的广义积分

第五章 第四节广义积分 Improper Integrals) 一、无穷限的广义积分 二、无界函数的广义积分 三、思考与练习 2009年7月3日星期五 2 目录○ 、上页(下页 返回
2009年7月3日星期五 2 目录 上页 下页 返回 第四节 广义积分 第五章 (Improper Integrals) 二、无界函数的广义积分 一、无穷限的广义积分 三、思考与练习
一、无穷限(Infinite Intervals)的广义积分 引例曲线少平和直线-1及x锁所回成的并口曲 边梯形的面积可记作 y 其含义可理解为 -m8-1 2009年7月3日星期五 3 目录○ (上页今 下页 、返回
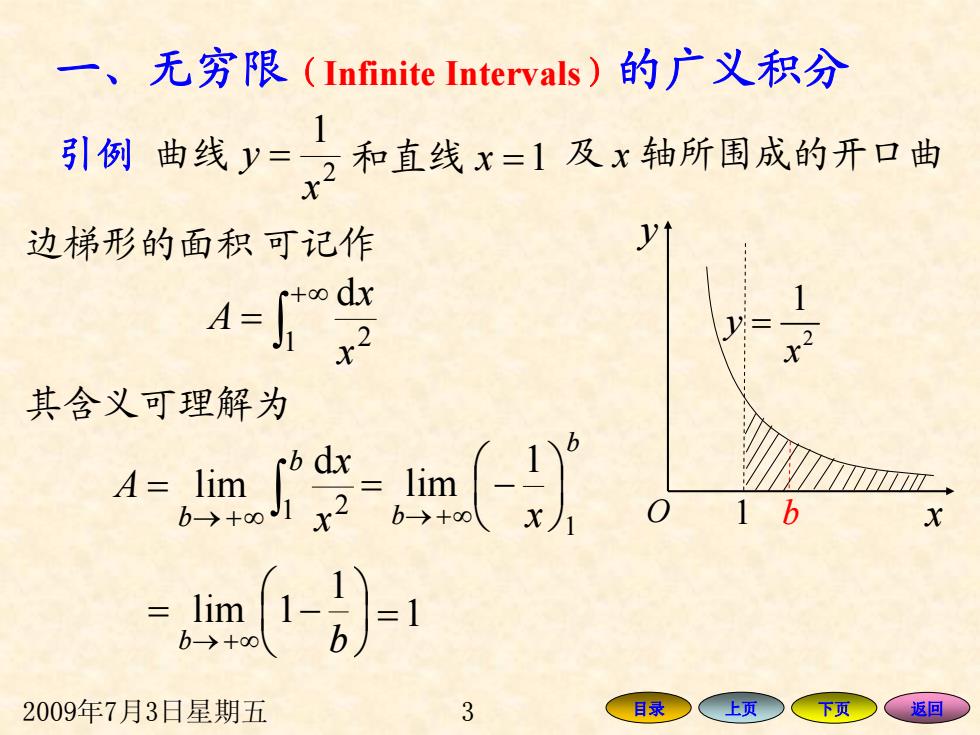
2009年7月3日星期五 3 目录 上页 下页 返回 一、无穷限 (Infinite Intervals )的广义积分 引例 曲线 2 1 x y = 和直线 x = 1 及 x 轴所围成的开口曲 边梯形的面积 可记作 ∫ ∞+ = 1 2 d x x A 其含义可理解为 ∫ ∞+→ = b b x x A 1 2 d lim b b x 1 1 lim ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −= ∞+→ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −= b ∞+→ b 1 1lim = 1 O x y 1 2 1 y x = b

定义1设f(x)∈C[a,+o),取b>a,若 nds 存在,则称此极限为f(x)的无穷限广义积分,记作 d-d 这时称广义积分∫f(x)dx收敛;如果上述极限不存在, 就称广义积分f(x)dr发散. 类似地,若f(x)∈C(-o,b],则定义 (x)dx=limf)dx 2009年7月3日星期五 4 目录 上页 下页 返回
2009年7月3日星期五 4 目录 上页 下页 返回 f ∈ aCx + ∞ ,),[)( 取 > ab , 若 xxf b b a∫ d)(lim∞+→ 存在 , 则称此极限为 f (x) 的无穷限广义积分, 记作 xxf xxf b a b a d)(limd)( ∫ ∫ ∞+→ + ∞ = 这时称广义积分 xxf a d)( ∫ + ∞ 收敛 ; 如果上述极限不存在, xxf a d)( 就称广义积分 ∫ + ∞ 发散 . 类似地 , 若 f x ∈ C − ∞ b ,],()( 则定义 xxf xxf b a a b d)(limd)( ∫ ∫ ∞− ∞−→ = 定义1 设

若f(x)∈C(-0,+o),则定义 「fd-lmfx)dx+mf)d (c为任意取定的常数) 只要有一个极限不存在,就称∫f(x)dx发散. 无穷限的广义积分也称为第一类广义积分 说明:上述定义中若出现0-0,并非不定型, 它表明该广义积分发散· 2009年7月3日星期五 5 目录 上页> 下页 、返回
2009年7月3日星期五 5 目录 上页 下页 返回 若 Cxf −∞∈ + ∞ ,),()( 则定义 = ∫ + ∞ ∞− d)( xxf xxf c a a∫ d)(lim∞−→ xxf b b c∫ d)(lim∞+→ + ( c 为任意取定的常数 ) 只要有一个极限不存在 , 就称 d)( xxf ∫ ∞+∞− 发散 . 无穷限的广义积分也称为第一类广义积分. 说明 : 上述定义中若出现 ∞ − ∞ ,并非不定型 , 它表明该广义积分发散