
第十八讲 全面最小二乘法
第十八讲 全面最小二乘法 1

一、法向回归 一组测量数据(,S),欲拟和直线 S=Ct+C2 2 最小二乘法采取目标函数:E(G,c2)=∑s,-ct,-c=min 它隐含了在测量中,,是精确测量的,只有S才测得不准确,而在 实际测量中,t,S都是无法准确测量的,因此,采用法向回归更有可 能。 2
一、 法向回归 一组测量数据( , ) i i t s ,欲拟和直线 1 2 s ct c = + 最小二乘法采取目标函数: ( ) 2 1 2 1 2 1 , min n i i i E c c s ct c = = −− = ∑ 它隐含了在测量中, i t 是精确测量的,只有 i s 才测得不准确,而在 实际测量中, i t , i s 都是无法准确测量的,因此,采用法向回归更有可 能。 2
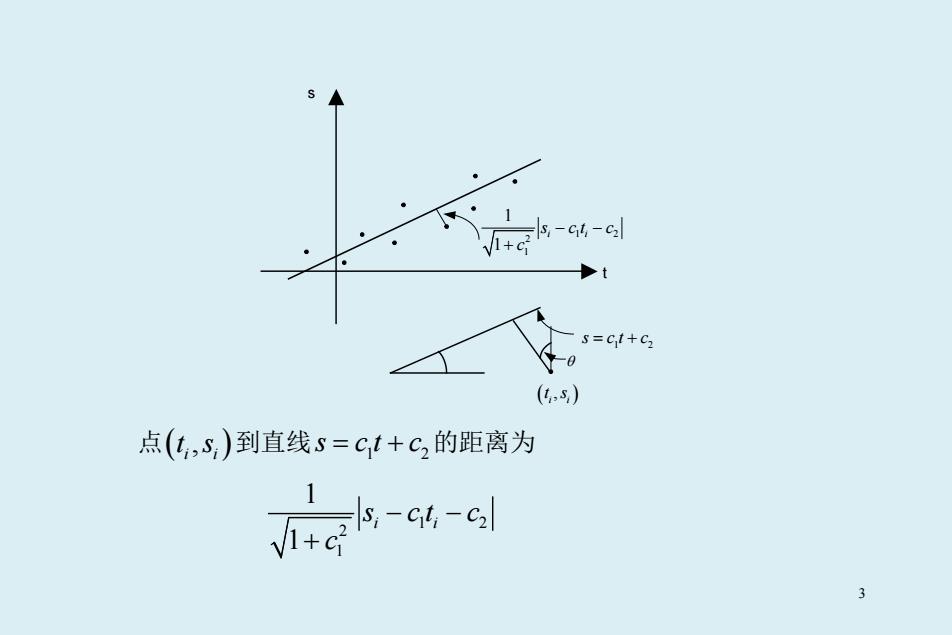
s,-ct,-cz t s=ct+C2 (4,) 点(,S)到直线s=ct+C,的距离为 以-d 3
1 2 2 1 1 1 i i s ct c c − − + t s θ 1 2 s ct c = + ( , ) i i t s 点( , ) i i t s 到直线 1 2 s ct c = + 的距离为 1 2 2 1 1 1 i i s ct c c − − + 3

故法向回归的目标函数为 aeeijg -c4,-c -min 1-2-26-6)=0之-4 OE OE 可立64280e-5-6l =22(e6s6c以-6) 4
故法向回归的目标函数为 ( ) 2 2 1 2 1 2 2 1 1 1 , min 1 n i i i E c c s ct c c = = −− = + ∑ ( )( ) 2 12 2 1 2 1 1 1 1 1 2 0 1 n n i i i i i i E s ct c c s ct c c = n = ∂ = − − − =→ = − ∂ + ∑ ∑ ( ) ( ) ( )( ) ( )( ) 2 1 2 1 2 2 1 2 2 1 1 1 1 1 2 12 1 1 2 1 1 2 2 1 1 2 1 n n i i ii i i i n ii i i i E c s ct c t s ct c c c c cc cs t s ct c c = = = ∂ = −− + − −− ∂ + + = − − −− + ∑ ∑ ∑ - 4
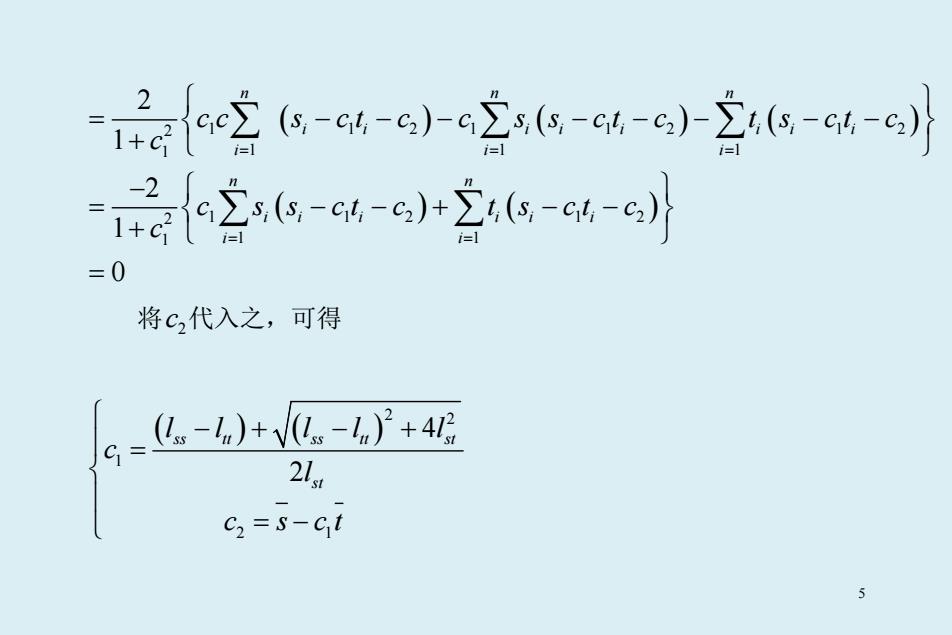
e空传-6)立g-e)aee} 12{空2a-6-o+e-c4-e} =0 将c2代入之,可得 _。-)+V。-)'+4 C 21. C2=s-Ct 5
( ) ( ) ( ) ( ) ( ) 2 1 1 21 1 2 1 2 1 1 11 2 1 12 1 2 1 1 1 2 1 2 1 0 n nn i i ii i ii i i ii n n ii i ii i i i cc s ct c c s s ct c t s ct c c c s s ct c t s ct c c = = = = = = −−− −−− −− + − = −−+ −− + = ∑ ∑∑ ∑ ∑ 将 2 c 代入之,可得 ( ) ( ) 2 2 1 2 1 4 2 ss tt ss tt st st ll ll l c l c s ct −+ − + = = − 5