
©中东X王大军 2、 矩阵加法的运算规律 ()A+B=B+A; (2)(A+B)+C=A+(B+C) -l12 一1n (3)-A= -0l22 =(-aj} 称为矩阵A的负矩阵 (④)A+(-A)=0,A-B=A+(-B) 上页
2、 矩阵加法的运算规律 (1) A+ B = B + A; (2)(A+ B)+ C = A+ (B + C). ( ) − − − − − − − − − − = m m m n n n a a a a a a a a a A 1 1 21 22 2 11 12 1 3 (4) A+ (− A) = 0, A− B = A+ (− B). ( ), = − aij 称为矩阵A的负矩阵

©少东理上大军 二、数与矩阵相乘 1、定义 数2与矩阵4的乘积记作乳A或A2,规定为 211 2L12 21n 2A=A2= 221 222 22n . Aam Aam Amn 区回
1、定义 . 1 1 2 1 2 2 2 1 1 1 2 1 = = m m mn n n a a a a a a a a a A A 二、数与矩阵相乘 数与矩阵A的乘积记作A或A,规定为

©中东罪工大至 运算规律 (设AB的是 柜阵, 2,μ∈R (1)1A=A (2)2(4A)=(24)A (3)(A+B)=A+2B (4)(2+四)A=元A+uA (5)0A=0 (6)20=0 注意:1)数乘矩阵是数去乘A中的每一个元素 2)若2A=,0测 2=0.0r.A=0 .0r.2=0.nd.A=O 矩阵的加法与数乘矩阵合称为矩阵的线性运算, 上页
2、运算规律 (设 A B C 均是 m n 矩阵, ) , R (1) 1A A = (2) ( ) ( ) A A = (3) ( ) A B A B + = + (4) ( ) + = + A A A (6) O O= 注意: 1)数乘矩阵是数λ去乘A中的每一个元素. (5) 0A O= 2)若 A O= ,则 = = = = 0 . . . . 0. . or A O or and A O 矩阵的加法与数乘矩阵合称为矩阵的线性运算
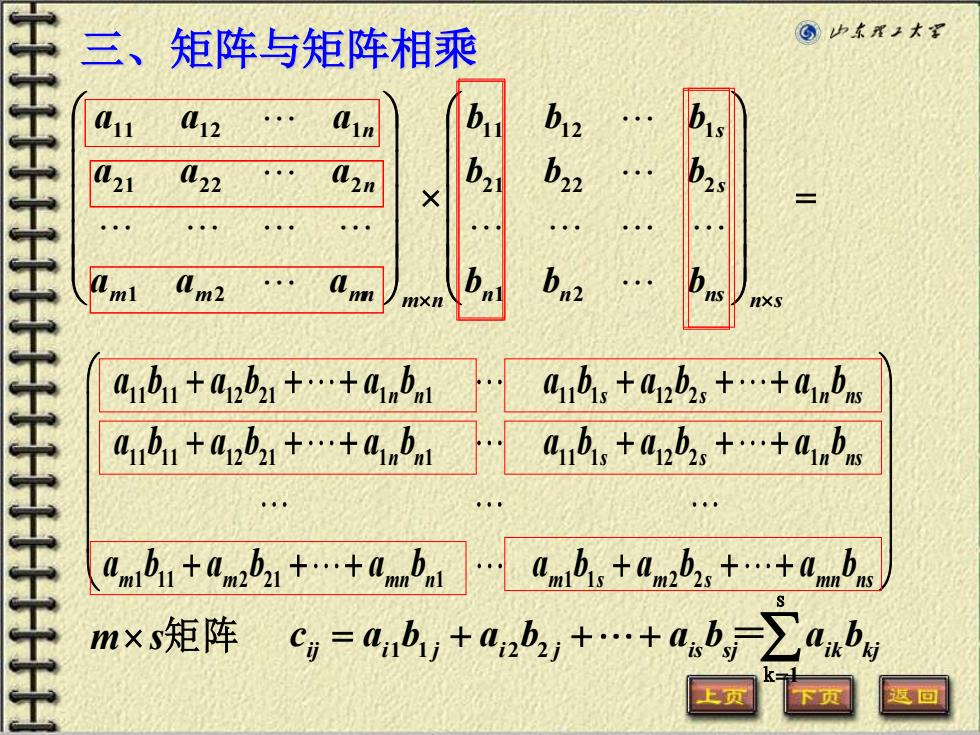
三、 矩阵与矩阵相乘 ©少东理工大罩 12 [n b12 L21 22 b22 m Am2 b b aubu+apx+anb aubis +absa aub+ax+anb a1b,+02b2,+.+a1bnw 0nibi+am,bi+.+anbnL0nib,+0mb,t+anmbe m×s矩阵c=aib,+a2b,+.+ab,-∑ab 上页 区回
m m mn m n n n a a a a a a a a a 1 2 2 1 2 2 2 1 1 1 2 1 = n n ns ns s s b b b b b b b b b 1 2 2 1 2 2 2 1 1 1 2 1 11 11 12 21 1 1 11 1 12 2 1 11 11 12 21 1 1 11 1 12 2 1 1 11 2 21 1 1 1 2 2 n n s s n ns n n s s n ns m m mn n m s m s mn ns a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b a b + + + + + + + + + + + + + + + + + + m s矩阵 三、矩阵与矩阵相乘 = = + + + 1 1 2 2 1 ij i j i j is sj ik kj c a b a b a b a b s k =

©)少东X子大军 1、 定义若A=(a,)mxsB=(b)xn, 规定AB=C=(C)mxn, 其中cy=a,+a,b++ab,∑4bg k (i=1,2,.,m;j=1,2,.,D 注:1)条件左矩阵A的列数等于右矩阵B的行数 2)方法左行右列法—矩阵乘积的元素 等于左矩阵的第行与右矩阵的第列对应元素 乘积的和. 3)结果左行右列一左矩阵A的行数为乘积 C的行数,右矩阵B的列数为乘积C的列数, 王
1、定义 ( ) , AB C c = = ij m n ( ) ( ) , 若 A a B b = = ij m n s s , ij 规定 1 1 2 2 1 ij i j i j is sj ik kj c a b a b a b a b = = + + + s k 其中 = (i m j n = = 1 2 1 2 , ,; , ,) 注: 1)条件 左矩阵A的列数等于右矩阵B的行数 2)方法 C ij c 等于左矩阵 的第 行与右矩阵 的第 列对应元素 左行右列法——矩阵乘积 的元素 A i B j 乘积的和. 3)结果 左行右列——左矩阵A的行数为乘积 C的行数,右矩阵B的列数为乘积C的列数