
@山东理上大 第四节克拉默法则 卫 上页
第四节 克 拉 默 法 则

课前复习余子式与代数余子式 在阶行列式中,把元素所在的第行和第列j 划去后,留下来的n阶行列式叫做元素的余子式, 记作 M前 记A,=(-1)Mp叫做元素的代数余子式. 关于代数余子式的重要性质 含w-暖8 当i=j方 当i≠j 交4-88言 回
课前复习 余子式与代数余子式 记作 . 划去后,留下来的 阶行列式叫做元素 的余子式, ij 在 n 阶行列式中,把元素 a 所在的第 行和第 i 列 j n − 1 ij a Mij( 1) i j A M ij ij + 记 = − , 叫做元素 a 的 ij 代数余子式. 关于代数余子式的重要性质 1 , , 0 , ; n ki kj ij k D i j a A D i j = = = = 当 当 1 , , 0 , ; n ik jk ij k D i j a A D i j = = = = 当 当 1 , 0 , . ij i j i j = = 当 , 当

非齐次与齐次线性方程组的概念 011x1+a12x2+.+41nxn=b1 设线性方程组 21X1+22x2+.+2mn=b2 anx+an2x2++amxn=bn 若常数项勋,b2,.,b不全为零,则称此方程组为非 齐次线性方程组;若常数项b,b2,bn全为零, 此时称方程组为齐次线性方程组 王
+ + + = + + + = + + + = n n nn n n n n n n a x a x a x b a x a x a x b a x a x a x b 1 1 2 2 2 1 1 2 2 2 2 2 1 1 1 1 2 2 1 1 设线性方程组 , , , , 若常数项b1 b2 bn不全为零 则称此方程组为非 齐次线性方程组; , , , , 若常数项b1 b2 bn 全为零 此时称方程组为齐次线性方程组. 非齐次与齐次线性方程组的概念

2、克拉默法则 11火1+012x2++a1nxn=b1 定理如果线性方程组 L21x1+22x2+.+L2mXn=b2 amx1+an2x2++amxn=b 的系数行列式不等于零,即D= 02 ≠0 那么线性方程组有解,并且解可以唯一表示为 x- D
如果线性方程组 11 1 12 2 1 1 21 1 22 2 2 2 1 1 2 2 n n n n n n nn n n a x a x a x b a x a x a x b a x a x a x b + + + = + + + = + + + = 的系数行列式不等于零,即 n n nn n n a a a a a a a a a D 1 2 21 22 2 11 12 1 = 0 2、克拉默法则 定理 那么线性方程组有解,并且解可以唯一表示为 1 2 3 1 2 3 , , , , . n n D D D D x x x x D D D D = = = =
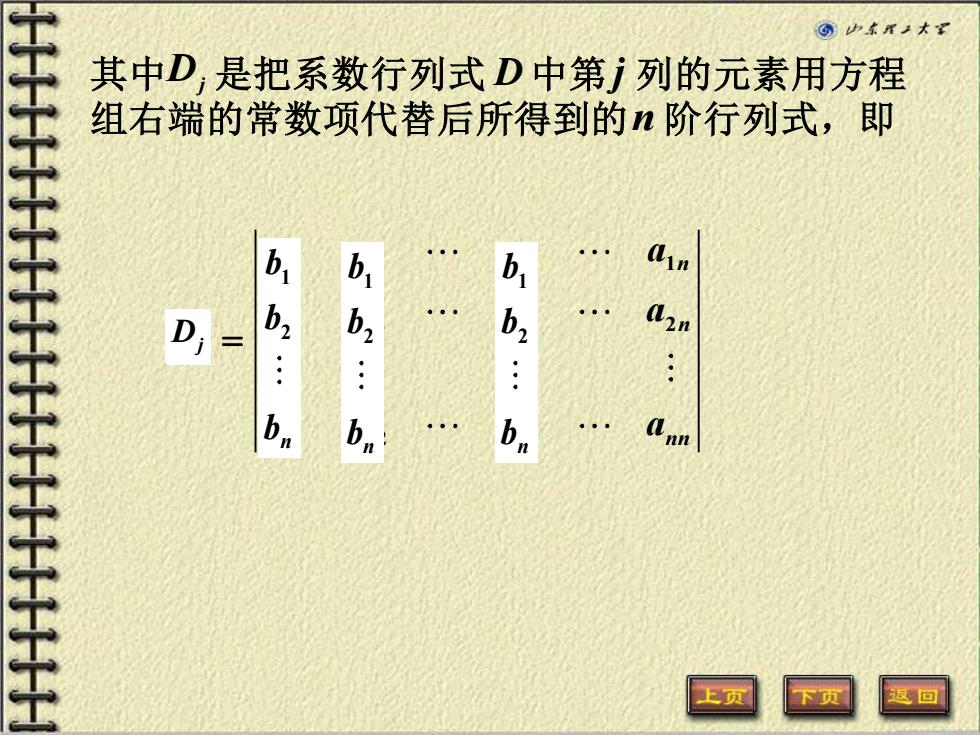
其中D,是把系数行列式D中第列的元素用方程 组右端的常数项代替后所得到的n阶行列式,即 b2 :
其中 是把系数行列式 中第 列的元素用方程 组右端的常数项代替后所得到的 阶行列式,即 Dj D j n 11 12 1 1 21 22 2 2 1 2 j n j n n n nj nn a a a a a a a a D a a a a = 1 2 n b b b 1 2 n b b b 1 2 n b b b D12 Dj