
©中东X王大军 第四章线性方程组 第一节.线性方程组解的判别 第二节.齐次线性方程组 第三节.非齐次线性方程组 上页
第四章 线性方程组 第一节. 线性方程组解的判别 第二节. 齐次线性方程组 第三节. 非齐次线性方程组

柜餐 第一节 线性方程组解的判别 11x1+12x2+.+41mxn=b1 21X1+022X2+.+2mxn=b2 (1) amix1+am2x2++amnxn -bm 11 12 Ain 若记A= 21 L22 ,x= b= aml am2 则上述方程组可写成矩阵方程 Ax=b. 区回
第一节 线性方程组解的判别 设线性方程组 + + + = + + + = + + + = m m mn n m n n n n a x a x a x b a x a x a x b a x a x a x b 1 1 2 2 21 1 22 2 2 2 11 1 12 2 1 1 若记 , 1 2 21 22 2 11 12 1 = m m mn n n a a a a a a a a a A , 2 1 = xn x x x 则上述方程组可写成矩阵方程 Ax = b. , 2 1 = mb b b b (1)

中东翟大写 11 12 称矩阵A=(A,b) 21 L22 02n Am2 为方程组()的增广矩阵。 当b,=0(i=1,2,.,m)时,齐次线性方程组 4X1 012X2 0 421X1 L22X2 十 @nXn 0 (2) am2X2 0 称为方程组(1)的导出组, 或称为(1)对应的齐次线性方程组
称矩阵 为方程组(1)的增广矩阵。 称为方程组(1)的导出组, 或称为(1)对应的齐次线性方程组。 当 0 ( 1,2, , ) i b i m = = 时,齐次线性方程组 11 1 12 2 1 21 1 22 2 2 1 1 2 2 0 0 (2) 0 n n n n m m mn n a x a x a x a x a x a x a x a x a x + + + = + + + = + + + = ( , ) , 2 1 1 2 2 1 2 2 2 1 1 1 2 1 = = m m mn m n n b b b a a a a a a a a a A A b

⑤少本理工大军 对一个方程组进行初等变换,实际上就是对它的增广矩阵 做初等行变换 ERT =(A,b) > S11 S12 Sir S1,r+1 0 S22 S2,r+1 化为行阶 梯形矩阵 0 0. Srr Srn 0 0 0 0 0 r+1 0 0. 0 0 0 .: 0 0 0 0 回
对一个方程组进行初等变换,实际上就是对它的增广矩阵 做初等行变换 ERT A = (A, b) → 11 12 1 1, 1 1 1 22 1 2, 1 2 2 , 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 r r n r r n rr r r rn r r s s s s s t s s s s t s s s t t + + + + ⎯⎯→ 化为行阶 梯形矩阵
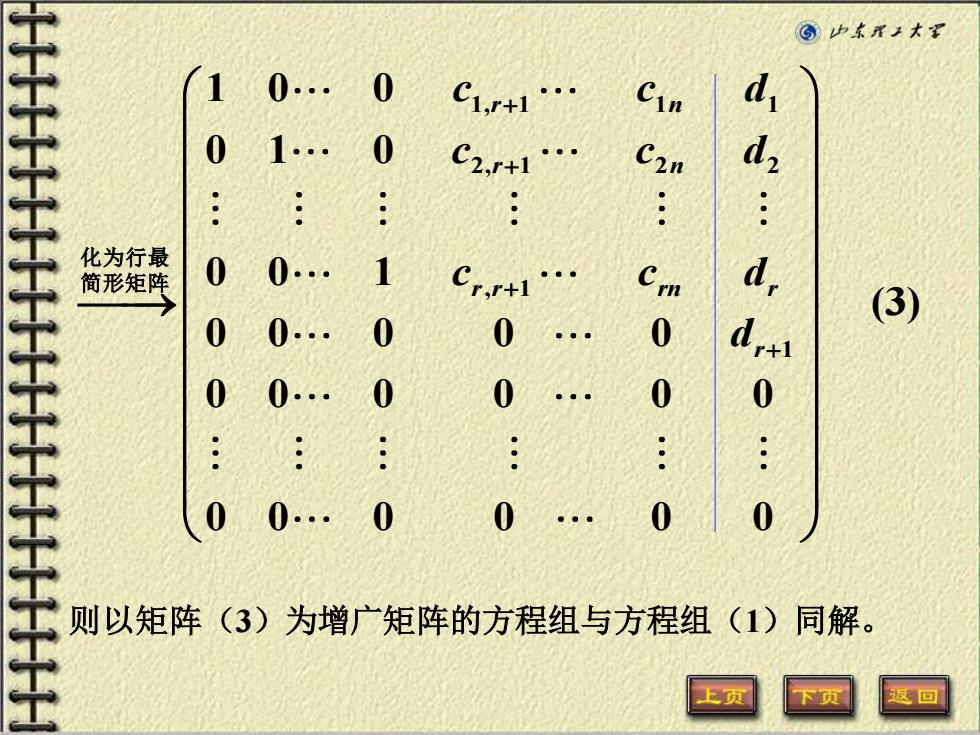
©中东X王大军 1 0 0 C1,+1 Cin d 0 1. 0 C2,r+1 C2n : 化为行最 简形矩阵 0 0. 1 d (3) 0 0 0 0 0 d 0 0. 0 0 0 0 0 0. 0 0 0 则以矩阵(3)为增广矩阵的方程组与方程组(1)同解
则以矩阵(3)为增广矩阵的方程组与方程组(1)同解。 1, 1 1 1 2, 1 2 2 , 1 1 1 0 0 0 1 0 0 0 1 (3) 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 r n r n r r rn r r c c d c c d c c d d + + + + ⎯⎯→ 化为行最 简形矩阵