⑥少本用2大军 第二节阶行列式的性质 上页 下页 返回
第二节 n 阶行列式的性质

⑥少本州3大¥ 课前复习 au 12 3 D= 21 22 l23 =41.23+012023031+014232 -01342031-01i232-01221L3 a31 32 33 =411A1+02A2+03A3 =021A1+42A2+023A3 %11 12 =∑a,4 22 j=1 D =∑(-1(.p =∑(-1)0n12.0pa
11 22 33 12 23 31 13 21 32 = a a a + a a a + a a a 13 22 31 11 23 32 12 21 33 − a a a − a a a − a a a 课前复习 11 12 1 21 22 2 1 2 n n n n nn a a a a a a D a a a = 11 12 13 21 22 23 31 32 33 a a a D a a a a a a = 1 1 1 . n j j j a A = = ( 1 2 ) 1 2 1 2 ( 1) n n p p p p p np a a a = − ( ) 1 2 1 2 1 . n p p p n a a a = − 11 11 12 12 13 13 = + + a A a A a A 21 21 22 22 23 23 = + + a A a A a A

少东大 、行列式按行(列)展开法则 定理1.2.1:行列式等于它的任一行(列)的各元素 与其对应的代数余子式乘积之和,即 》=a+e++aw-a,4 D=a4+ait-.+aa=au4u (i=1,2,.,n) D=a11A11+a12A12+.+a1nA1n(i=1) =2421+22A22+.+2mA2n(i=2) =anlAnl+an24n2++aonAnn
定理1.2.1: 行列式等于它的任一行(列)的各元素 1 n ki ki k a A = = ( i =1, 2, ···, n) D = ai1Ai1 + ai2Ai2 + ··· + ainAin D = a1iA1i+ a2iA2i + ··· + aniAni 与其对应的代数余子式乘积之和, 即 一、行列式按行(列)展开法则 1 n ik ik k a A = = D = a11A11 + a12A12 + ··· + a1nA1n = a21A21 + a22A22 + ··· + a2nA2n = ···= an1An1 + an2An2 + ··· + annAnn ( i =1) ( i =2) ( i =n)

⑥少本用2大¥ 推论 一个n阶行列式,如果其中第i行所有 元素除外都为零,那末这行列式等于,与它的 代数余子式的乘积, 即 D=aA 11 L12 L13 14 例如 l22 L23 D L21 24 0 0 33 0 L41 042 043 044 11 12 L14 =(-103 43321 u22 L24 L41 L42 L44
推论 一个 阶行列式,如果其中第 行所有 元素除 外都为零,那末这行列式等于 与它的 代数余子式的乘积,即 D = aijA.ij n i ij a ij a 41 42 43 44 33 21 22 23 24 11 12 13 14 0 0 0 a a a a a a a a a a a a a D = ( 1) . 41 42 44 21 22 24 11 12 14 33 3 3 a a a a a a a a a a + = − 例如
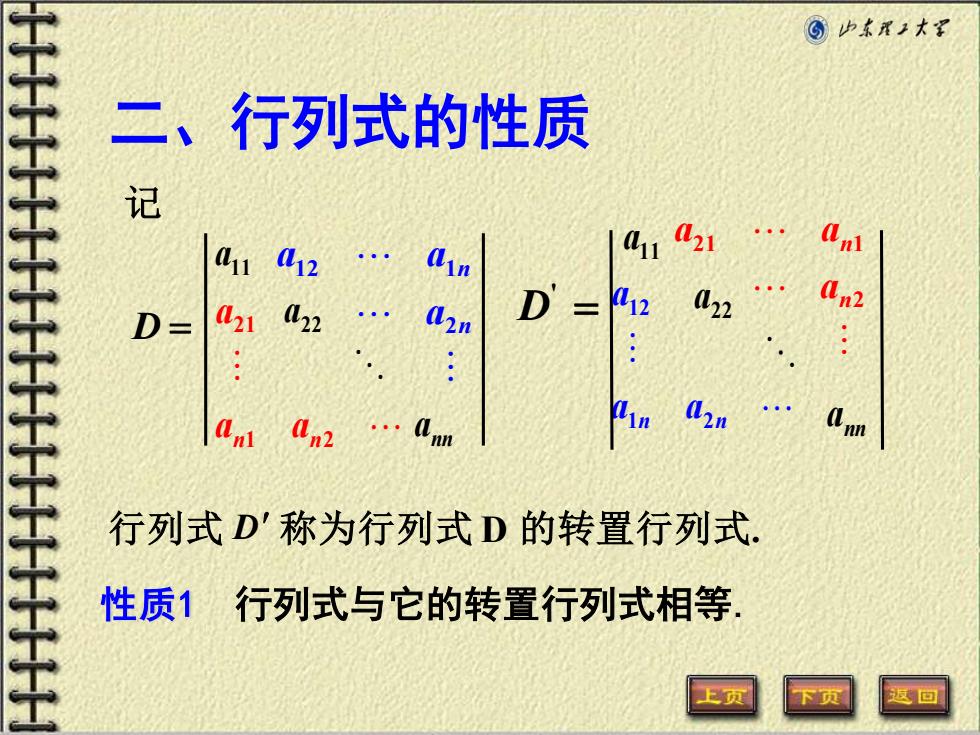
⑥少本1大¥ 二、行列式的性质 记 12 n 41 21 22 D l22 An2 D .Qnn 行列式D'称为行列式D的转置行列式: 性质1行列式与它的转置行列式相等 回
二、行列式的性质 性质1 行列式与它的转置行列式相等. 行列式 D 称为行列式 D 的转置行列式. 记 nn a a a 22 11 n n a a a 2 12 1 1 2 21 n n a a a D = 2 21 1 n n a a a n n a a a 1 2 12 ' D = nn a a a 22 11