
@山东开上大 第三节n阶行列式的计算 上页 返回
第三节 n 阶行列式的计算

一、行列式计算 计算行列式常用方法: 1、利用性质,特别是性质1.2.5把行列式化为上(下)三角 形行列式,从而,较容易的计算行列式的值. 2、利用性质,把行列式化为某一行(列)只有一个非0数 从而,利用定理1.2.1的推论较容易的计算行列式的值. 3、利用递推公式或利用数学归纳法求解, 数值型行列式注意: 1)避免分数运算2)化繁就简3)尽可能用1化零
计算行列式常用方法: 一、行列式计算 1、利用性质,特别是性质1.2.5把行列式化为上(下)三角 形行列式, 从而, 较容易的计算行列式的值. 2、利用性质, 把行列式化为某一行(列)只有一个非0数, 从而,利用定理1.2.1的推论较容易的计算行列式的值. 3、利用递推公式或利用数学归纳法求解. 数值型行列式注意: 1)避免分数运算 2)化繁就简 3)尽可能用1化零

@少本r子大¥ 方法1:化为上三角形行列式: 2 3 -3 3 -7 例1D= 23 0 4 -2 5 1 -14 1-12 3 1 -1 2 -3 0 0 -1 0 ,+3 ⊕0 0 -1 0 2 0 4 -2 0 2 0 4 3 5 7 -14 3 5 7
例1 1 1 2 3 3 3 7 9 2 0 4 2 3 5 7 14 − − − − = − − D 2 1 1 1 2 3 0 0 1 0 3 2 0 4 2 3 5 7 14 − − − + − − r r 方法1:化为上三角形行列式: (− 2) 1 1 2 3 0 0 1 0 0 2 0 4 3 5 7 14 − − − = − 3
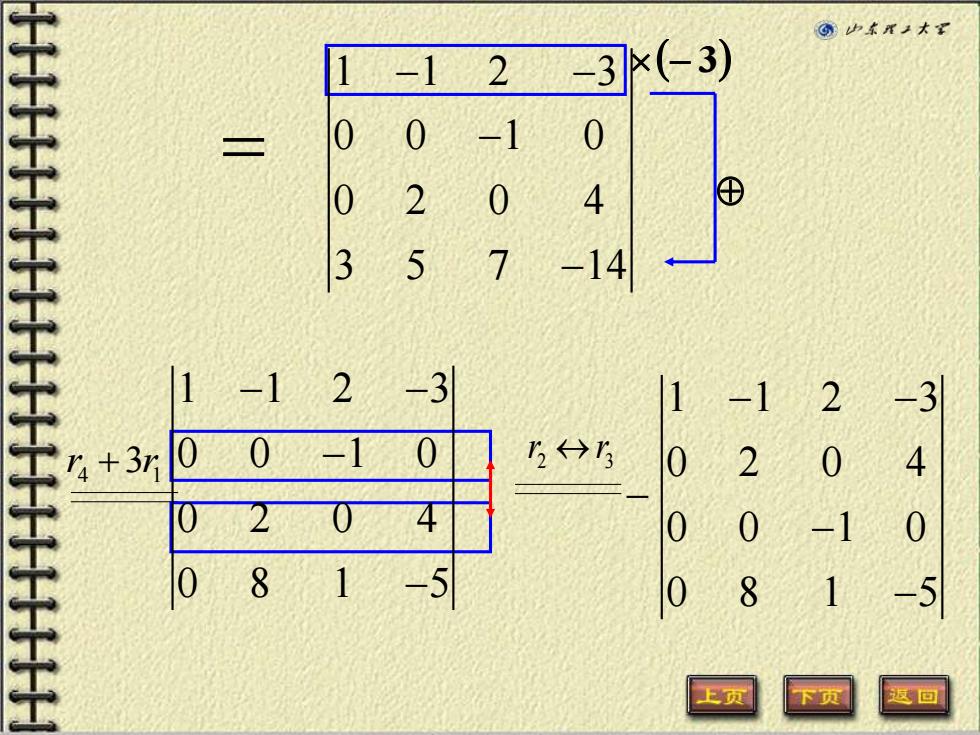
-1 2 -3x-3) 二 0 0 -1 0 0 2 0 4 ⊕ 3 5 7 -14 1-1 2 -3 1 -1 2 -3 +3r 02 0-1 0 2→5 0 2 0 02 0 4 0 0 1 40 08 5 0 8 1 上页
(− 3) 1 1 2 3 0 0 1 0 0 2 0 4 3 5 7 14 − − − − = 4 1 r r +3 1 1 2 3 0 2 0 4 0 0 1 0 0 8 1 5 − − − − − r r 2 3 1 1 2 3 0 0 1 0 0 2 0 4 0 8 1 5 − − − −
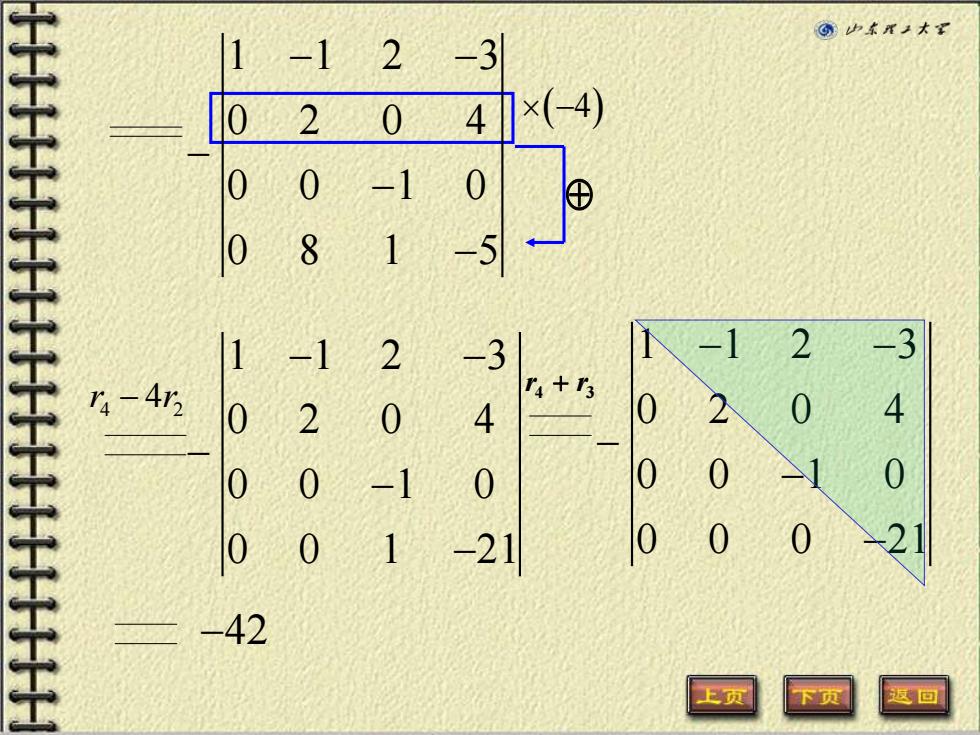
@少本T子大¥ 1 -1 2-3 10204×(4) 0 0 -10 081 -5 1 -1 2 -3 2 4-43 r4+3 0 2 0 4 2 4 0 -1 0 0 0 0 1 -21 0 0 42 上页 返回
4 2 r r − 4 1 1 2 3 0 2 0 4 0 0 1 0 0 8 1 5 − − − − − −( 4) 1 1 2 3 0 2 0 4 0 0 1 0 0 0 1 21 − − − − − 1 1 2 3 0 2 0 4 0 0 1 0 0 0 0 21 − − − − − −42 4 3 r + r