
©山本理上大军 第三草包黨的线性相关性 一、线性组合 二、方程组矩阵向量组的关系 三、 向量组的线性相关性 四、向量组的秩 五、向量空间的维数 返回
四、向量组的秩 一、线性组合 三、 向量组的线性相关性 五、向量空间的维数 二、方程组 矩阵 向量组的关系

©山本理工大军 课前复习 1、定义n个数41,42,.,4n组成的有序数组 a=(a1a2.an 称为一个n维向量,其中a,称为第i个分量(坐标). n维向量写成一行称为行向量, n维向量写成一列称为列向量: 2、几种特殊向量 实向量,复向量,零向量,单位向量,向量同型 士向量相降 工王王
课前复习 1、定义 n个数 a a a 1 2 , , , n 组成的有序数组 = (a a a 1 2 n ) 称为一个n维向量,其中 称为第 个分量(坐标). i a i n维向量写成一行称为行向量, n维向量写成一列称为列向量. 2、几种特殊向量 实向量,复向量,零向量,单位向量,向量同型, 向量相等
©少本理二大 王 4、向量的运算 5、向量组 若干个同维数的列向量(或同维数的行向量)所 组成的集合叫做向量组 6、向量空间 设V为n维非空向量组,且满足 ①对加法封闭 ifa∈'V,B∈V→a+B∈V; ②对数乘封闭 fa∈V,入∈R→a∈V. 那么就称集合V为向量空间!
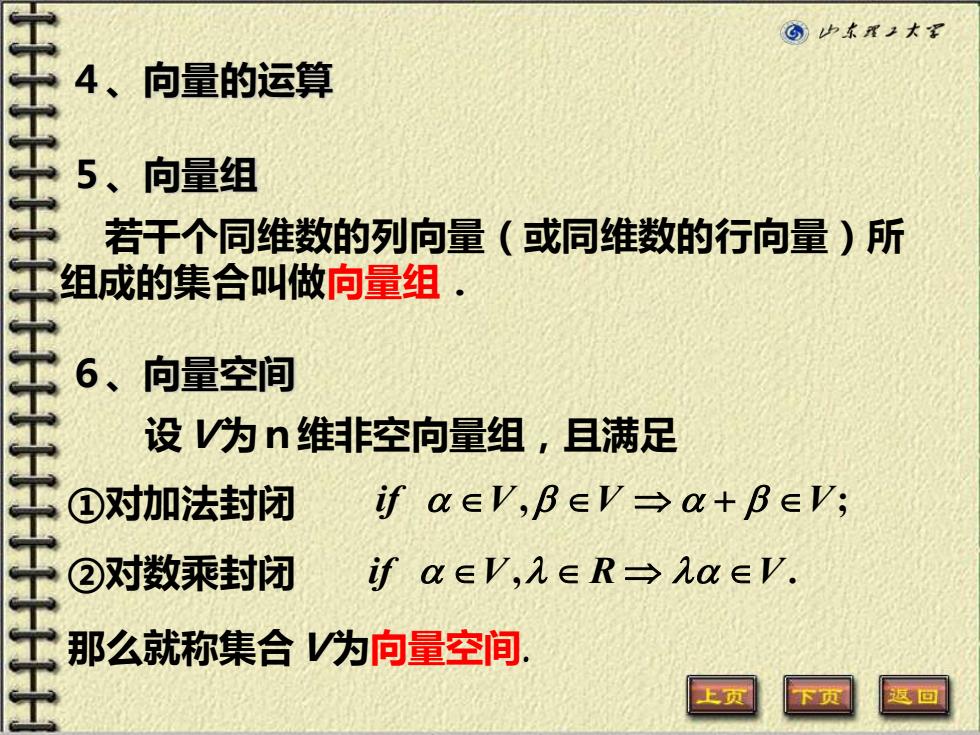
若干个同维数的列向量(或同维数的行向量)所 组成的集合叫做向量组. 5、向量组 if V V V + , ; 6、向量空间 设V为n维非空向量组,且满足 ①对加法封闭 ②对数乘封闭 那么就称集合V为向量空间. if V R V , . 4、向量的运算

©山本理工大军 一、线性组合 1、基本概念 定义2.3.1设向量组A:a1,a2,0n和向量B, 如果存在一组数21,入2,入m使 B=1a1+12a2+.九nm 则向量B是向量组A的一个线性组合,或称向 量B可由向量组A线性表示
1、基本概念 定义2.3.1设向量组 A:1 ,2 , , m 和向量, = 1 1 + 2 2 + m m 则向量 是向量组 A 的一个线性组合,或称向 量 可由向量组 A 线性表示. 如果存在一组数1 ,2 , ,m ,使 一、线性组合

⊙中本理工大军 相关知识点 例1:任一n维向量a=(a,a2.an)都是 n维单位坐标向量组 e=(10.0)62=(01.0), 6=(00.1),的一个线性组合. 显然有 a=a181+a2E2+.+nen 注: ①零向量O是任一向量组的线性组合· O=0a1+0a2+.+0am ②向量组中每一向量都可由该向量组线性表示 a2=0a1+1a2+0a3+.+0am 回
① 零向量O是任一向量组的线性组合. ② 向量组中每一向量都可由该向量组线性表示. 1 2 0 0 0 . O = + + + m ( ) 1 = 1 0 0 , ( ) 2 = 0 1 0 , , (0 0 1) n = , 例1:任一n维向量 = (a a a 1 2 n ) 都是 的一个线性组合. 1 1 2 2 . n n 显然有 = + + + a a a n 维单位坐标向量组 注: 2 1 2 3 = + + + + 0 1 0 0 . m