fx)=4[ inx+ sin3x sin5x sin 7x sinx 3 5 9 (-0<x<+0,x≠0,±π,±2π,.) 说明: 1)根据收敛定理可知, 当x=kπ(k=0,士1,±2,.) 时,级数收敛于-1+=0 2 2)傅氏级数的部分和逼近 f)的情况见右图. 2009年7月27日星期一 11 目录 上页 下页 、返回
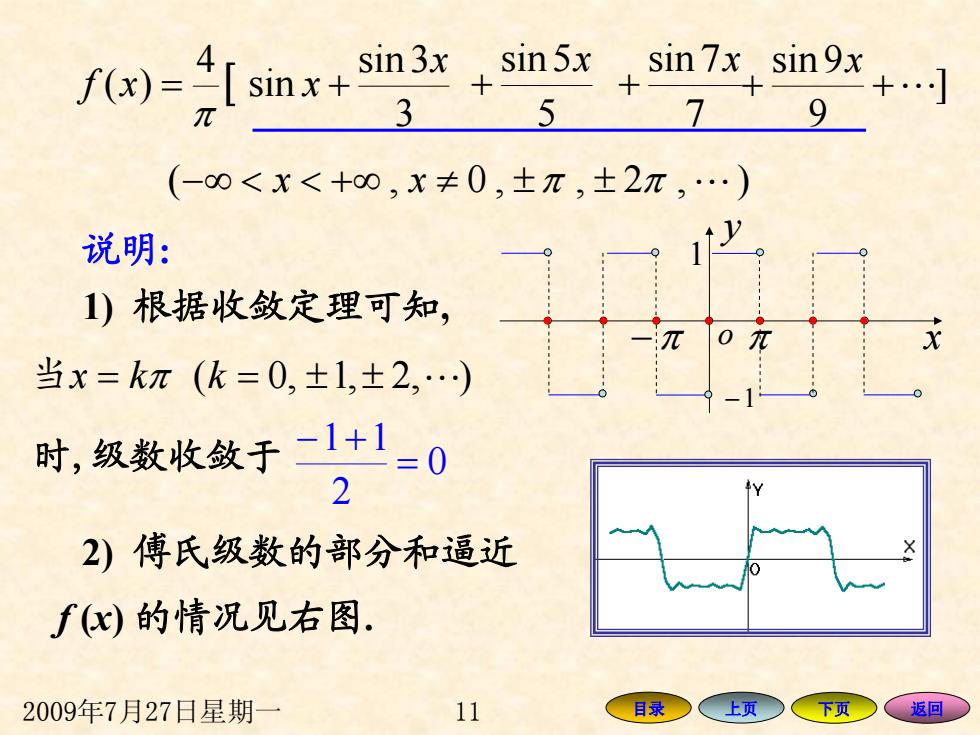
2009年7月27日星期一 11 目录 上页 下页 返回 ( <−∞ < + ∞ xx ≠ ± π ± π "),2,0, 7 7sin x + ] 9 9sin ++ " x 1) 根据收敛定理可知 , 时,级数收敛于 0 2 11 = − + 2) 傅氏级数的部分和逼近 [ 3 3sin sin 4 )( x xf x += π 5 5sin x + o y x − 1 − π 1 π 当 x = kπ k = ± ± "),2,1,0( f (x) 的情况见右图 . 说明 :

例2设fx)是周期为2π的周期函数,它在[-π,π) 上的表达式为 将f)展成傅里叶级数.(由课本例2改编) 矫oxd]月 =f(x)cosnxdx=xconxdx 0 l-cosnπ n2 一元 n2π 2009年7月27日星期一 12 目录 上页 下页 返回
2009年7月27日星期一 12 目录 上页 下页 返回 x −π π o 上的表达式为 y −π π ),[ ⎩ ⎨ ⎧ <≤ − ≤ < = π π x x x xf 0,0 , 0 )( 将 f (x) 展成傅里叶级数 .(由课本 例 2改编) 解: ∫− = π π π d)( xxfa 1 0 ∫− = 0 dcos 1 π π xxnx ∫− = π π π xnxxfan dcos)( 1 ∫− = 0 d 1 π π xx π − π ⎥⎦ ⎤ ⎢⎣ ⎡ = 0 2 2 1 x 2 π −= π − π ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ = + 0 2 cossin1 n nx n nxx π π 2 cos1 n − n = −3 π −2 π 2 π 3 π 例 2 设 f (x) 是周期为 2 π 的周期函数 , 它在

2 202”2k- n=2k (k=1,2,.) b,-是f00 sin-上”.xsinudx-() .(n=1,2,.) +( 2元 cos3x+sm3x)厂sn4 3 2 cos5x+5sim5r)- (-0<x<+0,x≠(2k-1)π,k=0,±1,±2,.) 说明:当x=(2k-1)π时,级数收敛于 0+(-π)_π 2 2 2009年7月27日星期一 13 目录 上页 下页 返回
2009年7月27日星期一 13 目录 上页 下页 返回 n = "),2,1( ∫− = π π π xnxxfbn dsin)( 1 n n 1 )1( + − = k = "),2,1( ⎩ ⎨ ⎧ = n = k −12 ,0 n = 2 k ∫− = 0 dsin 1 π π xnxx f x)( = + − 4 π ( x + cos ) π 2 sin x 2sin x +− 2 1 + ( ) + xx 3sin 3cos π 2 3 2 3 1 4sin x +− 4 1 + ( ) + xx 5sin 5cos π 2 5 2 5 1 − " π π 2 cos1 n n a n − = , 2)12( 2 k − π ( − ∞ < < + ∞ xx ≠ k − π k = ± ± "),2,1,0,)12(, 说明 : 当 x = k − )12( π 时, 级数收敛于 22 π )(0 π −= + −

定义在-元,π上的函数f心)的傅氏级数展开法 f(x),x∈[-π,π] 周期延拓 F) f(x), x∈[-π,π) f(x-2kπ),其它 傅里叶展开 f(x)在[-π,π]上的傅里叶级数 2009年7月27日星期一 14 目录 上页 下页 、返回
2009年7月27日星期一 14 目录 上页 下页 返回 f xx ∈ −π π ],[,)( 周期延拓 F x)( = 傅里叶展开 xf 在 −π π ],[)( 上的傅里叶级数 f x x ∈ −π π ),[ ,)( f x − kπ ,)2( 其它 定义在[– π , π ]上的函数 f (x )的傅氏级数展开法
3将函数四=,元心 展成傅里叶 0≤x≤π 级数.(自学课本例4) 解:将f)延拓成以 2π为周期的函数Fx),则 0元 -dx-dx-xdx 2 =π ,」0 an F(x)cosnxdx()cosd xcosnxdx= xsinnx cosnx n n 2009年7月27日星期一 15 目录 上页 下页 返回
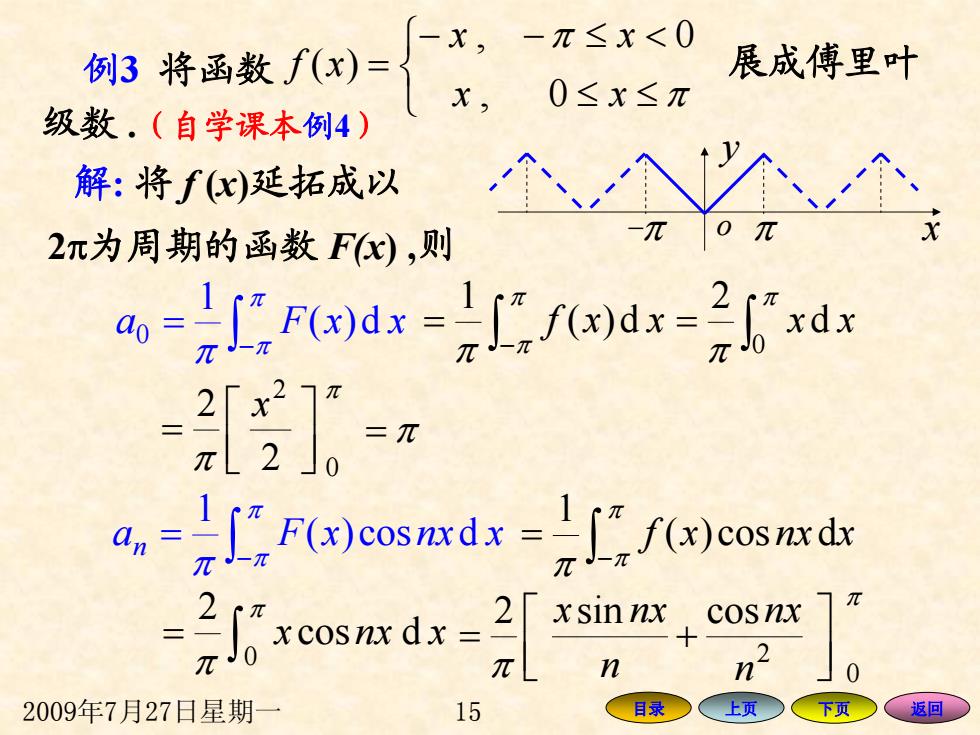
2009年7月27日星期一 15 目录 上页 下页 返回 ⎩ ⎨ ⎧ ≤≤ − − ≤ < = π π xx xx xf 0, , 0 )( 级数 .(自学课本 例 4 ) −π o π y 则 x ∫− = π π π d)( xxFa 1 0 ∫− = π π π d)( xxf 1 ∫ = π π 0 d 2 xx π π 0 2 2 2 ⎥⎦ ⎤ ⎢⎣ ⎡ = x = π ∫− = π π π xnxxFan dcos)( 1 ∫− = π π π dcos)( xnxxf 1 ∫ = π π 0 dcos 2 xnxx π π 0 2 cossin2 ⎥⎦ ⎤ + ⎢⎣ ⎡ = n nx n nxx 解 : 将 f (x )延拓成以 2 π为周期的函数 F(x) , 例3 将函数 展成傅里叶