西安电子科技大学：《复变函数与场论》课程教学课件（讲义，2016）第17讲 复数项级数

复数项级数 Note2: 级数∑IanI的各项都是非负的实数，所以 可用正项级数的审敛法则来判断其收敛性 Note3: 若级数绝对收敛，则∑，收敛，且有： ·[证] Ia.l1o.I ∑1a,收敛=∑a收敛 ∑la,收敛 n= n= →∑a,收敛 ∑1b,收敛→∑b收敛 n= lexu@mail.xidian.edu.cn ● ● 复变函数 11

lexu@mail.xidian.edu.cn 复变函数 11 复数项级数 vNote2：级数 的各项都是非负的实数，所以 可用正项级数的审敛法则来判断其收敛性 vNote3：若级数绝对收敛，则 收敛，且有： § [证] 1 | | n n     1 n n     1 1 | | | | n n n n         1 | n n     |收敛 1 1 | | n n n n a b        |收敛 |收敛 1 n n a     收敛 1 n n b     收敛 1 n n      收敛

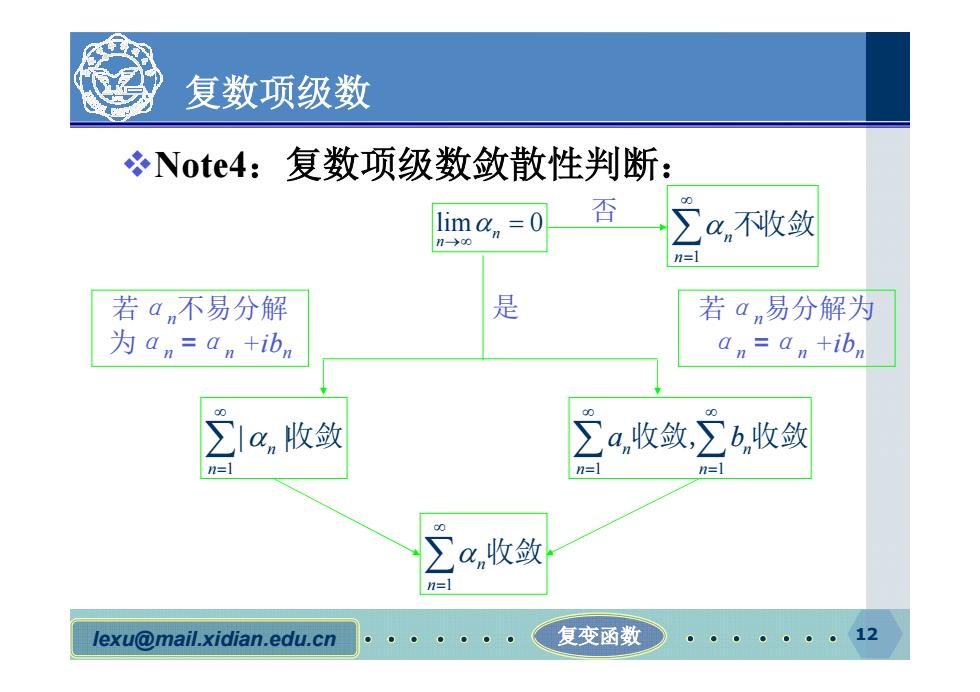
复数项级数 Note4:复数项级数敛散性判断： lima,=0 ∑a不收敛 n=1 若am不易分解 是 若an易分解为 为an=an+ibn an an +ibn ∑lan收敛 ∑a,收敛∑b,收敛 n=1 n=1 a收敛 n=l lexu@mail.xidian.edu.cn 复变函数 。···。。。12

lexu@mail.xidian.edu.cn 复变函数 12 复数项级数 vNote4：复数项级数敛散性判断： lim 0 n n    否 1 1 n n n n a b       收敛, 收敛 1 | | n n     收敛 若α n不易分解 为α n =α n +ibn 若α n易分解为 α n =α n +ibn 是 1 n n     收敛 1 n n     不收敛