
复数项级数 Notel:以复数序列表示复数平面上的点 集,则点列{z收敛于z的定义为 》任给z的一个领域,相应地有一个正整 数N,使得n>N时,zn在这个领域内 Note2:对比实数序列定义及性质知两个收 敛序列的四则运算结果仍收敛,且 其极限为相应极限的四则运算 lexu@mail.xidian.edu.cn 复变函数 6
lexu@mail.xidian.edu.cn 复变函数 6 复数项级数 vNote1:以复数序列表示复数平面上的点 集,则点列{zn}收敛于z0的定义为 »任给z0的一个领域,相应地有一个正整 数N,使得n>N时, zn在这个领域内 vNote2:对比实数序列定义及性质知两个收 敛序列的四则运算结果仍收敛,且 其极限为相应极限的四则运算

复数项级数 冬复数项级数 ▣设{am}={an+ibm(n=L,2.)为一复数列,则: ·无穷级数:】 a=+%++ ·级数的部分和: Sn=a1+02+…+Cn ·如果部分和数列{s}收敛,则级数收敛 ·部分和数列的极限成为级数的和,记作 lim s =s ·若部分和数列{s}不收敛,则级数发散 lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn 复变函数 7 复数项级数 v复数项级数 § 设{αn}={an+ibn}(n=1,2,…)为一复数列,则: • 无穷级数: • 级数的部分和: § 如果部分和数列{sn}收敛,则级数收敛 § 部分和数列的极限成为级数的和,记作 § 若部分和数列{sn}不收敛,则级数发散 1 2 1 n n n n n 1 2 s lim n n s s
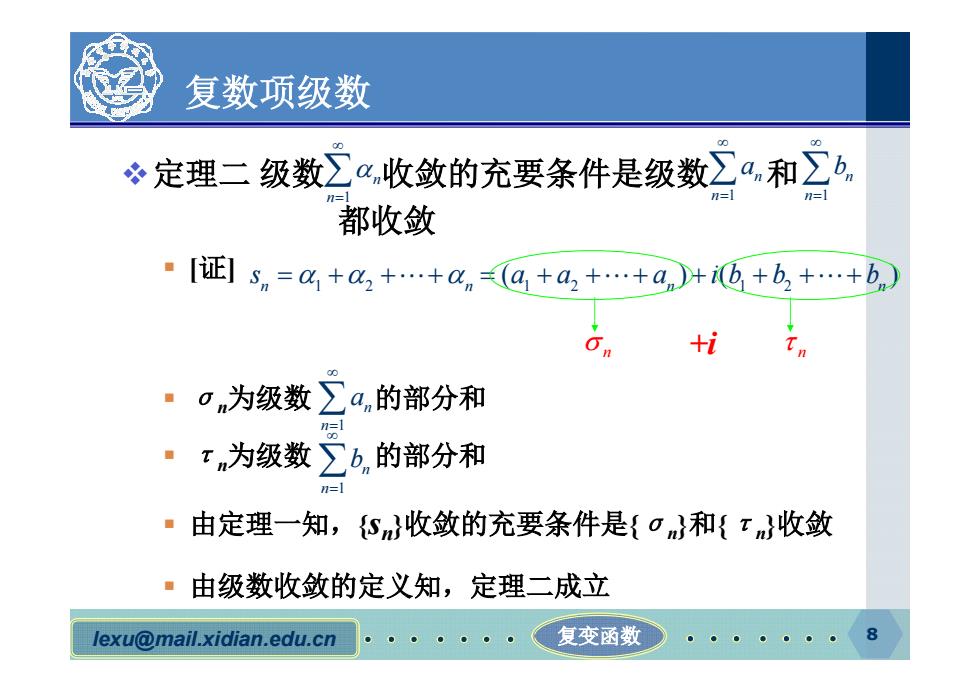
复数项级数 ÷定理二级数∑α,收敛的充要条件是级数∑a,和∑b。 都收敛 ·[证]sn=a4+4,+…+an(a+a42+…+a)+i6+b,+…+bn +i 0n为级数 2a,的部分和 tm为级数∑b,的部分和 由定理一知,{S收敛的充要条件是{om}和{tm收敛 ·由级数收敛的定义知,定理二成立 lexu@mail.xidian.edu.cn 复变函数 8
lexu@mail.xidian.edu.cn 复变函数 8 复数项级数 v定理二 级数 收敛的充要条件是级数 和 都收敛 § [证] § σn为级数 的部分和 § τn为级数 的部分和 § 由定理一知,{sn}收敛的充要条件是{σn}和{τn}收敛 § 由级数收敛的定义知,定理二成立 1 n n 1 n n a 1 n n b n n 1 2 s 1 2 1 2 ( ) ( ) n n a a a i b b b n n +i 1 n n a 1 n n b

复数项级数 Note1:定理二将复数项级数的审敛问题转化为两 个实数项级数的审敛问题 Note2: 复数项级数∑&n收敛的必要条件是lima,=0 2a收敛 →lima,=0 n→00 — →lima=0 1300 2,收敛 →limb=0 n00 lexu@mail.xidian.edu.cn 复变函数
lexu@mail.xidian.edu.cn 复变函数 9 复数项级数 vNote1:定理二将复数项级数的审敛问题转化为两 个实数项级数的审敛问题 vNote2:复数项级数 收敛的必要条件是 1 n n lim 0 n n 1 1 1 n n n n n n a b 收敛 收敛 收敛 lim 0 n n a lim 0 n n b lim 0 n n
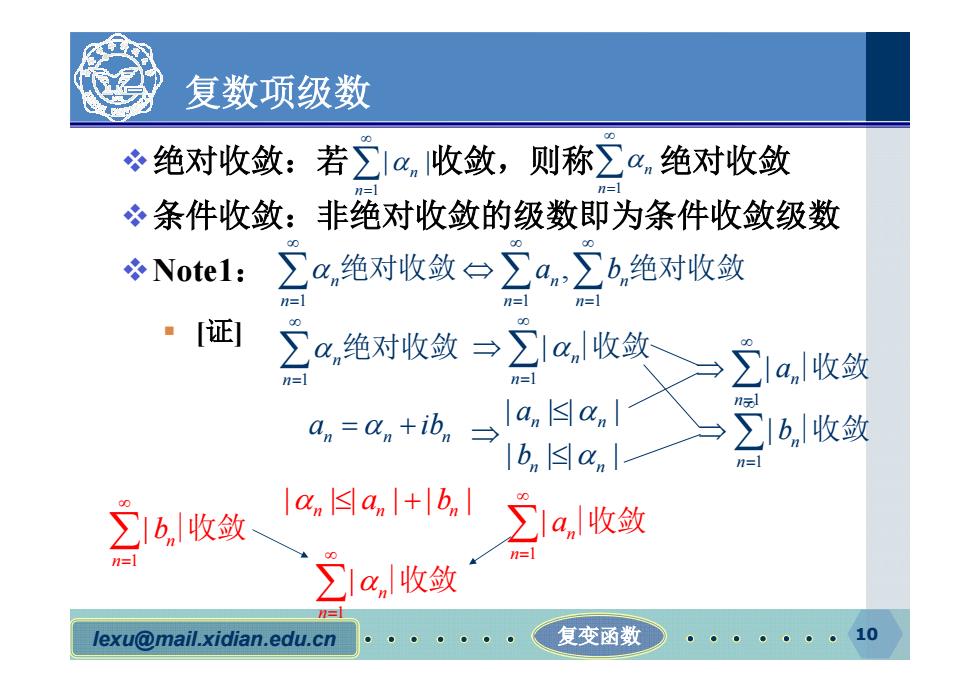
复数项级数 必绝对收敛: 若∑1a,收敛,则称∑a,绝对收敛 条件收敛:非绝对收敛的级数即为条件收敛级数 Notel: 立a,绝对收敛台立46,绝对收敛 [证] 立4绝对收敛→2a收签 n=1 2 a,收敛 lb,a1 ∑b,收敛 la s a+b ∑1b,收敛 ∑a收敛 n ∑1a收敛 lexu@mail.xidian.edu.cn 复变函数 10
lexu@mail.xidian.edu.cn 复变函数 10 复数项级数 v绝对收敛:若 收敛,则称 绝对收敛 v条件收敛:非绝对收敛的级数即为条件收敛级数 vNote1: § [证] 1 | | n n 1 n n 1 1 1 , n n n n n n a b 绝对收敛 绝对收敛 1 n n 绝对收敛 1 | n n |收敛 | | | | | | | | n n n n a b n n n a ib 1 | n n a |收敛 1 | n n b |收敛 | | | | | | n n n a b 1 | n n a |收敛 1 | n n b |收敛 1 | n n |收敛