
东液园 一、问题的提出 z=f(x,y) 1.曲顶柱体的体积 给定曲顶柱体: 底:xoy面上的闭区域D 顶:连续曲面z=∫(x,y)≥0 侧面:以D的边界为准线,母线平行于z轴的柱面 求其体积 问题:如何计算曲顶柱体的体积?
山东农业大学 高等数学 主讲人:苏本堂 问题: 如何计算曲顶柱体的体积? 一、问题的提出 1.曲顶柱体的体积 给定曲顶柱体: 底: xoy 面上的闭区域 D 顶: 连续曲面 侧面:以 D 的边界为准线 , 母线平行于 z 轴的柱面 求其体积. D

山东农业大 高等数学 本 问题:如何计算曲顶柱体的体积? =f(x,y 柱体体积=底面积关高 柱体体积=? 特点:平顶. 特点:曲顶 解决问题的思路:类似定积分解决问题的思想: 分割,近似,求和, 取极限
山东农业大学 高等数学 主讲人:苏本堂 柱体体积=底面积×高 特点:平顶. 柱体体积=? 特点:曲顶. z = f (x, y) D 问题: 如何计算曲顶柱体的体积? “分割, 近似, 求和, 取极限” 解决问题的思路: 类似定积分解决问题的思想: ×
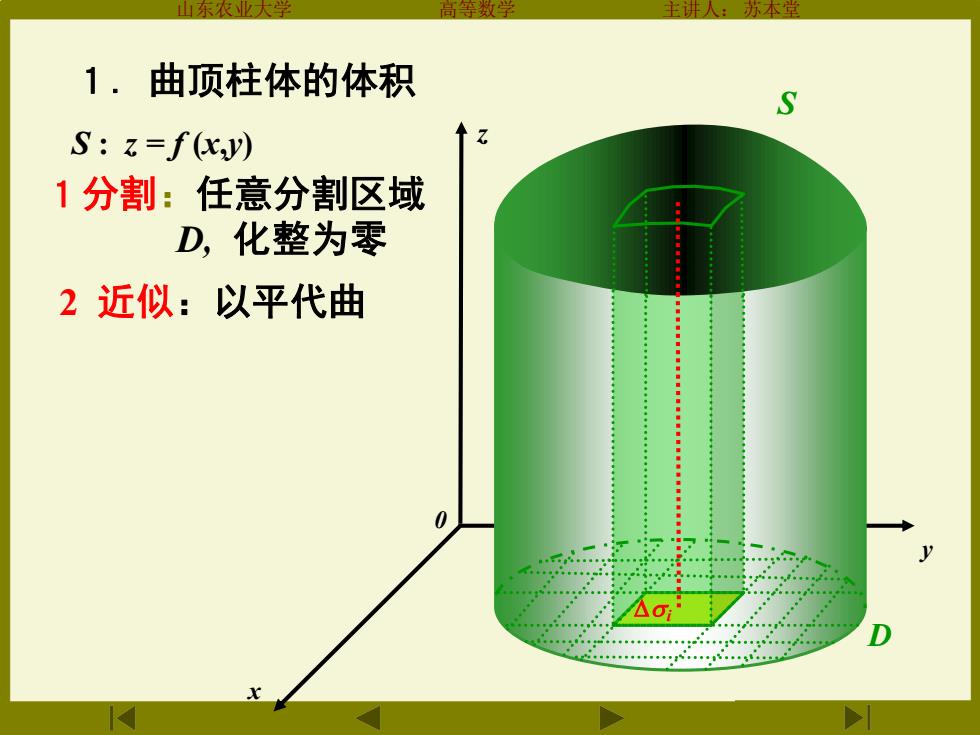
1.曲顶柱体的体积 S S:z=f(xy) 1分割:任意分割区域 D,化整为零 2近似:以平代曲 0 河
山东农业大学 高等数学 主讲人:苏本堂 x 0 z y D S S : z = f (x,y) 1分割:任意分割区域 D, 化整为零 2 近似:以平代曲 1. 曲顶柱体的体积 i

山东农业大 主讲人:本堂 1.曲顶柱体的体积 S:z=f(xy) 1分割:任意分割区域 D,化整为零 2近似:以平代曲 △V≈f(5,7,)△o 3求和:V≈∑f5,)△o 0 .△g
山东农业大学 高等数学 主讲人:苏本堂 x 0 z y D S : z = f (x,y) i i i i V f ( , ) 3 求和: = n i i i i V f 1 ( , ) 2 近似:以平代曲 1 分割:任意分割区域 D, 化整为零 . i 1. 曲顶柱体的体积
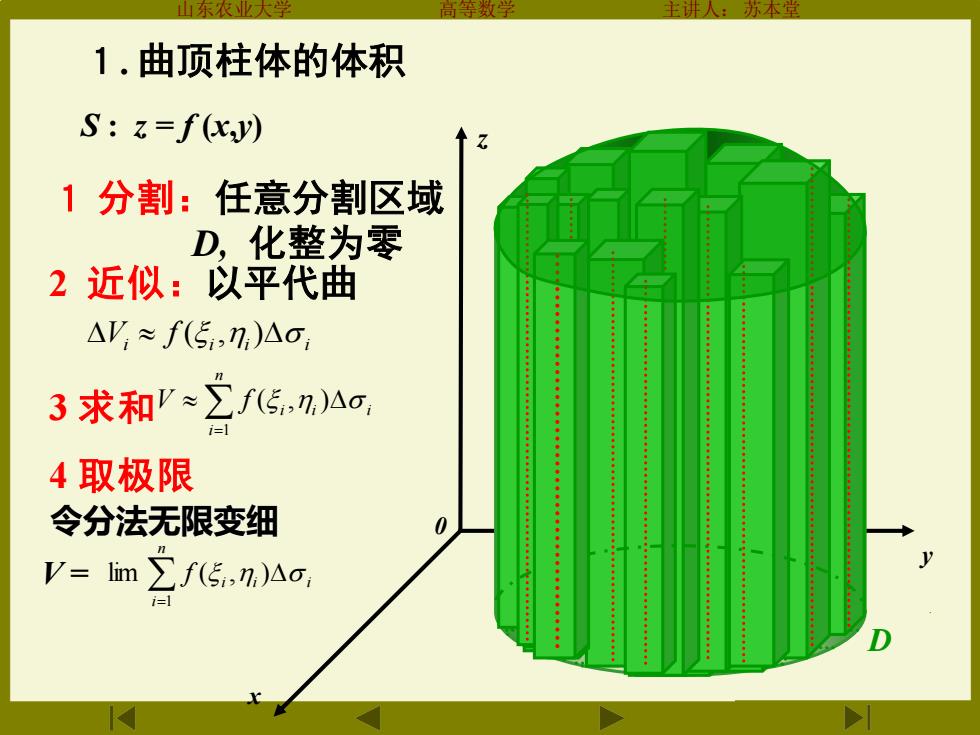
东液 1.曲顶柱体的体积 S:z=f(xy) 1分割:任意分割区域 D,化整为零 2近似:以平代曲 △V≈f(5,7,)△o 3求和'≈∑f,n)△o 4取极限 令分法无限变细 V=lim∑f5,n,)△o, i=1
山东农业大学 高等数学 主讲人:苏本堂 x 0 z y D S : z = f (x,y) i i i i V f ( , ) 3 求和 = n i i i i V f 1 ( , ) 4 取极限 令分法无限变细 i 2 近似:以平代曲 1 分割:任意分割区域 D, 化整为零 . = n i i i i f 1 V = lim ( , ) 1. 曲顶柱体的体积